Каноническое уравнение имеет вид 
,
где 
и 
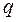- это параметры параболоида, 
; 
,
Строим методом сечений.
1) Находим линию пересечения с плоскостью 
.
Решаем систему уравнений
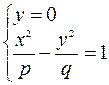
- это уравнение параболы, симметричной относительно оси 
.
2) Находим линию пересечения с плоскостью 
.
Решаем систему уравнений
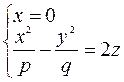
- это уравнение параболы,
симметричной относительно оси .
3) Находим линии пересечения с плоскостями, параллельными
плоскости 
.
а) Решаем систему уравнений
- это уравнение гиперболы, у которой
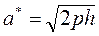- действительная полуось, а 
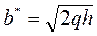- мнимая полуось.
б) Решаем систему уравнений
(знак левой части изменился, так как 
по условию)
- это уравнение гиперболы, у которой 
- действительная полуось, а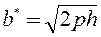 
- мнимая полуось.
4) Находим линию пересечения с плоскостью .
Решаем систему уравнений
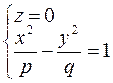
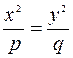- это уравнение двух прямых, проходящих через точку 
.
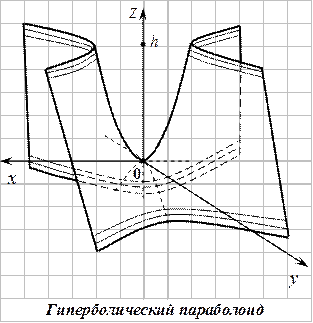
Гиперболический параболоид – это поверхность, имеющая вид седла.
Конус второго порядка
Каноническое уравнение имеет вид 
Строим методом сечений.
1) Находим линию пересечения с плоскостью 
.
Решаем систему уравнений
- это уравнение точки 
.
2) Находим линии пересечения с плоскостями параллельными 
.
Решаем систему уравнений
- это уравнение эллипса
с полуосями 
и 
.
3) Находим линию пересечения с плоскостью 
.
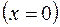Решаем систему уравнений
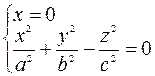
- это уравнение двух прямых, проходящих через начало координат.
4) Находим линию пересечения с плоскостью 
.
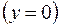Решаем систему уравнений
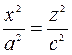- это уравнение двух прямых, проходящих через начало координат.
Цилиндрические поверхности
Задаются уравнениями:
; образующая параллельна оси ;
; образующая параллельна оси 
;
; образующая параллельна оси 
;
1. Эллиптический цилиндр
направляющая - эллипс,
образующая параллельна оси
2. Параболический цилиндр
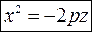
направляющая - парабола,
образующая параллельна оси
3. Гиперболический цилиндр
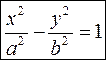
направляющая - гипербола,
образующая параллельна оси .
Пример 1. Построить поверхность
заданную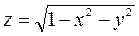 
.
¦ Из уравнения следует, что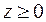 
. Возведем обе части уравнения в квадрат 
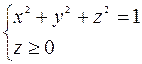
полусфера,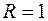 
,
с центром в точке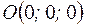 
. ?
Пример 2. Построить тело, ограниченное поверхностями
.
¦ Определим вид поверхностей.
- параболический цилиндр;
- плоскость;
- координатные плоскости. ?
ЛИТЕРАТУРА
1. Шипачев В.С. Основы высшей математики [Текст]: Учебное пособие / В.С.Шипачев, 2002. - 479с.
2. Ильин В.А. Аналитическая геометрия [Текст]: Учебник / В.А.Ильин, Э.Г. Позняк, 2002. - 240с.
3. Зимина О.В. Линейная алгебра и аналитическая геометрия [Текст]: Учебный комплекс: Учебное пособие / О.В.Зимина; Под ред. А.И.Кириллова, 2000. – 328с.
4. Сборник задач по математике для втузов. В 4-х ч [Текст]: Учебное пособие для втузов. Ч.1 / Ред. А.В.Ефимов, Ред. А.С.Поспелов, 2003. – 288с.
5. Данко П.Е. Высшая математика в упражнениях и задачах [Текст]: Учебное пособие в 2-х ч. Ч.2 / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова, 2005. – 404с.
6. Руководство к решению задач по высшей математике [Текст]: Учебное пособие в 2-х ч. Ч.1 /Е.И.Гурский, В.П.Домашов, В.К.Кравцов, А.П.Сильванович; Под общ. Ред. Е.И.Гурского, 1989. – 349 с.
