1. Находим 
: - если 
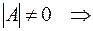существует 
;
- если 
не существует .
2. Находим транспонированную матрицу 
.
3. Находим присоединенную матрицу. Она состоит из алгебраических дополнений элементов матрицы .
Обозначение присоединенной матрицы: или 
, или 
, или 
.
4. Находим обратную матрицу: 
.
5. Делаем проверку: 
или 
.
Пример.Найти матрицу, обратную данной:  .
| ||||
| ¦ 1) | 
| существует  .
| 2) |  .
|
| 3) |  .
| |||
| 4) |  .
| |||
| 5) |
Проверка: (выполнить самостоятельно).?
|
Вычисление обратной матрицы методом элементарных преобразований
Элементарные преобразования матрицы.
1. Перестановка строк (столбцов).
2. Умножение строки (столбца) на число 
.
3. Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на любое число.
Чтобы найти матрицу, обратную данной, делаем следующее:
- для матрицы 
строим прямоугольную матрицу 
,
приписывая справа единичную матрицу;
- с помощью элементарных преобразований приводим матрицу
к виду 
.
Тогда 
.
Эквивалентные матрицы обозначаются 
.
Пример. Найти матрицу, обратную данной: 
.
~( первую строку матрицы умножили на 
) ~ 
~ 
~ 
~
Следовательно, 
.
Проверка: 
. ?
§ 5. Системы m линейных уравнений с n переменными
Основные понятия
Системы m линейных уравнений с n переменными имеют вид:
 (1)
|
где 
, 
- 
- произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами.
Решением системы называется совокупность 
чисел 
, при подстановке которых все уравнения системы обращаются в верные равенства.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы называются равносильными (или эквивалентными) если они имеют одно и то же множество решений.
Равносильность систем не нарушается при следующих элементарных преобразованиях:
1) перемена местами уравнений;
2) умножение обеих частей уравнения на число ;
3) удаление из системы уравнения 
;
4) прибавление к обеим частям какого - либо уравнения соответствующих частей другого уравнения этой же системы, предварительно умноженных на любое число.
Запишем матрицы:
, 
, 
.
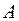- матрица системы, состоящая из коэффициентов при переменных,
- матрица-столбец переменных,
- матрица- столбец свободных членов.
Так как число столбцов матрицы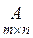 
равно числу строк матрицы 
, то их произведение есть матрица-столбец:
 .
|
Элементами полученной матрицы являются левые части уравнений системы (1).
На основании определения равенства матриц систему (1) можно записать в следующем виде: 
- это матричный вид системы.
Матрица системы, дополненная столбцом свободных членов, называется расширенной матрицей.
| - расширенная матрица системы (1) |
5.2. Системы n линейных уравнений с n переменными.
