1. Возведение в степень возможно только для квадратных матриц.
 .
.
Например,  .
.
Свойства:
1) 
| 2) 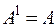
| 3) 
| 4) 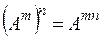
|
2. Транспонирование матрицы – это переход от матрицы  к матрице
к матрице  , при котором строки и столбцы меняются местами с сохранением порядка.
, при котором строки и столбцы меняются местами с сохранением порядка.
Если 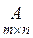 , то
, то  .
.
Например, 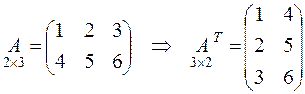 .
.
Свойства:
1) 
| 2) 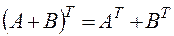
| 3) 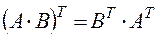
|
Определители
Основные понятия
Квадратной матрице 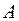
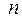 - го порядка соответствует число, называемое определителем (или детерминантом).
- го порядка соответствует число, называемое определителем (или детерминантом).
Обозначается определитель:  ;
; 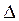 или
или 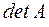 .
.
Если 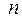 = 1 = 1  , то , то
| 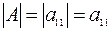
| - определитель 1-го порядка. | |
Если 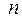 = 2 = 2 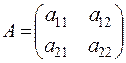 , то , то
| 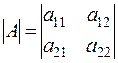
| - определитель 2-го порядка. | |



 Схема вычисления:
Схема вычисления:
Например,  .
.
Если 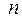 = 3 = 3
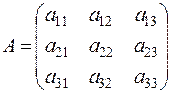 , то , то
|

| - определитель 3-го порядка. |
Определитель третьего порядка можно вычислять по правилу треугольников (правилу Саррюса).
Схема вычисления:

Например, 
Свойства определителей
1. Определитель не изменится, если его строки заменить столбцами и наоборот.
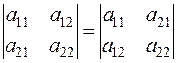 .
.
Будем называть строки и столбцы рядами определителя.
2. При перестановке двух параллельных рядов определитель меняет знак.
3. Определитель, имеющий два одинаковых ряда, равен нулю.
4. Общий множитель элементов какого-либо ряда можно выносить за знак определителя.
5. Если элементы какого-либо ряда представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей:
 .
.
6. Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, предварительно умноженные на любое число 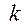 :
:
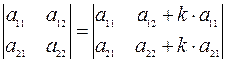 .
.
Определение. Минором некоторого элемента 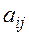 определителя
определителя 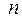 - го порядка называется определитель (
- го порядка называется определитель (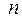 - 1) – го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых стоит этот элемент.
- 1) – го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых стоит этот элемент.
Обозначается: 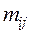 .
.


 Если
Если  , то
, то 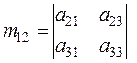 .
.
Определение. Алгебраическим дополнением элемента 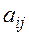 называется его минор, умноженный на
называется его минор, умноженный на 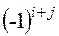 .
.
Обозначается:  .
.
7. ( Разложение определителя по элементам некоторого ряда).
Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения:
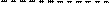
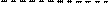
 .
.
Например,



Определители высоких порядков вычисляем, применяя свойство 7. При вычислении определителей третьего и более высокого порядка удобно пользоваться свойством 6. Покажем на примере вычисления определителя третьего порядка.
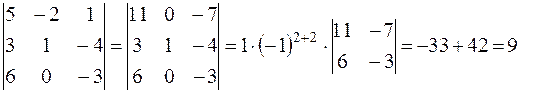
Первую строку заменили суммой ее со второй, предварительно умноженной на число 2.
Обратная матрица
Основные понятия
Для каждого числа 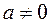 существует обратное ему число
существует обратное ему число  , причем
, причем 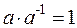 .
.
Для квадратных матриц вводится аналогичное понятие.
Определение. Матрица  называется обратной матрице
называется обратной матрице  , если выполняется равенство:
, если выполняется равенство: 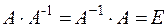 .
.
Условием существования обратной матрицы является требование:  .
.
Определение. Если  , то матрица
, то матрица 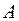 называется невырожденной; если
называется невырожденной; если  , то матрица
, то матрица 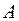 называется вырожденной.
называется вырожденной.






