Каноническое уравнение имеет вид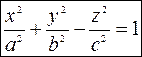 
Строим методом сечений.
1) Находим линию пересечения с плоскостью 
.
Решаем систему уравнений 
- это уравнение эллипса с полуосями 
и 
.
2) Находим линии пересечения с плоскостями, параллельными плоскости : 
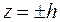
Решаем систему уравнений
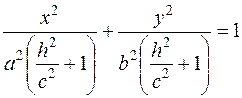
- это уравнение эллипса с полуосям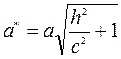и 
и 
.
3) Находим линию пересечения с плоскостью 
.
Решаем систему уравнений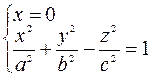 
- это уравнение гиперболы,
где - действительная полуось, а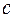 
- мнимая полуось.
4) Находим линию пересечения с плоскостью 
.
Решаем систему уравнений
- это уравнение гиперболы.
- действительная полуось, а 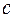- мнимая полуось.
Однополостный гиперболоид – это бесконечная труба, которая бесконечно расширяется по мере удаления от плоскости .
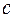, , - это полуоси гиперболоида. Полуось 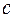увидим, если построим основной прямоугольник какой-либо из гипербол.
Двуполостный гиперболоид.
Каноническое уравнение имеет вид 
.
1) Находим линию пересечения с плоскостью .
Решаем систему уравнений
 
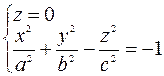
| - это уравнение мнимого эллипса. |
Следовательно, с плоскостью нет общих точек.
2) Находим линии пересечения с плоскостями, параллельными плоскости :
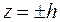
а) Решаем систему уравнений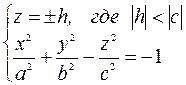 
- это уравнение мнимого эллипса, так как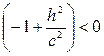 
.
б) Решаем систему уравнений
.
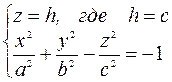
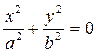Получим точки 
и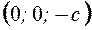 
.
в) Решаем систему уравнений
;
- это уравнение эллипса, с полуосям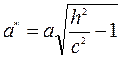и 
и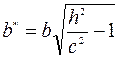 
.
2) Находим линию пересечения с плоскостью .
Решаем систему уравнений 
- это уравнение гиперболы,
где 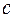-действительная полуось,
а - мнимая полуось.
3) Находим линию пересечения с плоскостью .
Решаем систему уравнений
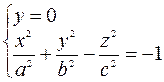
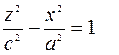- это уравнение гиперболы,
где 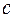- действительная полуось, а - мнимая полуось.
Двуполостный гиперболоид - это две чаши с вершинами в точках 
и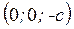 
, которые бесконечно расширяются по мере удаления от плоскости .
, и 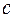- полуоси гиперболы. Полуоси и увидим, если построим основные прямоугольники обеих гипербол.
Эллиптический параболоид.
Каноническое уравнение имеет вид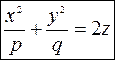 
,
где 
и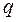 
это параметры параболоида, 
; 
,
Строим методом сечений.
1) Находим линию пересечения с плоскостью .
Решаем систему уравнений
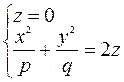
- это уравнение точки 
.
2) Находим линии пересечения с плоскостями, параллельными
плоскости .
Решаем систему уравнений
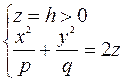
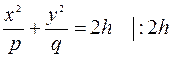
- это уравнение эллипса с полуосями 
и 
.
При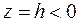 
получим уравнение мнимого эллипса.
3) Находим линию пересечения с плоскостью .
Решаем систему уравнений
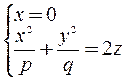
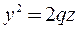
- это уравнение параболы симметричной относительно оси 
.
4) Аналогично найдем линию пересечения с плоскостью .
Это будет парабола 
симметричная относительно оси .
Если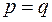 
, то получаем параболоид вращения.
