Системы n линейных уравнений с n переменными имеют вид:
 (2) (2)
|
Матрица  такой системы является квадратной, и ей соответствует определитель
такой системы является квадратной, и ей соответствует определитель  - го порядка
- го порядка 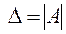 , называемый главным определителем системы. Решение системы (2), в случае
, называемый главным определителем системы. Решение системы (2), в случае  , может быть найдено по формулам Крамера.
, может быть найдено по формулам Крамера.
 ,
,
где  - вспомогательные определители системы.
- вспомогательные определители системы.
Главный определитель системы состоит из коэффициентов при переменных, а вспомогательные составляют из главного, заменяя столбец коэффициентов (при соответствующей переменной) столбцом свободных членов.
Если  , то система имеет единственное решение;
, то система имеет единственное решение;
если  , то система имеет бесконечно много решений;
, то система имеет бесконечно много решений;
если  и какой-либо из вспомогательных определителей не равен нулю, то система не имеет решений (или имеет
и какой-либо из вспомогательных определителей не равен нулю, то система не имеет решений (или имеет  (пустое множество) решений).
(пустое множество) решений).
Метод обратной матрицы
Запишем систему (2) в матричном виде и решим матричное уравнение:


Матричное уравнение может иметь и другой вид: 

Метод Гаусса
Одним из наиболее универсальных методов решения алгебраических систем является метод Гаусса, состоящий в последовательном исключении переменных.
Пусть дана система уравнений:

На первом этапе (прямой ход) систему уравнений приводим к ступенчатому (в частном случае, когда  , к треугольному) виду с помощью элементарных преобразований.
, к треугольному) виду с помощью элементарных преобразований.
На втором этапе (обратный ход) последовательно определяем значения переменных из полученной ступенчатой системы.
Если ступенчатая система окажется треугольной, то исходная система имеет единственное решение. Из последнего уравнения находим значение  , из предпоследнего -
, из предпоследнего -  , и далее, поднимаясь по системе вверх, найдем значения всех остальных переменных
, и далее, поднимаясь по системе вверх, найдем значения всех остальных переменных  .
.
Если в результате элементарных преобразований появляются уравнения 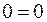 , то их вычеркиваем. Если же появляется уравнение
, то их вычеркиваем. Если же появляется уравнение  , то это свидетельствует о несовместности системы.
, то это свидетельствует о несовместности системы.
Преобразования Гаусса удобнее проводить не с самой системой, а с ее расширенной матрицей, выполняя элементарные преобразования над строками.
Удобно, чтобы коэффициент  был равен
был равен  . Для этого можно переставить уравнения системы либо разделить обе части первого уравнения на
. Для этого можно переставить уравнения системы либо разделить обе части первого уравнения на  .
.
Пример 1. Решить систему уравнений методом Гаусса 
¦ Прямой ход.
1. Выберем «ведущим» третье уравнение и запишем его на первое место.

2. Запишем расширенную матрицу системы и выполним элементарные преобразования над ее строками:
 ~ ~
|  ~ ~
|
первую строку перепишем,
а вторую и третью заменим
суммой с первой, умноженной
соответственно на  и на и на  ; ;
| разделим вторую строку на  . .
|
 ~ ~
|  ~ ~
|
первую и вторую строки перепишем, а третью заменим суммой ее со второй, умноженной на  ; ;
| из этой матрицы запишем систему треугольного вида. |
Обратный ход.

Из третьего уравнения находим значение  , из второго - значение
, из второго - значение  , из первого - значение
, из первого - значение  .
.
Ответ:  . ?
. ?
Пример 2. Решить систему уравнений

¦ Запишем расширенную матрицу системы. Выполняя элементарные преобразования над ее строками, получим:
 ~
~  ~
~
~  ~
~  .
.
Из последней матрицы запишем систему
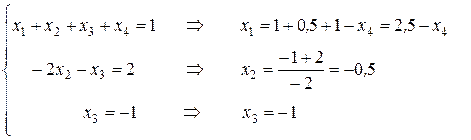
Из третьего уравнения находим значение  , из второго - значение
, из второго - значение  .
.
Так как уравнений в системе осталось меньше, чем переменных, то из первого уравнения выражаем  через
через 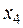 (
(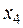 - свободная переменная, т.е.
- свободная переменная, т.е.  - любое число).
- любое число).
Следовательно, система уравнений имеет бесконечно много решений.
Ответ:  , где
, где  - любое число. ?
- любое число. ?




