1. Умножение вектора на число. Произведением вектора 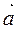 на число
на число  называется вектор
называется вектор  , который имеет длину
, который имеет длину  , коллинеарен вектору
, коллинеарен вектору 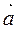 , имеет направление вектора
, имеет направление вектора 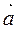 , если
, если  , и противоположное направление, если
, и противоположное направление, если  .
.
Например, если дан вектор 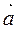 , то векторы
, то векторы  и
и  будут иметь вид:
будут иметь вид:

 2. Сложение векторов. Пусть даны произвольные векторы
2. Сложение векторов. Пусть даны произвольные векторы 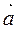 и
и  .Сумму векторов можно построить по правилу треугольника и по правилу параллелограмма.
.Сумму векторов можно построить по правилу треугольника и по правилу параллелограмма.
3. Вычитание векторов  можно заменить сложением вектора
можно заменить сложением вектора 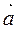 с вектором, противоположным вектору
с вектором, противоположным вектору  .
.

4. Свойства линейных операций.
1) 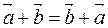
| - переместительное свойство сложения; |
2) 
| - сочетательное свойство сложения; |
3) 
| - сочетательное свойство умножения на число; |
4) 
| - распределительное свойство относительно суммы чисел; |
5) 
| - распределительное свойство относительно суммы векторов. |
Разложение вектора по базису. Координаты вектора
Модуль вектора. Направляющие косинусы

Пусть  - единичные векторы осей координат, т.е.
- единичные векторы осей координат, т.е.  и каждый из них одинаково направлен с координатными осями. Тройка векторов
и каждый из них одинаково направлен с координатными осями. Тройка векторов  называется координатным базисом.
называется координатным базисом.
Теорема. Любой вектор пространства можно разложить по базису  , т.е. представить в виде
, т.е. представить в виде  , где
, где  - некоторые числа (буквы:
- некоторые числа (буквы:  - «мю»,
- «мю», 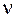 - «ню»).
- «ню»).
Это разложение единственное.
q Доказательство. Приложим вектор 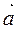 к началу координат, обозначим его конец
к началу координат, обозначим его конец  . Проведем через точку
. Проведем через точку  плоскости, перпендикулярные осям координат. Пусть
плоскости, перпендикулярные осям координат. Пусть  ,
, 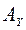 ,
, 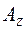 -точки пересечения этих плоскостей с осями координат.
-точки пересечения этих плоскостей с осями координат.
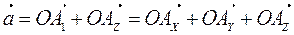
Существует единственная тройка чисел  ,
, 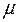 ,
,  таких, что
таких, что 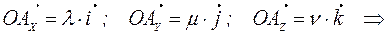
 n.
n.
Формула  называется разложением вектора по координатному базису.
называется разложением вектора по координатному базису.
Числа  ,
, 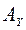 ,
, 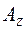 -называются координатами вектора
-называются координатами вектора 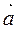 , т.е. координаты вектора есть его проекции на соответствующие координатные оси. В символическом виде записывают
, т.е. координаты вектора есть его проекции на соответствующие координатные оси. В символическом виде записывают  .
.
Например, если  , то его координаты
, то его координаты 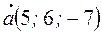 .
.
Зная координаты вектора 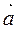 , длину его можно найти по формуле
, длину его можно найти по формуле

Если известны координаты точек  и
и  , то координаты вектора равны:
, то координаты вектора равны:  .
.
Пусть углы вектора 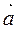 с осями
с осями  ,
, 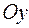 ,
,  соответственно равны
соответственно равны  ,
,  ,
, 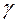 . Числа
. Числа  ,
, 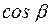 ,
,  называются направляющими косинусами вектора
называются направляющими косинусами вектора 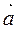 .
.
 ;
;  ;
;  ;
;
 - основное свойство направляющих косинусов вектора.
- основное свойство направляющих косинусов вектора.
Действия над векторами, заданными координатами
Пусть векторы  и
и  заданы своими координатами.
заданы своими координатами.
При сложении (вычитании) векторов их одноименные координаты складываются (вычитаются), т.е. 
При умножении вектора на число  координаты его умножаются на это число, т.е.
координаты его умножаются на это число, т.е.  .
.
Если вектор 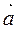 коллинеарен вектору
коллинеарен вектору  , то можно записать
, то можно записать  , где
, где  - некоторое число, т.е.
- некоторое число, т.е.  ,
,  ,
, 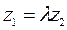 . Отсюда,
. Отсюда,  ,
,  ,
,  или
или  - условие коллинеарности векторов.
- условие коллинеарности векторов.






