Определение. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Определение. Тройка векторов 
называется упорядоченной, если сказано, какой из них считать первым, какой вторым, какой третьим.
Например, в записи 
: 
- первый вектор, 
- второй, 
- третий.
Определение. Упорядоченная тройка трех некомпланарных векторов называется правой, если из конца третьего вектора кратчайший поворот первого ко второму виден совершающимся против
часовой стрелки.
В противном случае тройка называется левой.
Определение. Векторным произведением векторов и называется вектор , удовлетворяющий условиям:
1)  ,  ,
| 2)  ,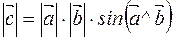
| 3) - правая
тройка векторов.
|
Обозначается: 
или 
.
Если векторы заданы своими координатами 
, 
, то векторное произведение выражается по формуле:
Пример. Даны векторы 
, 
. Найти .
¦ 
Ответ: 
. ?
Свойства векторного произведения
1. 
| 2. 
|
3. 
| 4. 
|
5.  ,
 ,  , 
|
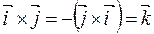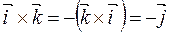Приложения векторного произведения
1. Установление параллельности векторов: .
2. Вычисление площадей параллелограмма и треугольника: 
, 
.
В физике:
3. Определение момента силы относительно точки.
Пусть к точке 
приложена сила 
, точка 
- произвольная точка пространства.
Моментом силы 
относительно точки 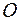является вектор, проходящий через точку 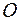, для которого выполняются условия:
 1.  =  ,
| 
|
2.  и  ,
| |
3.  и  - образуют правую тройку.
|
4. Нахождение линейной скорости вращения.
Скорость 
точки 
твердого тела, вращающегося с угловой скоростью 
вокруг неподвижной оси, равна 
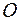( - некоторая точка оси ).
Смешанное произведение векторов
Определение, свойства и вычисление смешанного произведения векторов
Определение. Смешанным произведением векторов называется число, равное 
.
Свойства смешанного произведения векторов:
1. Знаки в смешанном произведении можно расставлять произвольно или вообще опускать, т.е.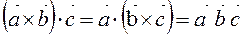 
.
2. Переставлять векторы можно только в круговом порядке:
= 
= 
= 
.
3. Знак смешанного произведения изменится на противоположный, если поменять местами два соседних вектора: 
.
4. Есл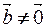и 
, 
, 
и 
векторы компланарны.
Вычисление смешанного произведения.
, , 
.
Приложения смешанного произведения
1. Установление компланарности векторов 
.
2. Определение взаимной ориентации в пространстве:
если 
- правая тройка,
если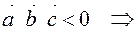 
- левая тройка.
3. Вычисление объемов параллелепипеда и пирамиды, построенных на векторах : 
, 
.
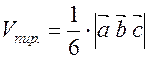Пример 1. Показать, что векторы 
, 
, 
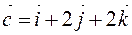компланарны.
¦ 
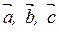- компланарны. ?
Пример 2. Найтиобъем треугольной пирамиды с вершинами 
, 
, 
, 
.
¦ 
, 
, 
.
. ?
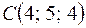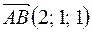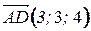Глава III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Системы координат на плоскости
