Пусть прямые  и
и  заданы общими уравнениями и уравнениями с угловыми коэффициентами.
заданы общими уравнениями и уравнениями с угловыми коэффициентами.

| 
|

| 
|
 1. 1.  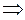  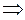

|
       
|
2.  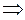  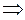 

|
  
|
3.  


|

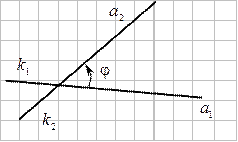 ( ( - угловой коэффициент прямой, которую поворачиваем) - угловой коэффициент прямой, которую поворачиваем)
|
Расстояние от точки до прямой находим по формуле 

Пример. Найти расстояние от точки  до прямой
до прямой 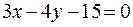 .
.
¦ Расстояние  от точки до прямой равно:
от точки до прямой равно:
 ?
?
Линии второго порядка на плоскости
Эллипс
Определение. Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек  и
и  , называемых фокусами, есть величина постоянная
, называемых фокусами, есть величина постоянная 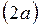 , большая, чем расстояние между фокусами
, большая, чем расстояние между фокусами 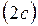 .
.
Каноническое уравнение эллипса имеет вид:
 , где
, где  .
.
 Расположим систему координат следующим образом: за ось
Расположим систему координат следующим образом: за ось  примем прямую, проходящую через фокусы
примем прямую, проходящую через фокусы  и
и  , за ось
, за ось  примем перпендикуляр к оси абсцисс, проходящий через середину отрезка
примем перпендикуляр к оси абсцисс, проходящий через середину отрезка 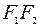 .
.
 ,
,  ,
,  и
и  - точки пересечения эллипса с осями симметрии
- точки пересечения эллипса с осями симметрии
(координатными осями) называются вершинами эллипса.
Отрезки  и
и  называются осями эллипса, причем
называются осями эллипса, причем  - большая ось, а
- большая ось, а  - малая ось, так как
- малая ось, так как  .
.
Параметры 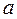 и
и  , входящие в каноническое уравнение, называются полуосями эллипса, а
, входящие в каноническое уравнение, называются полуосями эллипса, а  называется фокусным расстоянием эллипса.
называется фокусным расстоянием эллипса.
Эксцентриситетом эллипса называется отношение фокусного расстояния к большей полуоси  . Очевидно, что
. Очевидно, что  .
.
Прямые  называются директрисами эллипса
называются директрисами эллипса  .
.
Пусть точка  - произвольная точка эллипса.
- произвольная точка эллипса.
Длины отрезков  и
и  называются фокальными радиусами
называются фокальными радиусами  .
.
 и
и 

Если фокусы эллипса лежат на оси  , то большей осью будет отрезок
, то большей осью будет отрезок  ,
,
а малой осью отрезок  .
.
Тогда  , а директрисами
, а директрисами  являются прямые
являются прямые  .
.
Если 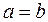 , то эллипс превращается в окружность, определяемую уравнением
, то эллипс превращается в окружность, определяемую уравнением
 .
.
Уравнение  определяет вырожденный эллипс, т.е. это уравнение определяет на плоскости
определяет вырожденный эллипс, т.е. это уравнение определяет на плоскости  только одну точку
только одну точку  .
.
Уравнение  определяет мнимый эллипс, т.е. это уравнение не определяет на плоскости
определяет мнимый эллипс, т.е. это уравнение не определяет на плоскости  никакого геометрического образа.
никакого геометрического образа.
Если центр эллипса находится в точке  и оси параллельны осям координат, то его уравнение имеет вид:
и оси параллельны осям координат, то его уравнение имеет вид:

Гипербола
Определение. Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек  и
и  , называемых фокусами гиперболы, есть величина постоянная
, называемых фокусами гиперболы, есть величина постоянная 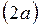 , меньшая, чем расстояние между фокусами
, меньшая, чем расстояние между фокусами 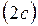 .
.
Каноническое уравнение гиперболы имеет вид  , где
, где 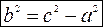 .
.

Расположим систему координат следующим образом: за ось  примем прямую, проходящую через фокусы
примем прямую, проходящую через фокусы  и
и  , за ось
, за ось  примем перпендикуляр к оси абсцисс, проходящий через середину отрезка
примем перпендикуляр к оси абсцисс, проходящий через середину отрезка 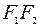 .
.
Гипербола имеет две оси симметрии (оси координат), с одной из которых она пересекается в точках  ,
,  , называемых вершинами гиперболы.
, называемых вершинами гиперболы.
Отрезок  - действительная ось,
- действительная ось,  - мнимая ось.
- мнимая ось.
Параметры 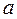 и
и  , входящие в каноническое уравнение, называются полуосями гиперболы, а
, входящие в каноническое уравнение, называются полуосями гиперболы, а  называется фокусным расстоянием гиперболы.
называется фокусным расстоянием гиперболы.
Прямоугольник со сторонами  и
и  называется основным прямоугольником гиперболы.
называется основным прямоугольником гиперболы.
Диагонали этого прямоугольника называются асимптотами гиперболы.
Уравнения асимптот имеют вид: 
Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине действительной полуоси  . Очевидно, что
. Очевидно, что  .
.
Прямые  называются директрисами гиперболы
называются директрисами гиперболы  .
.
Пусть точка  - произвольная точка гиперболы.
- произвольная точка гиперболы.
Длины отрезков  и
и  называются фокальными радиусами
называются фокальными радиусами  .
.
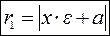 и
и 
Если гипербола расположена так, что ее фокусы лежат на оси  , то действительной осью будет отрезок
, то действительной осью будет отрезок  , а мнимой осью - отрезок
, а мнимой осью - отрезок  и уравнение ее имеет вид
и уравнение ее имеет вид 
 Тогда
Тогда  и директрисами
и директрисами  являются прямые
являются прямые  , а асимптоты будут те же, что и у гиперболы (1).
, а асимптоты будут те же, что и у гиперболы (1).
Гиперболы (1) и (2) н азываются сопряженными.
Если 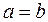 , то гипербола называется равносторонней.
, то гипербола называется равносторонней.
Простейшие уравнения равносторонней гиперболы имеют вид:
 ,
,  .
.
Если центр гиперболы находится в точке  и оси параллельны осям координат, то уравнение ее имеет вид:
и оси параллельны осям координат, то уравнение ее имеет вид:
 или
или  .
.
Парабола
Определение. Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки  , называемой фокусом, и данной прямой
, называемой фокусом, и данной прямой  , называемой директрисой.
, называемой директрисой.
Величина  , равная расстоянию от фокуса до директрисы, называется параметром параболы.
, равная расстоянию от фокуса до директрисы, называется параметром параболы.
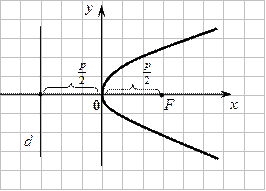
Расположим систему координат следующим образом: за одну из координатных осей примем ось параболы, а за другую – прямую, перпендикулярную оси и проведенную посередине между фокусом и директрисой.
Тогда уравнения параболы будут иметь вид:
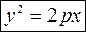
| 

|


|


|
Пусть вершина параболы находится в точке  , тогда ее уравнения имеют вид:
, тогда ее уравнения имеют вид:
если ось параболы параллельна оси  , то
, то  ;
;
если ось параболы параллельна оси  , то
, то  .
.
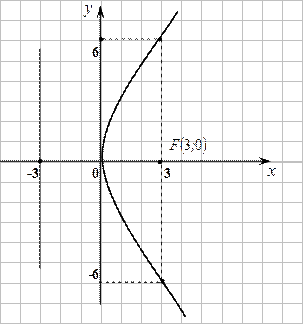 Пример. Построить параболу
Пример. Построить параболу  . Записать координаты фокуса и уравнения директрисы.
. Записать координаты фокуса и уравнения директрисы.
¦ Из канонического уравнения параболы определим:
1) 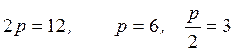 .
.
2) Ось параболы -  , вершина - точка
, вершина - точка  , фокус -
, фокус -  , директриса - прямая
, директриса - прямая  .
.
3) Из определения параболы следует, что параболе принадлежат точки, которые лежат на прямой, параллельной директрисе, на расстоянии  от фокуса. ?
от фокуса. ?






