Рассмотрим частные случаи расположения плоскости  , определяемой общим уравнением:
, определяемой общим уравнением: 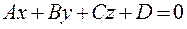 .
.
1. Если  ,то
,то 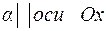 .
.
 , то
, то 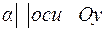 .
.
Если 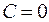 , то
, то 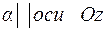 .
.
Если  , то
, то  проходит через начало координат.
проходит через начало координат.
2. Если  , то
, то  .
.
Если  , то
, то  .
.
Если 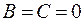 , то
, то  .
.
3. Если  , то
, то  проходит через ось
проходит через ось  .
.
Если  , то
, то  проходит через ось
проходит через ось  .
.
Если  , то
, то  проходит через ось
проходит через ось  .
.
4. Если  - это уравнение плоскости
- это уравнение плоскости 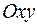 .
.
Если  - это уравнение плоскости
- это уравнение плоскости  .
.
Если  - это уравнение плоскости
- это уравнение плоскости 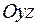 .
.
5. Если  , то уравнение плоскости
, то уравнение плоскости  можно привести к виду:
можно привести к виду: 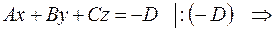
 или
или  . Обозначив
. Обозначив  ,
,
получим 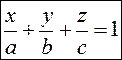 (3) – уравнение плоскости в отрезках на осях,
(3) – уравнение плоскости в отрезках на осях,
где  ,
, 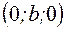 ,
,  - точки пересечения с осями координат.
- точки пересечения с осями координат.
Примеры. Построить плоскости, заданные общими уравнениями:

1. 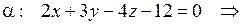
 .
.
2. 
 . .

| 3. 
  . .
|
4. 
 . .

| 5. 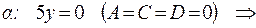
 . .
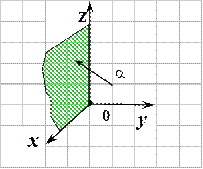
|
Уравнение плоскости, проходящей через три точки

Пусть даны точки 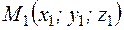 ,
,  ,
, 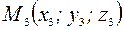 принадлежащие плоскости
принадлежащие плоскости  .
.
Точка  - произвольная точка плоскости
- произвольная точка плоскости  .
.
Построим векторы: 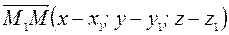 ,
,
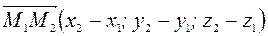 ,
,
 .
.
Так как точки лежат в одной плоскости, то векторы компланарны. Следовательно, их смешанное произведение равно нулю.
 (4) (4)
| - уравнение плоскости, проходящей через три точки. |
Пример. Составить уравнение плоскости, проходящей через точки  ,
,  ,
,  .
.
¦ Используем уравнение (4):


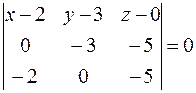


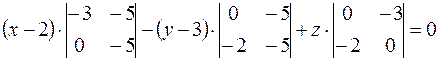




 . ?
. ?
Нормальное уравнение плоскости
 1. Пусть в системе координат
1. Пусть в системе координат 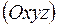 задана плоскость
задана плоскость  .
.
Проведем через начало координат прямую, перпендикулярную плоскости  .
.
Будем называть ее нормалью.
Точку пересечения нормали с плоскостью обозначим 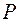 . Построим вектор
. Построим вектор 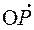 , длину которого обозначим
, длину которого обозначим  .
.
Введем единичный вектор  , направление которого совпадает с направлением вектора
, направление которого совпадает с направлением вектора 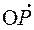 .
.
Пусть 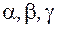 - углы, которые составляет вектор
- углы, которые составляет вектор  с осями координат. Так как
с осями координат. Так как  , то
, то 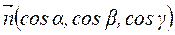 .
.
2. Выведем уравнение плоскости  , считая известными числа
, считая известными числа 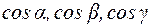 и
и  .
.
Пусть  - произвольная точка. Она лежит в плоскости
- произвольная точка. Она лежит в плоскости  тогда и только тогда, когда проекция вектора
тогда и только тогда, когда проекция вектора 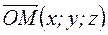 на нормаль равна
на нормаль равна  . Таким образом,
. Таким образом,
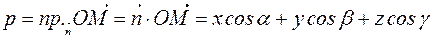

 (5) (5)
| - нормальное уравнение плоскости |
3. Покажем, как привести общее уравнение плоскости к нормальному виду.

| - общее уравнение. (1) |
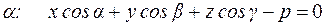
| - нормальное уравнение. (2) |
Так как 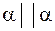 то, умножая, коэффициенты уравнения (1) на некоторый множитель
то, умножая, коэффициенты уравнения (1) на некоторый множитель  , получим уравнение
, получим уравнение  , совпадающее с уравнением (2), т. е
, совпадающее с уравнением (2), т. е
 .
.
Возведем первые три из равенств в квадрат и почленно сложим:
 
| - нормирующий множитель. |
Знак его противоположен знаку  в общем уравнении, т. к.
в общем уравнении, т. к.  .
.
Пример. Привести уравнение плоскости 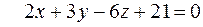 к нормальному виду.
к нормальному виду.
¦  ,
, 
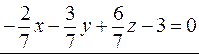 - это и есть нормальное уравнение плоскости
- это и есть нормальное уравнение плоскости  .?
.?
Пучок плоскостей
 Пусть плоскости
Пусть плоскости  и
и  пересекаются по прямой a.
пересекаются по прямой a.

Определение. Плоскости, проходящие через линию пересечения двух плоскостей, образуют пучок плоскостей.
Уравнение пучка плоскостей:  .
.
Чтобы написать уравнение какой-либо плоскости пучка, достаточно знать точку, через которую она проходит.
Пример. Написать уравнение плоскости  , проходящей через линию пересечения плоскостей
, проходящей через линию пересечения плоскостей  и
и  , и через точку
, и через точку  .
.
¦ Запишем уравнение пучка плоскостей:
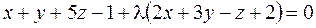 .
.
Значение 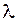 определяем из условия, что плоскость проходит через точку
определяем из условия, что плоскость проходит через точку  :
: 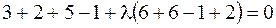 , или
, или  .
.
Следовательно, искомое уравнение имеет вид:
 или
или  . ?
. ?






