Пусть прямая 
задана общим уравнением 
.
Если 
, то прямая проходит через начало координат;
, то 
;
, то 
;
Если 
, то 
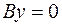
- это ось 
;
, то 
- это ось 
;
Если 
.
можно преобразовать к виду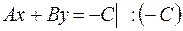 
,
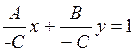
, обозначим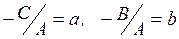 
Получим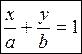 
| (3) – уравнение прямой в отрезках на осях, |
где 
и 
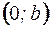- точки пересечения с осями координат.
Уравнение (3) используется при построении прямой в системе координат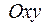 
.
Пример 1. Построить прямую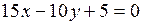 
.
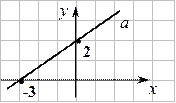¦ Приведем уравнение 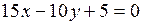к уравнению в отрезках на осях
. ?
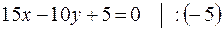
Пример 2. Построить прямую 
.
¦ Приведем уравнение к уравнению в отрезках на осях
, 
, 
. ?
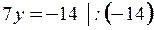12.3. Уравнение прямой, проходящей через данную точку:
А) параллельной данной прямой;
Б) перпендикулярной данной прямой.
а) Пусть прямая задана общим уравнением 
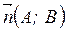, а прямая 
параллельна прямой
и проходит через точку 
.
Составим уравнение прямой .
Произвольная точка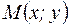 
будет лежать на прямой , если 
, 
.
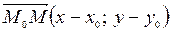Из условия перпендикулярности векторов получим уравнение прямой .
| (4) – уравнение прямой, проходящей через данную точку и параллельной данной прямой. |
б) Пусть прямая задана общим уравнением 
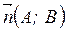, а прямая перпендикулярна прямой и проходит через точку . Составим уравнение прямой . Произвольная точка 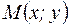будет принадлежать прямой , если 
, .
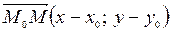Из условия параллельности векторов получаем уравнение прямой .
| (5) – уравнение прямой, проходящей через данную точку и перпендикулярной данной прямой |
Уравнение прямой, проходящей через две точки.
Каноническое уравнение прямой.
Параметрические уравнения прямой.
1. Пусть точки 
и 
лежат на прямой . Произвольная точка 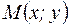будет лежать на прямой тогда и только тогда, когда 
,
, 
.
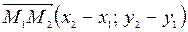Из условия параллельности векторов получим уравнение.
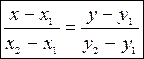
| (6) – уравнение прямой, проходящей через две точки |
2. Пусть вуравнении (6)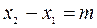 
, 
, 
.
Тогда получим
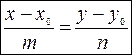
| (7) – каноническое уравнение прямой |
3. Пусть в каноническом уравнении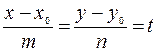 
,
где 
- параметр, 
.
Тогда 
| 
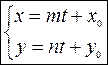
| (8) – параметрические уравнения прямой |
Уравнение прямой с угловым коэффициентом
Положение прямой на плоскости 
определяется ординатой точки 
(точки пересечения прямой с осью 
) и углом 
(угол между прямой и осью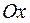 
).
Возьмем на прямой произвольную точку 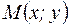. Через точку 
проведем отрезок 
, параллельный оси .
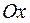Тогда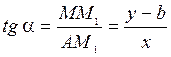 
.
Обозначим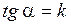 
- угловой коэффициент прямой.
Получим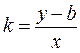 
| или 
| (9) – уравнение прямой с угловым коэффициентом |
Если прямая проходит через точку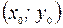 
и известен угловой коэффициент 
, то
| (10) – уравнение прямой, проходящей через данную точку в данном направлении |
Взаимное расположение прямых на плоскости.