СОДЕРЖАНИЕ
Глава I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
§ 1. Матрицы. Виды матриц 3
§ 2. Действия над матрицами.................................................................................................... 5
2.1. Умножение на число. Сложение и вычитание.......................................................... 5
2.2. Умножение матриц....................................................................................................... 6
2.3. Возведение в степень. Транспонирование матрицы............................................... 7
§ 3. Определители....................................................................................................................... 7
3.1. Основные понятия........................................................................................................ 7
3.2. Свойства определителей.............................................................................................. 8
§ 4. Обратная матрица................................................................................................................ 10
4.1. Основные понятия......................................................................................................... 10
4.2. Вычисление обратной матрицы методом присоединенной матрицы..................... 10
4.3. Вычисление обратной матрицы методом элементарных преобразований............. 11
§ 5. Системы m линейных уравнений с n переменными..................................................... 12
5.1. Основные понятия........................................................................................................ 12
5.2. Системы n линейных уравнений с n переменными.
Формулы Крамера. Метод обратной матрицы........................................................... 14
5.3. Метод Гаусса................................................................................................................. 15
Глава II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
§ 6. Прямоугольная система координат в пространстве........................................................ 17
§ 7. Векторы................................................................................................................................ 18
7.1. Основные понятия......................................................................................................... 18
7.2. Линейные операции над векторами............................................................................ 18
7.3. Разложение вектора по базису. Координаты вектора.
Модуль вектора. Направляющие косинусы................................................................. 20
7.4. Действия над векторами, заданными координатами................................................. 21
7.5. Деление отрезка в данном отношении........................................................................ 21
§ 8. Скалярное произведение векторов.................................................................................... 22
8.1. Определение скалярного произведения..................................................................... 22
8.2. Свойства скалярного произведения........................................................................... 23
8.3. Вычисление скалярного произведения векторов через координаты...................... 23
8.4. Приложения скалярного произведения векторов..................................................... 24
§ 9. Векторное произведение векторов.................................................................................... 25
9.1. Определение и вычисление векторного произведения векторов........................... 25
9.2. Свойства векторного произведения........................................................................... 26
9.3. Приложения векторного произведения..................................................................... 27
§ 10. Смешанное произведение векторов................................................................................ 27
10.1. Определение, свойства и вычисление смешанного
произведения векторов.................................................................................................. 27
10.2. Приложения смешанного произведения.................................................................. 28
Глава III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
§ 11. Системы координат на плоскости................................................................................... 29
11.1. Прямоугольная и полярная системы координат..................................................... 29
11.2. Связь между прямоугольными и полярными координатами................................ 30
11.3. Преобразование прямоугольных координат........................................................... 31
§ 12. Прямая на плоскости......................................................................................................... 33
12.1. Общее уравнение прямой на плоскости.................................................................. 33
12.2. Частные случаи расположения прямой на плоскости.
Уравнение в отрезках на осях........................................................................................ 34
12.3. Уравнение прямой, проходящей через данную точку:
а) параллельной данной прямой;
б) перпендикулярной данной прямой................................................................. 35
12.4. Уравнение прямой, проходящей через две точки.
Каноническое уравнение прямой.
Параметрические уравнения прямой...................................................................... 35
12.5. Уравнение прямой с угловым коэффициентом....................................................... 36
12.6. Взаимное расположение прямых на плоскости.
Расстояние от точки до прямой..................................................................................... 37
§ 13. Линии второго порядка на плоскости............................................................................. 38
13.1. Эллипс......................................................................................................................... 38
13.2. Гипербола..................................................................................................................... 40
13.3. Парабола....................................................................................................................... 41
13.4. Общее уравнение линии второго порядка................................................................ 43
Глава IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
§ 14. Плоскость........................................................................................................................... 44
14.1. Общее уравнение плоскости...................................................................................... 44
14.2. Расположение плоскости в пространстве.
Уравнение плоскости в отрезках на осях..................................................................... 45
14.3. Уравнение плоскости, проходящей через три точки............................................... 47
14.4. Нормальное уравнение плоскости............................................................................. 47
14.5. Пучок плоскостей........................................................................................................ 49
14.6. Взаимное расположение плоскостей.
Расстояние от точки до плоскости................................................................................ 50
§ 15. Прямая в пространстве...................................................................................................... 51
15.1. Общие, канонические и параметрические уравнения прямой............................... 51
15.2. Уравнения прямой, проходящей через две точки.................................................... 52
15.3. Взаимное расположение прямых в пространстве.
Условие принадлежности двух прямых одной плоскости......................................... 53
§ 16. Прямая и плоскость в пространстве.
Условие принадлежности прямой плоскости.............................................................. 54
§ 17. Поверхности второго порядка......................................................................................... 56
17.1. Эллипсоид.................................................................................................................... 56
17.2. Однополостный гиперболоид.................................................................................... 57
17.3. Двуполостный гиперболоид...................................................................................... 58
17.4. Эллиптический параболоид....................................................................................... 60
17.5. Гиперболический параболоид.................................................................................... 61
17.6. Конус второго порядка................................................................................................ 62
17.7. Цилиндрические поверхности................................................................................... 63
Литература................................................................................................................................... 66
Глава I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Матрицы. Виды матриц
Определение. Матрицей размера  называется прямоугольная таблица чисел, содержащая
называется прямоугольная таблица чисел, содержащая  строк и
строк и  столбцов.
столбцов.
Числа, составляющие матрицу, называются ее элементами.
Матрицы обозначаются заглавными буквами латинского алфавита А, В, С, а для обозначения элементов матрицы используются, соответственно, строчные буквы с двойными индексами:  , где i – номер строки, j – номер столбца.
, где i – номер строки, j – номер столбца.
| Записывают матрицу так | 
|
или в сокращенном виде:  , где
, где  ,
, 
(i принимает значения от 1 до  ; j принимает значения от 1 до
; j принимает значения от 1 до 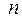 ).
).
Например,  .
.
Наряду с круглыми скобками используются и другие обозначения:  .
.
Определение. Матрицы одного размера называются равными, если их элементы совпадают, т.е.  , для любых
, для любых  ,
,  .
.
Виды матриц.
1. Матрица, состоящая из одной строки, называется
матрицей (вектором) - строкой:  .
.
| 2. Матрица, состоящая из одного столбца, называется матрицей (вектором)- столбцом: |  . .
|
3. Матрица, содержащая одну строку и один столбец, отождествляется с числом.  - есть число
- есть число  .
.  - есть число
- есть число  .
.
4. Матрица называется квадратной 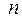 - го порядка, если число ее строк равно числу столбцов и равно
- го порядка, если число ее строк равно числу столбцов и равно 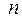 .
.
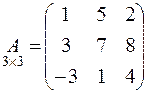 - квадратная матрица 3-го порядка.
- квадратная матрица 3-го порядка.
Определение. Элементы матрицы  , у которыхномер строки равен номеру столбца
, у которыхномер строки равен номеру столбца  , называются диагональными элементами и образуют главную диагональ матрицы.
, называются диагональными элементами и образуют главную диагональ матрицы.
5. Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
Например,  - диагональная матрица 3-го порядка.
- диагональная матрица 3-го порядка.
6. Диагональная матрица 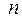 -го порядка, все диагональные элементы которой равны 1, называется единичной матрицей
-го порядка, все диагональные элементы которой равны 1, называется единичной матрицей 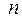 - го порядка.
- го порядка.
Она обозначается буквой Е.
Например,  - единичная матрица 3-го порядка.
- единичная матрица 3-го порядка.
7. Матрица любого порядка, все элементы которой равны нулю, называется нулевой матрицей. Она обозначается буквой О.
Например,  - нулевая матрица.
- нулевая матрица.
Матрицы Е и О играют ту же роль, что и числа 1 и 0 в арифметике.
Действия над матрицами
Умножение на число. Сложение и вычитание
1. Умножение матрицы на число возможно для матриц любого размера.
Определение. Произведением матрицы  на число
на число  называется матрица
называется матрица  , каждый элемент которой
, каждый элемент которой  для
для  ,
,  .
.
Например,  .
.
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
В частном случае число 0, умноженное на  , есть нулевая матрица, т.е.
, есть нулевая матрица, т.е.  .
.
2. Сложение матриц возможно только для матриц одинакового размера.
Определение. Суммой матриц  и
и  называется матрица
называется матрица 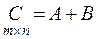 , каждый элемент которой
, каждый элемент которой  для
для  ,
,  . (т.е. матрицы складываются поэлементно).
. (т.е. матрицы складываются поэлементно).
В частном случае  .
.
Например,
 .
.
3. Вычитание матриц можно выполнить с помощью двух предыдущих операций, т.е.
 .
.
Умножение матриц
Умножение матрицы  на матрицу
на матрицу  возможно, когда число столбцов первой матрицы (
возможно, когда число столбцов первой матрицы ( ) равно числу строк второй матрицы (
) равно числу строк второй матрицы ( ).
).
 В результате получается матрица, число строк которой равно числу строк матрицы
В результате получается матрица, число строк которой равно числу строк матрицы  ; а число столбцов равно числу столбцов матрицы
; а число столбцов равно числу столбцов матрицы  .
.
Схема: 
Определение. Произведением матриц  и
и  называется матрица
называется матрица  , каждый элемент которой
, каждый элемент которой  равен сумме произведений элементов
равен сумме произведений элементов  - й строки первой матрицы (
- й строки первой матрицы ( ) на соответствующие элементы
) на соответствующие элементы  - го столбца второй матрицы (
- го столбца второй матрицы ( ).
).
Схема вычисления:











Например,  .
.
 .
.
В частном случае  .
.
Многие свойства операций над числами выполняются и для операций над матрицами:
1)  + +  = =  + + 
| 6) 
|
2)  +( +( + +  )=( )=( + +  )+ )+ 
| 7) 
|
3) 
| 8) 
|
4) 
| 9) 
|
5) 
|
Однако некоторые свойства произведения чисел не выполняются для произведения матриц:
- произведение  не всегда равно
не всегда равно  ;
;
(если  , то матрицы называются перестановочными).
, то матрицы называются перестановочными).
- произведение двух ненулевых матриц может равняться нулевой матрице: 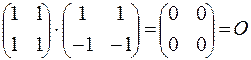 .
.






