xD =, yD =.
Отсюда находим
xB = 2 xD – xC = –1, yB = 2 yD – yC =1, B (–1, 1).
Аналогично, используя тот факт, что О – середина АВ, находим координаты точки А (-2,-7). Возможен другой путь решения этой задачи: достроить Δ ABC до параллелограмма.
Общие формулы деления отрезка в данном отношении выглядят так:
xС =, yD =,
если точка С делит отрезок АВ в отношении l1:l2, т.е. ½ AC ½:½ BC ½=l1:l2.
Известно, что точка пересечения медиан делит медиану в отношении 2:1, считая от вершины. В нашем случае Р делит СО в отношении 2:1. Поэтому
xP = = = –,
yP = = = –.
Ответ: А (–2,–7), B (–1, 1), P.
3. Даны координаты вершин A (– 4,–2), B (9, 7), C (2,– 4) треугольника ABC. Составить общее уравнение биссектрисы AD и найти координаты точки D.
Решение. Из курса элементарной математики известно, что =. Вычисляем
(13, 9), (6,–2);
½½= = 5, ½½= = 2.
Значит BD: DC = 5 : 2. Далее, применяя формулы деления отрезка в заданном отношении (см. задачу 16) находим
xD = = = 4,
yD = = = –, D (4,– ).
Составляем уравнение прямой, проходящей через точки A и D. Для неё вектор является направляющим. Но, в качестве направляющего мы можем взять любой вектор, коллинеарный. Например, удобно будет взять =, (7, 1). Тогда уравнение
AD: = y + 2 Û x – 7 y – 10 = 0.
Ответ: D (4,– ), AD: x – 7 y – 10 = 0.
4. Даны уравнения двух медиан x – y – 3 = 0, 5 x + 4 y – 9 = 0 треугольника ABC и координаты вершины A (– 1, 2). Составьте уравнение третьей медианы.
Решение. Сначала мы убедимся, что точка A не принадлежит данным медианам. Медианы треугольника пересекаются в одной точке M. Поэтому они входят в пучок прямых, проходящих через M. Составим уравнение этого пучка:
l( x – y – 3) + m(5 x + 4 y – 9) = 0.
Коэффициенты l и m определяются с точностью до пропорциональности; поэтому можем считать, что m = 1 (если m = 0 то уравнение пучка задает только первую медиану, а искомая прямая не совпадает с ней). Получаем уравнение пучка:
(l + 5) x + (–l + 4) y – 3l – 9 = 0.
Нам из этого пучка надо выбрать прямую, проходящую через точку A (– 1, 2). Подставим её координаты в уравнение пучка:
– (l + 5) + 2(–l + 4) – 3l – 9 = 0,
– 6l – 6 = 0, l = –1.
Найденное значение l подставляем в уравнение пучка и получаем искомое уравнение медианы:
4 x + 5 y – 6 = 0.
Ответ: 4 x + 5 y – 6 = 0.
5. Даны координаты вершин треугольной пирамиды SABC: A (–3, 7, 1), B (–1, 9, 2), C (–3, 6, 6) S (6,–5,–2). Составить уравнение плоскости основания ABC и уравнение высоты SD. Найти координаты точки D и точки S ¢, симметричной S относительно плоскости основания.
Решение. Найдем координаты двух векторов параллельных плоскости основания p = ABC:
= (2, 1, 1), = (0,–1, 5).
Уравнение плоскости, проходящей через данную точку A (x o, y o, z o) параллельно двум неколлинеарным векторам (a 1, a 2, a 3), (b 1, b 2, b 3) имеет вид
x – x o y – y o z – z o
a 1 a 2 a 3 = 0.
b 1 b 2 b 3
Подставляем в это уравнение наши данные:
x + 3 y – 7 z – 1
2 2 1 = 0.
0 –1 5
Раскрываем определитель:
Из уравнения плоскости находим, что вектор (11,–10,–2) является вектором нормали к плоскости. Этот же вектор будет направляющим для прямой h = SD. Параметрическое уравнение прямой, проходящей через данную точку A (x o, y o, z o) с направляющим вектором (a 1, a 2, a 3) имеет вид
x = x o + a 1 t ,
y = y o + a 2 t ,
z = z o + a 3 t .
В нашем случае получаем уравнение:
x = 6 + 11 t ,
h: y = –5 – 10 t , (*)
z = –2 – 2 t .
Найдем основание перпендикуляра. Это точка пересечения прямой 
с плоскостью p. Для этого мы должны решить совместно уравнения и p. Подставляем 
из уравнения l в уравнение π:
11(6 + 11 t) – 10(–5 – 10 t) – 2(–2 – 2 t) + 105 = 0,
66 + 121 t + 50 + 100 t + 4 + 4 t + 105 = 0,
225 y = –225, t = –1.
Найденное t подставляем в уравнение l и находим координаты D (–5, 5, 0).
Вспомним физический смысл параметрического уравнения прямой: оно задает прямолинейное и равномерное движение. В нашем случае, начальная точка – это S, вектор скорости – это. Отрезок SS ¢вдвое длиннее отрезка SD и на его прохождение понадобится вдвое больше времени. Если за время tD = –1 мы прошли путь от S до D, то путь от S до S ¢ мы пройдем за время t ¢= 2 tD = –2. Подставляя это значение в (*), находим S ¢(–16, 15; 2).
Ответ: ABC: 11 x – 10 y – 2 z +105 = 0, D (–5, 5, 0), S ¢(–16, 15; 2),
x = 6 + 11 t ,
SD: y = –5 – 10 t ,
z = –2 – 2 t .
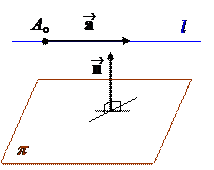
6. Даны уравнения прямой l плоскости p :
Убедиться, что l и p пересекаются и составить уравнение проекции l ¢ прямой l на плоскость. Найти угол между l и p.
Решение. Из уравнения прямой находим ее направляющий вектор: (1,–1, 2) и точку на этой прямой: A (6, 0, 2), а из уравненияплоскости – векторнормали к плоскости:
(5,–2, 4). Очевидно, что если l ½½ p или 
, то ^ т.е. · = 0. Проверим:
· = 5·1 – 2·(–1) + 4·2 = 15 ¹ 0.
Значит, l пересекает π. Угол между l и pнаходим по формуле:
sin a =;
|| = =, || = = = 3.
Отсюда
sin a = =.
Пусть A o – проекция точки A на плоскость, а B = l I π. Тогда l ¢= A o B – это проекция прямой . Найдем сначала координаты точки B. Для этого перепишем уравнение прямой l в параметрическом виде:
x = 6 + t,
l: y = – t,
z = 2 + 2 t,
и решим его совместно с уравнением плоскости π. Подставляем из уравнения l в уравнение π:
5(6 + t ) – 2(– t ) + 4(2 + 2 t ) + 7 = 0,
30 + 5 t + 2 t + 8 + 8 t + 7 = 0,
15 t = – 45, t = – 3.
Подставляя это t в уравнение l находим координаты B (3, 3, 4). Составим уравнение перпендикуляра h = AA o. Для прямой h вектор служит направляющим. Поэтому h задается уравнением
x = 6 + 5 t,
h: y = –2 t,
z = 2 + 4 t,
Решаем его совместно с уравнением плоскости π, чтобы найти координаты точки A o:
5(6 + 5 t ) – 2(–2 t ) + 4(2 + 4 t ) + 7 = 0,
30 + 25 t + 4 t + 8 + 16 t + 7 = 0,
45 t = – 45, t = – 1.
Подставляем это t в уравнение h и находим A o(1, 2,–2). Находим направляющий вектор прямой l': A o B (2, 1,–2) и получаем ее уравнение:
.
7. Прямая l в пространстве задана системой уравнений
2 x +2 y – z – 1=0,
4 x – 8 y + z – 5= 0,
и даны координаты точки A (–5,6,1). Найти координаты точки В, симметричной А относительно прямой l.
Решение. Пусть P – основание перпендикуляра, опущенного из точки A на прямую l. Сначала мы найдем координаты точки P. Для этого мы составим уравнение плоскости p, проходящей через точку A перпендикулярно плоскостям p1 и p2. Находим векторы нормали к этим плоскостям: (2, 2,–1), (4,–8, 1). Для плоскости p они будут направляющими. Поэтому уравнение этой плоскости:
x + 5 y – 6 z – 1
2 2 –1 = 0.
4 –8 1
– 6( x + 5) – 6( y – 6) –24( z – 1) = 0 .
Прежде чем раскрывать скобки обязательно
сначала делим все уравнение на – 6:
x + 5 + y – 6 + 4( z – 1) = 0,
x+ y+ 4 z – 5 = 0.
Теперь P – точка пересечения плоскостей p, p1 и p2 . Для того, чтобы найти ее координаты мы должны решить систему, составленную из уравнений этих плоскостей:
x + y + 4 z – 5 = 0,
4 x – 8 y + z – 5 = 0,
2 x + 2 y – z – 1 = 0.
Решая ее по методу Гаусса, находим P (1,0,1). Далее, используя тот факт, что P – середина AB мы находим координаты точки B (7,–6,1).
Точку P можно найти другим способом, как ближайшую к A точку прямой l . Для этого необходимо составить параметрическое уравнение этой прямой. Как это делается, см. задачу 10. Дальнейшие действия см. в задаче 8.
8. В D ABC с вершинами A (9, 5, 1), B (–3, 8, 4), C (9,–13,–8) проведена высота AD. Найти координаты точки D, составить уравнение прямой AD, вычислить h =½ AD ½ и проверить h, вычислив SD ABC с помощью векторного произведения.
Решение. Очевидно, что точку D можно найти так: D = π I BC, где π – это плоскость, которая проходит через точку A перпендикулярно стороне BC. Для этой плоскости служит вектором нормали. Находим (12,–21,–12). Координаты этого вектора нацело делятся на 3. Поэтому в качестве вектора нормали к p можем взять = , (4,–7,– 4). Уравнение плоскости π, проходящей через точку A o(x o, y o, z o) перпендикулярно вектору (a, b, c), имеет вид:
a (x – x o) + b (y – y o) + c (z – z o) = 0.
В нашем случае:
4(x – 9) - 7(y – 5) - 4(z – 1) = 0,
4 x - 7 y - 4 z + 3 = 0,
Составим уравнение прямой BC. Для нее вектор будет направляющим:
x = –3 + 4 t,
BC: y = 8 – 7 t, (*)
z = 4 – 4 t,
Поскольку D = π I BC, для нахождения координат точки D нужно решить совместно уравнения π и BC. Подставляем из уравнения BC в уравнение π:
4(–3 + 4 t ) – 7(8 – 7 t ) – 4(4 – 4 t ) + 3 = 0,
–12 + 16 t – 56 + 49 t – 16 + 16 t + 3 = 0,
81 t = 81, t = 1.
Подставляем это t в уравнение прямой BC и находим D (1, 1, 0). Далее, зная координаты точек A и D, составляем уравнение прямой AD вычисляем 
по формуле расстояния между точками:
h = = 9.
Далее, SΔ ABC = |´ |; сначала находим сам вектор ´, а потом его модуль.
i j k i j k
´ = –12 3 3 = –27· – 4 1 1 = –27(– i + 4 j – 8 k) .
0 –18 –9 0 2 1
(В процессе вычисления мы воспользовались свойством определителя: общий множитель элементов одной строки можно выносить за знак определителя).
SΔ ABC = · 27 =.
С другой стороны SΔ ABC = | |· h. Отсюда h =. Находим
| |= = 3 = 27.
Поэтому h = 9. Это совпадает с ранее найденным ответом.
Точку D можно найти, как ближайшую к A точку прямой BC, используя методы дифференциального исчисления. Пусть M (t) – произвольная точка прямой BC; её координаты определяются системой (*):
M (–3 + 4 t, 8 – 7 t, 4 – 4 t).
Находим квадрат расстояние от точки A до M (t):
h 2(t) = (9 + 3 – 4 t)2 + (5 – 8 + 7 t)2 + (1 – 4 + 4 t)2
= (12 – 4 t)2 + (–3 + 7 t)2 + (–3 + 4 t)2 =
= 144 – 96 t + 16 t 2 + 9 – 42 t + 49 t 2 + 9 – 24 t + 16 t 2 =
= 81 t 2 – 162 t + 162.
Найдем наименьшее значение функции h 2(t) с помощью производной:
h 2(t) = 162 t – 162; h 2(t) = 0 Þ t = 1.
Подставляем это значение t в уравнение прямой BC и находим, что D (1, 1, 0) является ближайшей к A точкой на прямой BC.
9. Исследовать взаимное расположение следующих пар плоскостей (пересекаются, параллельны, совпадают). Если плоскости пересекаются, то найдите угол между ними, если параллельны – расстояние между ними.
а). p1: 2 y + z + 5 = 0, p2: 5 x + 4 y – 2z +11 = 0.
Решение. Если плоскости p1 и p2 заданы своими общими уравнениями
a 1 x + b 1 y + c 1z + d 1= 0, a 2 x + b 2 y + c 2z + d 2= 0,
то
p1½½ p2 Û = = ¹,
p1 = p2 Û = = =.
В нашем случае ¹ ¹, поэтому плоскости не параллельны и не совпадают. Значит, они пересекаются. Угол между плоскостями вычисляется по формуле
cos a =,
где и – векторы нормали к этим плоскостям. В нашем случае
(0, 2, 1), (5, 4,–2), · = 0·5 + 2· 4 + 1·(–2);
|| = =, || = = 3.
Значит, cos a = =.
Ответ: a = arccos.
б) p1: x – y + 2z + 8 = 0,
p2: 2 x – y + 4z –12 = 0.
Решение. Проверяем на параллельность или совпадение:
Значит, p1½½ p2 но p1 ¹ p2. Расстояние от точки A (x, y, z) до плоскости, заданной уравнением 
находится по формуле
h =.
Выберем точку А Îp1. Для этого надо подобрать любые три координаты, удовлетворяющие уравнению p1. В нашем случае, самое простое: A o(0, 8, 0). Расстояние от A o до p2 и будет расстоянием между p1 и p2 :
h = =.
10. Составить уравнение плоскости p, которая делит пополам тот из двугранных углов между плоскостями
p1: 2 x – y + 2= 0, p2: 5 x + 4 y – 2 z –14 = 0,
который содержит данную точку А (0, 3,–2). Составить параметрическое уравнение прямой l = p 1I p 2 ;
Решение. Если точка 
лежит на плоскости p, которая делит двугранный угол пополам, то расстояния h 1 и h 2 от этой точки до p1 и до p2 равны.
Находим эти расстояния и приравниваем их:
=
Модули мы можем раскрывать с одинаковыми или разными знаками. Поэтому можем получить 2 ответа, т.к. p1 и p2 образуют два двугранных угла. Но в условии требуется найти уравнение плоскости, которая делит пополам тот угол, в котором находится точка А. Значит координаты точки М при подстановке в левые части уравнений данных плоскостей p 1 и должны такие же знаки, что и координаты точки А. Легко проверить, что эти знаки для p1 и «+» для p2 . Поэтому мы раскрываем первый модуль со знаком «–», а второй – со знаком «+»:
=,
3(-2 x + y - 2) = 5 x + 4 y – 2 z –14,
p:11 x + y - 2 z - 14 = 0.
Для того, чтобы составить уравнение прямой l, нам нужно найти направляющий вектор этой прямой и точку на ней.
Из уравнений p1 и p2 находим координаты векторов нормали к этим плоскостям: (2,–1, 0), (5, 4,–2). Направляющий вектор прямой l перпендикулярен и. Такой можно найти с помощью векторного произведения (по определению, если = ´ , то ^ и ^ ):
i j k
= ´ = 2 –1 0 = 2 i + 4 j + 13 k .
5 4 –2
Для того, чтобы найти координаты одной точки на прямой, мы должны найти частное решение системы уравнений
Поскольку уравнений два, а неизвестных три, то система имеет бесконечное количество решений. Нам достаточно подобрать одно. Проще всего положить x = 0 и тогда находим
Þ z = – 3, 
.
Каноническое уравнение прямой, проходящей через точку B (x o, y o, z o) параллельно вектору (a 1, a 2, a 3), имеет вид:
= =.
В нашем случае имеем уравнение:
l: = =.
Ответ: p: 11 x + y – 2 z = 0, l: = =.
11. Даны уравнения двух прямых в пространстве:
x = –1 – t, x = –3 + 2 t ¢,
l 1: y = 6 + 2 t, l 2: y = –2 – 3 t ¢,
z = 5 + 2 t, z = 3 – 2 t ¢.
Доказать, что данные прямые скрещиваются и составить уравнение их общего перпендикуляра.
Решение. Из уравнений прямых находим координаты их направляющих векторов: (–1, 2, 2), (2,–3,–2) и точек A (–1, 6, 5)Î l 1 , B (–3,–2, 3) Î l 2 . Проверяем и на коллинеарность:
= =. 
Значит и l 1 l 2. Следовательно, прямые l 1 и l 2 либо скрещиваются, либо пересекаются. Мы найдем расстояние между ними, и, если оно не равно нулю, то прямые скрещиваются.
Расстояние вычисляется по формуле
d =.
Находим
I j k
´ = –1 2 2 = 2 i + 2 j – k; |´ |= = 3.
2 –3 –2
(– 2,– 8,–2), = – 2·2 – 8·2 – 2·(–1) = –18, d =.
Вектор = ´ перпендикулярен и перпендикулярен. Сле-довательно, ^ l 1 и ^ l 1, а значит, является направляющим вектором общего перпендикуляра 
к этим прямым. Мы уже нашли его коор-динаты: (2, 2,–1). Для того, чтобы
составить уравнение h нам нужно найти координаты одной точки на этой прямой. Для этого мы составим уравнение плоскости π, проходящей через l 1 и h. Для нее векторы, будут направляющими, и A Îp.
x – 1 y – 2 z – 1
–1 2 2 = 0.
2 2 –1
– 6(x – 1) + 3( y – 2) – 6(z – 1) = 0.
– 2(x – 1) + ( y – 2) – 2(z – 1) = 0.
p: –2 x + y – 2 z + 2 = 0.
Находим точку пересечения l 2 и π . Для этого из уравнения l 2 подставляем в уравнение π:
–2(–3 + 2 t ¢) –2 + 3 t ¢ – 2(3 – 2 t ¢) + 2 = 0,
6 – 4 t ¢ – 2 – 3 t ¢ – 6 – 4 t ¢ + 2 = 0,
–7 t ¢= 0, t ¢= 0.
Подставляем найденное t ¢ в уравнение l 2 и находим, что B (–3,–2, 3) и есть общая точка l 2 и π. Имея точку на h и направляющий вектор этой прямой составляем ее уравнение:
.
Заметим, что прямую h можно задать как пересечение двух плоскостей: плоскости π и плоскости π1, проходящей через прямую l 2 с направляющим вектором. Этот способ решения также допускается, и он несколько короче.
Второй способ решения этой задачи использует методы дифференциального исчисления. Общий перпендикуляр к двум скрещивающимся прямым – это кратчайший из отрезков, соединяющих две точки на этих прямых. Находим квадрат расстояния от произвольной точки прямой l 1 до произвольной точки прямой l 2:
h 2(t, t ¢) = (–3 +2 t ¢ + 1 + t )2 + (–2 – 3 t ¢ – 6 – 2 t)2 + (3 – 2 t ¢ – 5 – 2 t)2 =
= (t +2 t ¢ – 2)2 + (8 + 2 t + 3 t ¢)2 + (2 + 2 t + 2 t ¢)2 .
Найдем точку минимума функции h 2(t, t ¢). Для этого вычисляем частные производные и приравниваем их к нулю:
h 2(t, t ¢) = 2(t +2 t ¢ – 2) + 4(8 + 2 t + 3 t ¢) + 4(2 + 2 t + 2 t ¢) = 2(9 t +12 t ¢ + 18);
h 2(t, t ¢) = 4(t +2 t ¢ – 2) + 6(8 + 2 t + 3 t ¢) + 4(2 + 2 t + 2 t ¢) = 2(12 t +17 t ¢ + 24);
9 t +12 t ¢ + 18 = 0 t = –2
12 t +17 t ¢ + 24 = 0 t ¢ = 0.
Подставляем эти значения t и t ¢ в уравнения l 1 и l 2 соответственно и находим, что C (1, 2, 1) и B (–3,–2, 3) являются концами общего перпендикуляра. Остается составить уравнение прямой, проходящей через две точки B и C.
12. Дано уравнение сферы S:
x 2 + y 2 + z 2 +12 x -10 y – 4 z -176 = 0.
а) Составить уравнение плоскости p, проходящей через точки A (–3, 7, 1), B (–1, 9, 2), C (–3, 6, 6)
б) найти координаты центра и радиус окружности, по которой p пересекает S.
Решение. Найдем два вектора параллельных плоскости: (2, 1, 1), (0,–1, 5). Уравнение плоскости, проходящей через данную точку A (x o, y o, z o) параллельно двум данным векторам (a 1, a 2, a 3), (b 1, b 2, b 3) имеет вид
x – x o y – y o z – z o
a 1 a 2 a 3 = 0.
b 1 b 2 b 3
Подставляем в это уравнение наши данные:
x + 3 y – 7 z – 1
2 2 1 = 0.
0 –1 5
Раскрываем определитель:
Найдем координаты центра O ¢ и радиус 
сферы. Для этого выделим полные квадраты:
(x 2 –12 x + 36) – 36 + ( y 2 +10 y + 25) + (z 2 + 4 z + 4) – 4 –176 = 0,
(x – 6)2 + (y – 5)2 + (z + 2)2 = 241.
Значит, O ¢(6,–5,–2), R =.
Центр окружности, получающейся в сечении сферы плоскостью, является основанием перпендикуляра , опущенного из центра сферы на плоскость. Из уравнения плоскости находим, что вектор (11,–10,–2) является вектором нормали к плоскости. Этот же вектор будет направляющим для прямой 
. Параметрическое уравнение прямой, проходящей через данную точку A (x o, y o, z o) с направляющим вектором (a 1, a 2, a 3) имеет вид
x = x o + a 1 t ,
y = y o + a 2 t ,
z = z o + a 3 t .
В нашем случае получаем уравнение:
x = 6 + 11 t ,
l: y = –5 – 10 t ,
z = –2 – 2 t .
Найдем основание перпендикуляра. Это точка пересечения прямой с плоскостью p. Для этого мы должны решить совместно уравнения и p. Подставляем из уравнения l в уравнение π:
11(6 + 11 t) – 10(–5 – 10 t) – 2(–2 – 2 t) + 105 = 0,
66 + 121 t + 50 + 100 t + 4 + 4 t + 105 = 0,
225 t = –225, t = –1.
Найденное t подставляем в уравнение l и находим координаты центра окружности: O ²(–5, 5, 0). Находим длину отрезка O ¢ O ² как расстояние между точками:
½ O ¢ O ²½= = 15.
По теореме Пифагора
r 2 = R 2 –½ O ¢ O ²½2 = 241– 225 = 16.
Значит, r = 4 – радиус окружности.
Ответ: r = 4, O ²(–5, 5, 0).
