Плоскость p в пространстве можно задать
а) с помощью точки A oÎ p и ненулевого вектора ^p; тогда можем написать, что p ={ M ½ ^}; (*)
б) с помощью точки A o Î l и двух неколлинеарных векторов и, параллельных p;
в) с помощью трех точек A o, A 1, A 2Î p , не лежащих на одной прямой.
Теорема 4. 1. Плоскость p, проходящая через точку A o(x o, y o, z o), перпендикулярно вектору (A, B, C), задается в декартовой СК уравнением
A (x – x o) + B (y – y o) + C (z – z o) = 0. (21)
2. Плоскость p, проходящая через точку A o(x o, y o, z o), параллельно двум неколлинеарным векторам изадается уравнением
 |
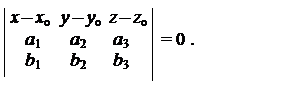(22)
3. Плоскость p, проходящая через три точки A o(x o, y o, z o), A 1(x 1, y 1, z 1), A 2(x 2, y 2, z 2), не лежащие на одной прямой задается уравнением
 |
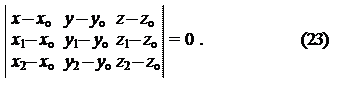4. Плоскость p, отсекающая на координатных осях ненулевые отрезки a, b, c задается уравнением
+ + = 1 (24)
(предполагается, что a, b, c могут быть отрицательными).
Доказательство. 1. Пусть M (x, y, z) – произвольная точка плоскости. Тогда ^ Û · = 0. Поскольку (x – x o, y – y o, z – z o), то последнее равенство в координатах как раз имеет вид (22).
Обратно, если координаты точки M (x, y, z) удовлетворяют (21), то ^ Û M Îp.
2. Пусть M (x, y, z) – произвольная точка плоскости. Тогда компланарен векторам и, а это равносильно тому, что смешанное произведение этих трех векторов равно нулю: = 0. В координатах последнее равенство как раз имеет вид (22).
Обратно, если координаты точки M (x, y, z) удовлетворяют (22), то векторы, , компланарны, а значит M Îp.
3. Если плоскость проходит через три точки A o(x o, y o, z o), A 1(x 1, y 1, z 1), A 2(x 2, y 2, z 2), не лежащие на одной прямой, то векторы (x 1– x o, y 1– y o, z 1– z o) и (x 2 – x o, y 2 – y o, z 2 – z o) неколлинеарны друг другу и параллельны плоскости p. Подставим их координаты в (22) вместо координат векторов и, и получим (23).
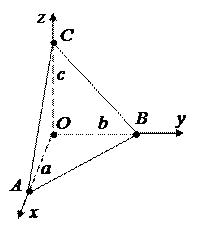4. Условие означает, что плоскость проходит через точки A (a, 0, 0), B (0, b, 0), C (0, 0, c). Подставим их координаты в уравнение (23):
x – a y –0 z –0
0 – a b –0 0 –0 = 0.
0 – a 0 –0 c –0
Самостоятельно раскройте определитель и приведите получившееся уравнение к виду (24).
Это уравнение называется уравнением плоскости в отрезках.
Следствие. Любая плоскость определяется уравнением вида
Ax + By + Cz + D = 0, (25)
которое называется общим уравнением плоскости. И обратно, всякое уравнение вида (25) определяет плоскость.
Доказательство. Любая плоскость может быть задана с помощью точки и вектора нормали, а значит ее можно задать уравнением вида (21). Раскроем скобки и обозначим D = –Ax o– By o– Cz o= const. Получим уравнение (25).
Обратно, пусть некоторое множество p определяется уравнением (25). Пусть A o(x o, y o, z o) – произвольная точка этого множества. Тогда ее координаты удовлетворяют (25):
Ax o+ By o+ Cz o+ D = 0.
Отсюда D = –Ax o– By o– Cz o, и подставляя это значение в (25) получим (21). А это уравнение, как уже известно, задает плоскость.
Рассмотрим различные частные случаи плоскостей, задаваемых уравнениями вида (25).
1. D = 0. Тогда уравнению
Ax + By + Cz = 0
удовлетворяют координаты точки O (0, 0, 0).
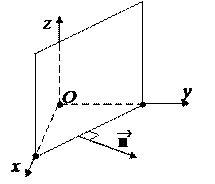Плоскость проходит через начало координат.
2. C = 0.Имеем уравнение
Ax + By + D = 0.
Тогда вектор нормали к плоскости – (A, B, 0) и ^ Oz, а значит, p½½ Oz.
Аналогично, при B = 0 получим p½½ Oy, а при A = 0 – p½½ Ox.
3. A = B = 0. Имеем уравнение
Cz + D = 0,
которое равносильно z = – C /D. Тогда
p^ Oz.
Аналогично, при A = C = 0 будет
p ^ Oy, а при B = C = 0 – p ^ Ox.
