Определение. Кривой второго порядка называется геометрическое место точек, координаты которых удовлетворяют уравнению
а 11 х 2 + 2 а 12 ху + а 22 у 2 + 2 а 1 х + 2 а 2 у + с = 0, (8)
в котором хотя бы один из коэффициентов а 11, а 12, а 22 отличен от нуля. Выражение
а 11 х 2 + 2 а 12 ху + а 22 у 2
называется квадратичной часть уравнения, 2 а 1 х + 2 а 2 у – линейной частью, а с – свободным членом.
Если мы перейдем к новой СК Ox ¢ y ¢, то формулы замены координат будут иметь вид
x = a x ¢ + b y ¢ + b 1,
y = g x ¢ + d y ¢ + b 2.
Если мы подставим эти выражения в (8), то снова получим уравнение такого же вида, т.е. содержащее x ¢ и y ¢ во второй степени. Поэтому наше определение корректно, т.е не зависит от выбора СК. В дальнейшем, СК всегда предполагается декартовой.
Определение. Точка O ¢ называется центром кривой второго порядка, если она является ее центром симметрии. Кривая, которая имеет центр, называется центральной.
Предположим, что СК выбрана так, что ее начало находится в центре кривой. Тогда одновременно с точкой M (x, y) кривой будет принадлежать и точка M ¢(– x,– y). Подставим ее координаты в (7) и получим
а 11 х 2 + 2 а 12 ху + а 22 у 2 – 2 а 1 х – 2 а 2 у + с = 0. (8¢)
Вычтем из равенства (8) равенство (8¢):
4(а 1 х + а 2 у) = 0.
И это должно выполняться для любой точки M (x, y) на кривой. Поэтому а 1 = а 2 = 0, если начало координат находится в центре. Поэтому, если изначально начало координат не находится в центре O ¢, то мы совершим параллельный перенос координатных осей в центр, и уравнение кривой в новой СК O ¢ х ¢ у ¢ примет вид
а 11 х ¢2 + 2 а 12 х ¢ у ¢ + а 22 у ¢2 + с ¢ = 0, (9)
т.е. линейная часть уравнения исчезнет. При этом, коэффициенты квадратичной части останутся прежними; это будет установлено в процессе доказательства следующей теоремы.
Теорема 5. Координаты (x o, y o) центра кривой, заданной уравнением (8), находятся из системы линейных уравнений
а 11 х o + а 12 у o + а 1 = 0,
а 12 х o + а 22 у o + а 2 = 0.
Доказательство. Введем новую декартову СК O ¢ х ¢ у ¢, которая получается из Oху переносом начала в центр O ¢(x o, y o) кривой. Тогда формулы замены координат имеют вид:
x = x ¢ + х o,
y = y ¢ + у o.
Подставим эти формулы в (7):
а 11(x ¢+ х o)2 + 2 а 12 (x ¢+ х o)( y ¢+ y o) + а 22(y ¢+ y o)2 +
+ 2 а 1(x ¢+ х o) + 2 а 2(y ¢+ y o) + с = 0.
После преобразований получаем
а 11(x ¢)2 + 2 а 12 x ¢ y ¢+ а 22(y ¢)2 + 2(а 11 х o+ а 12 у o+ а 1) x ¢+
+ 2(а 12 х o+ а 22 у o+ а 2) y ¢+ с ¢= 0,
где с ¢ = j(x o, y o) – значение левой части уравнения (7) в точке O ¢. Поскольку в новой СК коэффициенты при x ¢ и y ¢ должны быть равны нулю, то получаем (10).
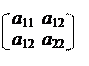Заметим, что уравнение кривой в новой СК можно выписать, не совершая подстановки (11) и преобразований: коэффициенты квадратичной части не изменяются, надо только вычислить с ¢.
Обозначим A = – матрица квадратичной части уравнения (8) (она же является матрицей системы линейных уравнений (10)),
d = det A, dx = –, dy = –.
1 случай. d ¹ 0. Тогда по правилу Крамера система (10) имеет единственное решение
x o= dx/d, y o= dy /d, (*)
а кривая имеет единственный центр. Минусы были поставлены выше потому, что а 1 и а 2 находятся в (10) не в правой части, а в левой.
2 случай. d = 0, dx¹ 0 и dy¹ 0 (заметим, что в случае d = 0, определители dx и dy будут равны или неравны нулю только одновременно). Тогда ранг расширенной матрицы системы (10) будет равен 2, а rank A =1. Значит, согласно теореме Кронекера-Капелли система (10) не имеет решений, а кривая не имеет центра.
3 случай. d = 0, dx = dy = 0. Тогда оба уравнения в (10) пропорциональны, а значит, эта система имеет бесконечное количество решений, а кривая – бесконечное количество центров.
Упростим еще величину с ¢:
с ¢ = j(x o, y o) = а 11 х o2 + 2 а 12 х o у o + а 22 у o2 + 2 а 1 х o + 2 а 2 у o + с =
= (а 11 х o + а 12 у o + а 1) х o+ (а 12 х o + а 22 у o + а 2) у o + а 12 х o + а 22 у o + с.
В силу (9) выражения в скобках равны нулю, и мы имеем
с ¢ = а 1 х o + а 2 у o + с. (12)
Подставляя сюда (*) получаем
с ¢ = а 1 + а 2 + с = (а 1dx + а 2 dy + с) =, (13)
где
а 11 а 12 а 1
D = а 12 а 22 а 2.
а 1 а 2 с
В скобках как раз стоит разложение D по последней строке или последнему столбцу. Равенство (13) позволяет выписать (9) не находя координат центра кривой. Но, если уже центр найден, то легче вычислить с ¢ по формулам (12).
