Напомним, что углом между скрещивающимися прямыми называется угол между параллельными им прямыми, проходящими через одну точку. Другими словами, если прямые l o и l 1 скрещиваются, то мы должны совершить параллельный перенос прямой l o, так чтобы получилась прямая l o¢, пересекающаяся с l 1, и измерять угол между l o¢ и l 1.
Две скрещивающиеся прямые имеют единственный общий перпендикуляр. Его длина называется расстоянием между прямыми.
Пусть две прямые в пространстве заданы своими каноническими уравнениями:
l o: = =, l 1: = =. (35)
Тогда сразу можем сделать вывод, что (a 1, a 2, a 3)½½ l o, (b 1, b 2, b 3)½½ l 1, A o(x o, y o, z o)Î l o, A 1(x 1, y 1, z 1)Î l 1. Составим матрицу
x 1– x o y 1– y o z 1– z o
A = a 1 a 2 a 3,
b 1 b 2 b 3
и пусть D = det A.
Теорема 8. 1. Угол между l и p вычисляется по формуле
cos a = =. (36)
2. Прямые l o и l 1 скрещиваются Û D ≠ 0.
3. Прямые l o и l 1 пересекаются Û D = 0 и не коллинеарен.
4. l o½½ l 1 Û rank A = 2 и ½½.
5. l o= l 1 Û rank A = 1.
Доказательство. 1. Угол a между прямыми l o и l 1 может быть равен углу b между их направляющими векторами, , а может быть смежным с ним. В первом случае
cos a = cos b =,
а во втором случае
cos a = – cos b =½ cos b½ =.
Эта формула подойдет и к первому случаю. Обратите внимание, что на чертеже изображена не прямая l o, а параллельная ей прямая l o¢.
2, 3. Очевидно, что прямые l o и l 1 не параллельны тогда и только тогда, когда их направляющие векторы и не коллинеарны. При этом, прямые лежат в одной плоскости и пересекаются Û векторы, , компланарны Û их смешанное произведение равно нулю: = 0. А в координатах это произведение точности равно D.
Соответственно, если D ≠ 0, то векторы,, не компланарны, а значит, прямые l o и l 1 не лежат в одной плоскости Þ они скрещиваются.
4, 5. Если l o½½ l 1 или l o= l 1, то ½½ . Но в первом случае вектор неколлинеарен и, и поэтому первая строка в матрице A непропорциональна второй и третей строкам. Значит, rank A = 2.
Во втором случае все три вектора, , коллинеарны друг другу, и поэтому, все строки
в матрице A пропорциональны. Значит, rank A = 1.
И обратно, если ||, то прямые l o и l 1 параллельны или совпадают; при этом, вторая и третья строки матрицы A пропорциональны. Если, при этом, rank A = 2, то первая строка матрицы непропорциональна второй и третьей, а значит, вектор неколлинеарен и Û l o|| l 1. Если же rank A = 1, то все строки в матрице A пропорциональны, а значит, все три вектора ,, коллинеарны друг другу Û l o= l 1.
Теорема 9. Пусть две прямые l o и l 1 в пространстве заданы своими каноническими уравнениями (35). Тогда
1. если l o½½ l 1, то расстояние между l o и l 1 находится по формуле
h =, (37)
2. если l o и l 1 скрещиваются, то расстояние между ними находится по формуле
h =. (38)
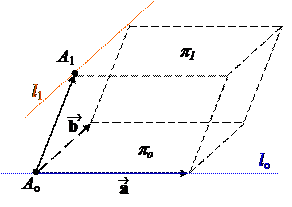Доказательство. 1. Пусть l o½½ l 1. Отложим вектор от точки A o, и на векторах и построим параллелограмм. Тогда его высота h будет расстоянием между l o и l 1. Площадь этого параллелограмма: S =½ ´½, а основание равно ½ ½. Поэтому
h = S/ ½ ½ = (37).
2. Пусть l o и l 1 скрещиваются. Проведем через прямую l o плоскость po½½ l 1, а через прямую l 1 проведем плоскость p1½½ l o.
Тогда общий перпендикуляр к l o и l 1 будет общим перпендикуляром к po и p1. Отложим векторы и из точки A o и на векторах, и построим параллелепипед. Тогда его нижнее основание лежит в плоскости po, а верхнее – в плоскости p1. Поэтому высота параллелепипеда будет общим перпендикуляром к po и p1, а ее величина h будет расстоянием между l o и l 1. Объем параллелепипеда равен ½ ½, а площадь основания – ½´½ Þ
h = V/S осн = (38).
Следствие. Расстояние от точки A 1(x 1, y 1, z 1) до прямой l, заданной уравнением
l: = =
вычисляется по формуле (37).
Примеры решения задач.
1. Даны координаты вершин A (1,– 6), B (–3, 0), C (6, 9) треугольника ABC. Составить уравнение окружности описанной вокруг треугольника.
Решение. Для того, чтобы составить уравнение окружности нам необходимо знать ее радиус R и координаты центра О (a, b). Тогда уравнение выглядит так:
(x – a)2 +(y – b)2 = R 2.
Центр окружности, описанной вокруг треугольника находится на пересечении серединных перпендикуляров к сторонам этого треугольника. Находим координаты середин M 1(x 1, y 1), и M 3(x 3, y 3) сторон BC и AB соответственно:
x 1= = =, y 1= = =, M 1.
Аналогично M3(–1,–3).
Пусть l 3 – прямая, являющаяся серединным перпендикуляром к AB, а l 1 – к BC. Тогда = (– 4, 6) ^ l 3 и l 3 проходит через M 3 . Поэтому ее уравнение:
– 4(x +1) + 6(y +3) = 0.
Аналогично = (9, 9) ^ l 3. Поэтому уравнение l 1:
9(x - ) + 9(y -) = 0
x + y – 6 = 0.
Имеем О = l 1 I l 3. Поэтому, чтобы найти координаты точки О необходимо решить совместно уравнения l 1 и l 3 :
x + y – 6 = 0,
– 4 x + 6 y +14 = 0.
Прибавим ко второму уравнению первое, умноженное на 4:
x + y – 6 = 0,
10 y – 10 = 0.
Отсюда y = 1, x = 5, O (5, 1).
Радиус равен расстоянию от О до любой из вершин треугольника. Находим:
R =½½= =.
Значит уравнение окружности:
(x – 5)2 + (y –1)2 = 65.
2. В прямоугольном треугольнике ABC известныуравнение одного из катетов 3 x – 2 y + 5 = 0, координаты вершины C (–5,–5) и координаты середины O (–3/2,–3) гипотенузы AB. Найти координаты
вершин A, B и координаты точки E, симметричной O относительно стороны BC. Найти координаты точки пересечения медиан треугольника ABC.
Решение. Пусть катет, уравнение которого нам дано, – это СВ. Он задан общим уравнением вида
ax + by + c = 0.
В данном уравнении геометрический смысл
коэффициентов a и b – это координаты вектора нормали (a, b). Поэтому (3,-2)^ ВС.
Составим уравнение перпендикуляра l = OD к стороне СВ и найдем координаты точки D. Вектор будет параллелен OD, т.е. он является направляющим вектором этой прямой. Кроме этого, нам известны координаты точки О на этой прямой. Составляем параметрическое уравнение l:
x = – + 3 t, (*)
y = – 3 - 2 t.
Имеем D = l I BC. Поэтому, для того, чтобы найти координаты этой точки мы должны решить совместно уравнения l и BC. Подставляем x и y из уравнения l в уравнение BC:
3(– + 3 t) –2(–3 -2 t)+5 = 0,
– + 9 t +6 +4 t +5 = 0,
13 t = –, tD = –.
Подставляем найденное t в уравнение l и находим координаты точки D (–3,–2). Для того, чтобы найти координаты E вспомним физический смысл параметрического уравнения прямой: оно задает прямолинейное и равномерное движение. В нашем случае, начальная точка – это О, вектор скорости – это. Отрезок ОE вдвое длиннее отрезка ОD. Если за время tD = – мы прошли путь от О до D, то путь от О до E мы пройдем за время tE = 2 tD = –1. Подставляя это значение в (*), находим E (– 4,5;–1).
