В этом параграфе для удобства изложения будем считать, что совпадающие прямые – это частный случай параллельных.
Пусть две прямые на плоскости заданы общими уравнениями:
l 1: A 1 x + B 1 y + C 1 = 0 ,
l 2: A 2 x + B 2 y + C 2 = 0 .
Тогда мы сразу можем сделать вывод, что (A 1, B 1) и (A 2, B 2) – это векторы нормали к l 1 и l 2.
Теорема 2. 1. l 1½½ l 2 и l 1¹ l 2 Û = ¹.
2. l 1= l 2 Û = =.
3. l 1^ l 2 Û A 1 A 2 + B 1 B 2 = 0.
4. угол между l 1 и l 2 вычисляется по формуле
cos a = =. (16)
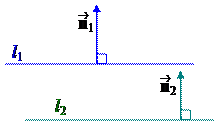Доказательство. 1, 2. Очевидно, что l 1½½ l 2 Û ½½, а по второму признаку коллинеарности векторов это равносильно
= = l. (*)
При этом, прямые будут совпадать Û у них есть общая точка M o(x o, y o), т. е. если одновременно выполняется
A 1 x o + B 1 y o + C 1 = 0,
A 2 x o + B 2 y o + C 2 = 0.
Вычтем из первого равенства второе, домноженное на l:
(A 1– l A 2) x o + (B 1– l B 2) y o + C 1– l C 2 = 0.
В силу (*) обе скобки равны нулю Þ C 1– l C 2 = 0 Û C 1/ C 2 = l. (**) Объединяя (*) и (**), получаем требуемый результат.
Обратно, если выполнено условие пункта 2, то уравнения прямых l 1 и l 2 пропорциональны, т.е., разделив первое уравнение на некоторое число l, мы получим второе уравнение. Значит эти уравнения равносильны и определяют на плоскости одно и то же множество.
3, 4. Напомним, что углом между двумя прямыми называется меньший из двух углов, которые образуются при их пересечении. Таким образом, угол a между прямыми находится в пределах 0 £ a £ p/2.
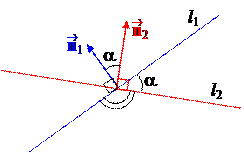Пусть b =Ð(,). Тогда 0 £ b £ p.
Очевидно, что b совпадает с одним из двух углов, которые образуют прямые при пересечении.
1 случай: 0 £ b £ p/2. Тогда a = b Þ
cos a = cos b =.
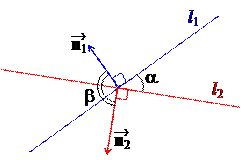
2 случай: p/2 < b £ p. Тогда a = p – b и cos b < 0 Þ
cos a = cos (p – b) = – cos b =
=½ cos b½ = .
Эта формула подойдет и к первому
случаю: неотрицательную величину модулем не испортишь. Последнее равенство в (16) – эта та же формула, только расписанная в координатах. В частности, из (16) следует, что l 1^ l 2 Û · = 0 Û A 1 A 2 + B 1 B 2 = 0.
Упражнение 1. Прямые на плоскости могут быть заданы не только общим уравнением. После изучения темы «Взаимное расположение прямой и плоскости» вы легко напишите условия параллельности и совпадения двух прямых, одна из которых задана каноническим или параметрическим уравнением, а вторая – общим уравнением.
Упражнение 2. Самостоятельно напишите условия параллельности и совпадения двух прямых, заданных уравнениями с угловым коэффициентом.
Теорема 2. Пусть две прямые на плоскости заданы уравнениями с угловым коэффициентом
l 1: y = k 1 x + q 1, l 2: y = k 2 x + q 2.
Тогда угол между ними вычисляется по формуле
tg q =.
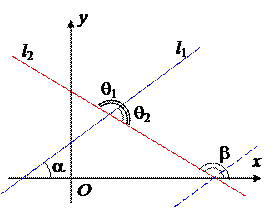
Доказательство. Пусть k 1= tg a1, k 2 = tg a2 , а q1 и q2 – углы, которые образуются при пересечении прямых (см. чертеж). Тогда q1= b – a, и, если q1£ p/2, то он будет считаться углом между l 1и l 2. В этом случае tg q1³ 0.
Находим:
tg q1= tg(b – a) = =.
Если q1> p/2, то между прямыми считается q2 = p – q1. Тогда
tg q2 = tg(p – q1) = – tg q1=½tg q1½ =.
Эта формула подойдет и к первому случаю.
Заметим, что если убрать в числителе модуль, то получится формула, по которой можно вычислить ориентированный угол от l 1 до l 2, (отсчитываемый против часовой стрелки). Данный угол может находиться в пределах – p £ q £ p.
