Например, на рис. 87 точка с проекциями К" и К' принадлежит прямой АВ, а
точка с проекциями L" и L' принадлежит прямой CD. Эти точки одинаково
удалены от пл. 2, но расстояния их от пл., различны: точка с проекциями
L" и L' дальше от nt, чем точка с проекциями К" и К' (рис. 88).
Точки с проекциями ", ' и ", ' одинаково удалены от пл. 1, но
Расстояния этих точек от пл. 2 различны.
Точка с проекциями L" и L', принадлежащая прямой CD, закрывает собой
точку с проекциями К" и К' прямой АВ по отношению к пл. ^ соответствующее
направление взгляда показано стрелкой у проекции L". По отношению к пл. 2
точка с проекциями " и ' прямой CD закрывает собой точку с проекциями М" и
М' прямой АВ; направление взгляда указано стрелкой внизу, у проекции N'.
Обозначения проекций "закрытых" точек помещены в скобках1).
О ПРОЕКЦИЯХ ПЛОСКИХ УГЛОВ
1. Если плоскость, которой расположен некоторый угол, перпендикулярнак плоскости проекций, то он проецируется на эту плоскость проекций видепрямой линии. 2. Если плоскость прямого угла не перпендикулярна к плоскости проекцийи хотя бы одна его сторона параллельна этой плоскости, то прямой уголпроецируется на нее в виде прямого же угла. Положим, что сторона СВ прямого угла АСВ (рис. 89) параллельнаплоскости проекций. В таком случае прямая СВ параллельна Ѱ°. Пусть втораясторона (АС) прямого угла пересекает свою проекцию А°С° в точке К. Проводимв плоскости проекций через точку К прямую параллельно Ѱ°. Прямая KL такжепараллель- ') Для точек, принадлежащих скрещивающимся прямым и расположенных наодной и той же проецирующей прямой, встречается название "конкурирующие". 37 на СВ, и угол CKL получается прямым. Согласно теореме о трехперпендикулярах угол C°KL -- также прямой1). Следовательно, иугол А°С°В° -- прямой. Этой теореме о проецировании прямого угла соответствуют две обратные(пп. 3 и 4). 3. Если проекция плоского угла представляет собой прямой угол, топроецируемый угол будет прямым лишь при условии, что по крайней мере одна изсторон этого угла параллельна плоскости проекций. 4. Если проекция некоторого угла, у которого одна сторона параллельнаплоскости проекций, представляет собой прямой угол, то проецируемый уголтоже прямой
Рис. 91 Рис. 92 На основании изложенного можно установить, что углы, изображенные нарис. 90, в пространстве прямые. В каком случае проекции прямого угла на двух плоскостях проекцийпредставляют собой прямые утлы? Это бывает, когда одна сторона прямого углаперпендикулярна к третьей плоскости проекций (тогда другая его сторонапараллельна этой плоскости). Призер дан на рис. 91: сторона АСперпендикулярна к 3, сторона ВС параллельна 3. Пользуясь сведениями о·проецировании прямого угла, о дополнении системыя,, 2 системой 4,, (8) и о расположении проекций прямой, параллельнойодной из плоскостей проекций (11), мы можем выполнить следующеепостроение: провести через некоторую точку А прямую так, чтобы она пересекладанную прямую под углом 90°. Решение показано на рис. 92, где слева даноисходное положение, в середине показано образование, кроме си- ') Согласно прямой теореме о трех перпендикулярах: если KL+C°K, то KLJLС К. Согласно обратной теореме: если K.LLCK, то KLJ-C°K. 2) Интересующихся доказательством обратных теорем отсылаем кпредыдущим изданиям книги. 38 стемы 1, 2, еще одной системы 4, 1, причем пл. 4%ВС, а справавыполнено построение прямой AKLBC. Так как пл. 4% ВС, что обеспечивается проведением оси 4/ 1,параллельно B'C', то прямой угол АКВ (или АКС) проецируется на пл. 4 в видепрямого же угла AIVKIVBIV. Построивпроекции точки A и прямой BC на пл. 4, проводимAIVKIV % BIV CIV, а затемполучаем проекции К' и К" и проекции А'К' и А"К" (ход построения указанстрелками). Можно ли считать, что, построив перпендикуляр АК к прямой BC, мыопределили расстояние от А до BC? Нет, мы только построили проекции отрезкаАК; ни одна из них не определяет величинц расстояния. Если надо определитьвеличину отрезка АК, т. е. расстояние от A до BC, то надо продолжитьпостроение, применив хотя бы способ, изложенный в 13.. · 5. Ecли плоскость тупого или острого угла не перпендикулярна кплоскости проекций и хотя бы одна сторона угла параллельна плоскостипроекций, то проекция тупого угла на эту плоскость представляет собой тупойугол, а проекция острого угла -- острый угол. Предположим, что прямая СВ (рис. 93) параллельна плоскости проекций.Рассмотрим тупой угол КСВ или острый угол МСВ и проведем в плоскости этогоугла прямую CL% СВ. Так как угол LCB-- прямой, то его проекция -- угол LC°B° 
Рис. 93 Рис. 94 представляет собой также прямой угол. Этот угол заключен внутри углаКѰ° и заключает внутри себя угол МѰ°, следовательно, угол КѰ° --тупой, а угол МѰ° -- острый. Таким образом, проекция угла представляетсобой угол с тем же названием (прямой, тупой или острый), что и сам угол,если хотя бы одна сторона угла параллельна плоскости проекций. Вообще жепроекция любого угла может представлять собой или острый, или прямой, илитупой угол, в зависимости от положения утла относительно плоскости проекций. 6. Если обе стороны любого угла, параллельны плоскости проекций, то егопроекция равна по величине проецируемому углу. Это следует из равенства углов с параллельными и одинаковонаправленными сторонами. Поэтому, например, угол между прямой АВ (рис. 50, с. 27) и пл. 2 легкоопределить: это - угол между проекцией А 'В' и осью х; таким же образом уголмежду CD и пл. 1 (рис. 51) определится как угол между C"D" и осью х, уголмежду EF (рис. 52) и пл. 2 -- как угол между E"'F'" и осью z. Для прямого угла равенство между его проекцией и самим углом имеетместо и тогда, когда лишь одна сторона прямого угла параллельна плоскостипроекций. Но для острого или тупого угла, у которого одна сторона параллельнаплоскости проекций, проекция угла не может равняться проецируемому углу. Приэтом проекция острого угла меньше проецируемого угла, а проекция тупогобольше проецируемого угла. Пусть (рис.94) угол А 1ВС -- острый и его сторона СВ параллельна пл. 0; Ѱ° || СВ. Пл., проведенная через точку С перпендикулярно к СВ,перпендикуляр- 39 на к пл. 0, пересекая последнюю по прямой п°, проходящей через С° иперпендикулярной к Ѱ°, Если провести через точку В различные прямые подтем же самым острым углом к прямой СВ, то все эти прямые будут пересекатьпл. в точках, проекции которых расположатся на прямой п°. Положим, чтопрямые АВ и А1В составляют с прямой СВ равные между собой утлы: " ABC = "А1ВС. Если при этом АВ параллельна плоскости 0, то" А°В°С°=" ABC. Если жесторона А 1В не параллельна 0, то проекция точки At получится на прямой и°ближе к С°, чем проекция точки А. Следовательно, проекция угла A1BCпредставляет собой угол, меньший угла А°В°С°, т. е. "А 10°Ѱ< "А1BC 7. Если стороны угла параллельны плоскости проекций или одинаковонаклонены к ней. то деление проекции угла на этой плоскости пополамсоответствует делению пополам и самого угла в пространстве. 8. Деление угла в пространстве пополам соответствует делению пополам иего проекции только при условии, что стороны угла составляют с плоскостьюпроекций равные углы'). 9. Если стороны угла одинаково наклонены к плоскости проекций, тоугол-проекция не может равняться проецируемому углу. Это (рис. 95) можно устаноэить путем совмещения угла MKN с пл. я„при вращении вокруг прямой. При этом угол ° окажется внутри угла МК^,а вершины К„ и К° -- на общем перпендикуляре к. 
Рис. 95 Рис. 96 10. Проекции острого и тупого углов могут равняться проецируемому углуне только при условии параллельности сторон угла плоскости проекций. Из рис.96 видно, что все углы, например острый угол и тупой уголMKNit стороны которых соответственно расположены в проецирующих плоскостях и, имеют своей проекцией угол, равный углу MLN, причем эти углы могутприближаться к 0° и к 180°. Очевидно, среди этих углов может оказаться угол,равный своей проекции. Пример построения такого угла дан в 38. 13) РАЗЛИЧНЫЕ СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ НА ЧЕРТЕЖЕ Положение плоскости в пространстве определяется: а) тремя точками, не лежащими на одной прямой линии, б) прямой иточкой, взятой вне прямой, в) двумя пересекающимися прямыми, г) двумяпараллельными прямыми. В соответствии с этим на чертеже плоскость может быть задана: а) проекциями трех точек, не лежащих на одной прямой (рис. 97), б)проекциями прямой и точки, взятой вне прямой (рис. 98), в) проекциями двухпересекающихся прямых (рис.99), г) проекциями двух параллельных прямых (рис.100). Каждое из представленных на рис. 97--100 заданий плоскости может бытьпреобразовано в другое из них. Например, проведя через точки А и В (рис. 97)прямую, мы получим задание плоскости, представленное на рис. 98; от него мыможем перейти к рис. 100, если через точку С проведем прямую, параллельнуюпрямой АВ.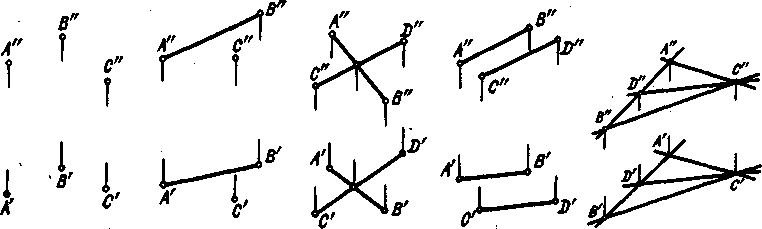 
Рис. 97 Рис. 98 Рис. 99 Рис. 100 Рис. 101 Плоскость может быть задана на чертеже и проекциями любой плоскойфигуры (треугольника, квадрата, круга и т. д.). Пусть некоторая пл. определена точками А, В к С (рис. 101). Проведя прямые линии черезодноименные проекции этих точек, получим проекции треугольника ABC. Точка D,взятая на прямой АВ, тем самым принадлежит, пл,; проводя прямую черезточку D и через другую точку, заведомо принадлежащую пл. (например, черезточку С), получаем еще одну прямую в пл.. Аналогично могут быть построены прямые, а следовательно, и точки,принадлежащие плоскости, заданной любым из перечисленных выше способов. В дальнейшем мы увидим, что плоскость, перпендикулярная к плоскостипроекций, может быть задана прямой, по которой эти плоскости пересекаютсямежду собой.
СЛЕДЫ ПЛОСКОСТИ
Рис. 102 Рис. 103 Рис. 104,' и 2 прямую, получим горизонтальную проекцию линии пересеченияплоскостей и 1|. Линия пересечения плоскостей и 2 определяется фронтальными следамипрямых АВ " СВ. Прямые, по которым некоторая плоскость пересекает плоскости проекций,называются следами этой плоскости на плоскостях проекций или, короче,следами плоскости. На рис. 103 изображена пл. о, пересекающая горизонтальную плоскостьпроекций по прямой, обозначенной h'о и фронтальную плоскость --по прямой f"о. Прямая h'о называется горизонтальнымследом плоскости, прямая f"о -- фронтальным следом плоскости. Если плоскость пересекает ось проекций, то на этой оси получается точкапересечения следов плоскости'). Так, на рис. 103 следы f"о иh'о пересекаются на оси в точке, обозначенной Ха. След плоскости на плоскости проекций сливается со своей проекцией наэтой плоскости. След h'о " hо (рис. 103) сливается со своейгоризонтальной проекцией; фронтальная проекция этого следа располагается наоси проекций. След f"о "fо сливается со своей фронтальнойпроекцией; горизонтальная проекция этого следа располагается на осипроекций. На чертеже плоскость может быть задана проекциями ее следов. Можноограничиться обозначением только самих следов (рис. 104). Такой чертежнагляден и представляет удобства при некоторых построениях. При построении следов плоскости точка их пересечения может бытьиспользована для проверки построения: оба следа должны пересекаться междусобой в точке на оси проекций (см. рис. 102). Угол между следами на чертеже не равен углу, образованному следамиплоскости в пространстве. Действительно, в пересечении следов находитсявершина трехгранного угла, ') Для нее встречается название "точка схода следов". 43 две грани которого совпадают с плоскостями проекций (рис. 103). Носумма двух плоских углов трехгранного угла больше третьего плоского угла.Поэтому угол, образованный следами f"о и h'о начертеже (рис. 104), всегда больше угла между этими следами в пространстве. Если рассматривать плоскость в системе ль 2, 3, то в общем случаеплоскость пересечет каждую из осей проекций (рис. 105: пл. а пересекает осих, у и z). Такая плоскость называется плоскостью общего положения. След "' "р o называется профильным следом плоскости. Так как точки Х„, и " лежат соответственно на осях х, у и z,то для построения чертежа плоскости в системе ль 2, 3 достаточно иметь заданными отрезки ОХК OYa иО2„ т. е. знать координаты точек Х„ У" и Z" в системе осей х, у,z. Дело сводится лишь к Одной координате для каждой из этих точек, так какдве другие координаты равны нулю. Например, для построения точки. надознать лишь ее аппликату: абсцисса и ордината этой точки равны нулю. 
Рис. 105 Рис. 107 
