Проекции центральные и параллельные

Проекции

 

В общем случае проекции преобразуют точки, заданные в системе координат размерностью n, в системы координат размерностью меньше чем n.

Будем рассматривать случай проецирования трех измерений в два. Проекция трехмерного объекта (представленного в виде совокупности точек) строится при помощи прямых проекционных лучей, которые называются проекторами и которые проходят через каждую точку объекта и, пересекая картинную плоскость, образуют проекцию.

 

Рис. 3.7. Центральная и параллельная проекции

Определенный таким образом класс проекций существует под названием плоских геометрических проекций, так как проецирование производится на плоскость, а не на искривленную поверхность и в качестве проекторов используются прямые, а не кривые линии.

Многие картографические проекции являются либо не плоскими, либо не геометрическими.

Плоские геометрические проекции в дальнейшем будем называть просто проекциями.

Проекции делятся на два основных класса (рис. 3.7):

· параллельные (аксонометрические);

· центральные (перспективные).

Полная классификация проекций приведена на рис. 3.8.

Рис. 3.8. Классификация проекций

Параллельные проекции делятся на два типа в зависимости от соотношения между направлением проецирования и нормалью к проекционной плоскости (рис. 3.9.):

1) ортографические – направления совпадают, т. е. направление проецирования является нормалью к проекционной плоскости;

2) косоугольные – направление проецирования и нормаль к проекционной плоскости не совпадают.

 

Рис. 3.9. Ортографические и косоугольные проекции

Наиболее широко используемыми видами ортографических проекций является вид спереди, вид сверху(план) и вид сбоку, в которых картинная плоскость перпендикулярна главным координатным осям. Если проекционные плоскости не перпендикулярны главным координатным осям, то такие проекции называются аксонометрическими.

При аксонометрическом проецировании сохраняется параллельность прямых, а углы изменяются; расстояние можно измерить вдоль каждой из главных координатных осей (в общем случае с различными масштабными коэффициентами).

Изометрическая проекция – нормаль к проекционной плоскости, (а следовательно и направление проецирования) составляет равные углы с каждой из главных координатных осей. Если нормаль к проекционной плоскости имеет координаты (a,b,c), то потребуем, чтобы | a| = |b| = |c|, или ±a=±b=±c, т. е. имеется 8 направлений (по одному в каждом из октантов), которые удовлетворяют этому условию. Однако существует лишь 4 различных изометрических проекции (если не рассматривать удаление скрытых линий), так как векторы (a, a, a) и (-a,-a,-a) определяют нормали к одной и той же проекционной плоскости.

Изометрическая проекция (рис. 3.10.) обладает следующим свойством: все 3 главные координатные оси одинаково укорачиваются. Поэтому можно проводить измерения вдоль направления осей с одним и тем же масштабом. Кроме того, главные координатные оси проецируются так, что их проекции составляют равные углы друг с другом (120°).

 

 

Рис. 3.10. Изометрическая проекция единичного куба

Косоугольные (наклонные) проекции сочетают в себе свойства ортографических проекций (видов спереди, сверху и сбоку) со свойствами аксонометрии. В этом случае проекционная плоскость перпендикулярна главной координатной оси, поэтому сторона объекта, параллельная этой плоскости, проецируется так, что можно измерить углы и расстояния. Проецирование других сторон объекта также допускает проведение линейных измерений (но не угловых) вдоль главных осей. Отметим, что нормаль к проекционной плоскости и направление проецирования не совпадают.

Двумя важными видами косоугольных проекций являются проекции:

· Кавалье (cavalier) – горизонтальная косоугольная изометрия (военная перспектива);

· Кабине (cabinet) – фронтальная косоугольная диметрия.

 

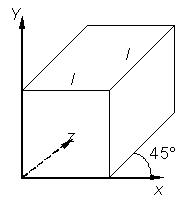
Рис. 3.11. Проекция Кавалье

В проекции Кавалье (рис. 3.11.) направление проецирования составляет с плоскостью угол 45°. В результате проекция отрезка, перпендикулярного проекционной плоскости, имеет ту же длину, что и сам отрезок, т. е. укорачивание отсутствует.

 

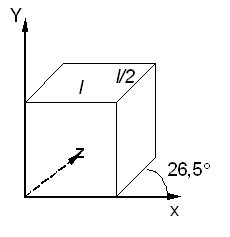
Рис. 3.12. Проекция Кабине

Проекция Кабине (рис. 3.12.) имеет направление проецирования, которое составляет с проекционной плоскостью угол 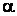= arctg(½) (≈26,5°). При этом отрезки, перпендикулярные проекционной плоскости, после проецирования составляют ½ их действительной длины. Проекции Кабине являются более реалистическими, чем проекции Кавалье, так как укорачивание с коэффициентом ½ больше согласуется с нашим визуальным опытом.

Центральная проекция любой совокупности параллельных прямых, которые не параллельны проекционной плоскости, будет сходиться в точке схода. Точек схода бесконечно много. Если совокупность прямых параллельна одной из главных координатных осей, то их точка схода называется главной точкой схода. Имеются только три такие точки, соответствующие пересечениям главных координатных осей с проекционной плоскостью. Центральные проекции классифицируются в зависимости от числа главных точек схода, которыми они обладают, а следовательно и от числа координатных осей, которые пересекают проекционную плоскость.

1. Одноточечная проекция (рис. 3.13).

 

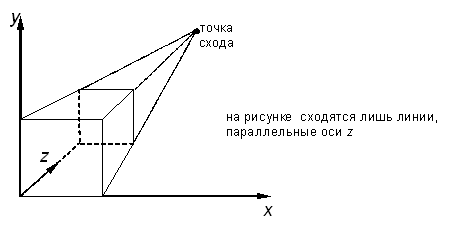
Рис. 3.13. Одноточечная перспектива

2. Двухточечная проекция широко применяется в архитектурном, инженерном и промышленном проектировании.

3. Трехточечные центральные проекции почти совсем не используются, во-первых, потому, что их трудно конструировать, а во-вторых, из-за того, что они добавляют мало нового с точки зрения реалистичности по сравнению с двухточечной проекцией.

 

2) Инвариантные свойства параллельного проецирования

Геометрические фигуры в общем случае проецируются на плоскость проекций с искажением. Проекции не сохраняют линейные и угловые величины оригинала. Характер искажений зависит от положения геометрической фигуры в пространстве, от аппарата проецирования и от положения плоскости проекций.

Однако некоторые геометрические свойства фигур остаются неизменными в процессе проецирования. Такие свойства геометрических фигур называются независимыми или инвариантными для данного аппарата проецирования.

Рассмотрим основные инвариантные свойства параллельного проецирования.

1. Проекция точки есть точка

Это очевидно из самого определения проекции как точка пересечения проецирующей прямой с плоскостью.

2. Проекция прямой есть прямая (рис. 1.6)

.

Рис. 1.6. Инвариантные свойства 2, 3, 4

Все проецирующие прямые, проходящие через точки прямой а параллельно направлению проецирования S, образуют проецирующую, или лучевую, плоскость α.

Проекция прямой а на плоскость π₁ определяется как линия пересечения этой лучевой плоскостиαс плоскостью π₁, т. е. прямая

Если точка К принадлежит прямой а, то и проекция этой точки принадлежит проекции прямой (рис. 1.6).

Это свойство следует непосредственно из определения проекции геометрической фигуры как множества проекций всех точек.

Если точка К принадлежит прямой а и плоскости α, то и проецирующий луч l_К принадлежит плоскости α. Следовательно, этот луч пересечет плоскость π₁ в линии пересечения плоскостей α и π₁, т. е. в точке К₁, принадлежащей проекции прямой а₁.

4. Если точка К делит отрезок АD в отношении m: n то и проекция этой точки делит в таком же отношении проекцию этого отрезка (рис. 1.6):

Фигура ADD₁A₁ – трапеция. Прямая КК₁ параллельна основаниям трапеции АА₁ и DD₁, следовательно делит ее стороны АD и А₁D₁ на пропорциональные части.

5. Проекция точки пересечения прямых есть точка пересечения проекций этих прямых (рис. 1.7)

.

Рис. 1.7. Пример инвариантного свойства 5

Действительно, точка К принадлежит одновременно прямым АВ и CD. По третьему инвариантному свойству проекция этой точки К₁ должна принадлежать проекциям этих прямых, т. е. должна являться точкой пересечения этих проекций.

6. Проекции параллельных прямых параллельны (рис. 1.8)

Лучевые плоскости α и β, проходят через параллельные прямые АВ и CD. Они параллельны, так как две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости (АВ CD и АА₁ СС₁). Но две параллельные плоскости пересекаются с третьей по параллельным прямым, следовательно, А₁В₁ С₁D₁.

7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.

Исключение составляет многоугольник (плоская ломаная или кривая линия) расположенный в проецирующей (лучевой) плоскости. Такой многоугольник проецируется в прямую линию (рис. 1. 9).

.

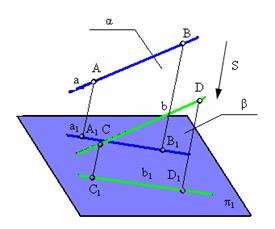Рис. 1.8. Пример инвариантного свойства

.

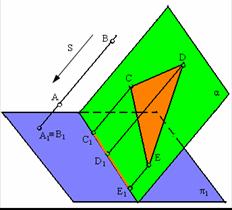
Рис. 1.9. Примеры инвариантных свойств 7, 8

8. Прямая, параллельная направлению проецирования, проецируется в точку (рис. 1.9)

9. Проекция плоской фигуры, параллельной плоскости проекций, конгруэнтна этой фигуре (рис. 1.10).

Следствия этого инвариантного свойства следующие:

1. Проекция отрезка прямой, параллельной плоскости проекций, конгруэнтна и параллельна самому отрезку (рис. 1.10):

2. Проекция угла, стороны которого параллельны плоскости проекций, конгруэнтна этому углу (рис. 1.10).

 

 

Метод Гаспара Монжа

МЕТОД МОНЖА

Если информацию о расстоянии точки относительно плоскости проекции дать не с помощью числовой отметки, а с помощью второй проекции точки, построенной на второй плоскости проекций, то чертеж называют двухкартинным или комплексным. Основные принципы построения таких чертежей изложены Гаспаром Монжем - крупным французским геометром конца 18, начала 19 веков, 1789-1818 гг. одним из основателей знаменитой политехнической школы в Париже и участником работ по введению метрической системы мер и весов.

Постепенно накопившиеся отдельные правила и приемы таких изображений были приведены в систему и развиты в труде Г. Монжа "Geometriedescriptive".

Изложенный Монжем метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций был и остается основным методом составления технических чертежей.

В соответствии с методом предложенным Г. Монжем рассмотрим в пространстве две взаимно перпендикулярные плоскости проекций (рис.6). Одну из плоскостей проекций П ₁ располагают горизонтально, а вторую П ₂ - вертикально. П ₁ - горизонтальная плоскость проекций, П ₂ - фронтальная. Плоскости бесконечны и непрозрачны.

Плоскости проекций делят пространство на четыре двугранных угла – четверти. Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первой четверти на бесконечно большом расстоянии от плоскостей проекций.

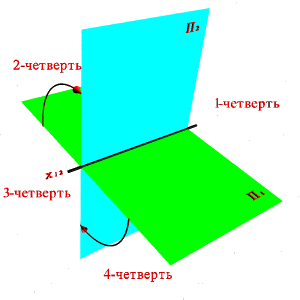
		Линия пересечения плоскостей проекций называется осью координат и обозначается x 12. Так как эти плоскости непрозрачны, то видимыми для наблюдателя будут только те геометрические объекты, которые располагаются в пределах той же первой четверти. Чтобы получить плоский чертеж, состоящий из указанных проекций, плоскость П 1 совмещают вращением вокруг оси x 12 с плоскостью П 2(рис.6).Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещенные определенным образом одна с другой, называется эпюром Монжа (франц. Epure – чертеж.) или комплексным чертежом. Геометрические объекты делятся на: линейные (точка, прямая, плоскость), нелинейные (кривая линия, поверхность) и составные (многогранники, одномерные и двумерные обводы). Рассмотрим способы их образования, графического задания и возможные варианты положения по отношению к плоскостям проекций.
Рисунок 6. Пространственная модель двух плоскостей проекций