Положим (рис.77), требуется определить натуральную величину отрезка,АВ
и угол его с пл. 1. В систему 1, 2 введена пл. 4 % 1 так, что 4
II АВ. Возникла дополнительная система 4, 1. В ней АВ \\ 4 (ось 4/
1 || А'В1); проекция выражает
Натуральную величину отрезка АВ.
ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
Параллельные прямые. К числу свойств параллельного проецирования
относится следующее: проекции двух параллельных прямых параллельны между
собой. Если (рис. 78) прямая АВ параллельна прямой CD, то проецирующие
Плоскости ос и параллельны между собой и при пересечении этих плоскостей с
плоскостью проекций 0 получаются параллельные между собой проекции А°В° и
C°D°.
Однако, хотя А°В° \\ C°D° (рис. 78), прямые, для которых А°В° и
С0D0 являются проекциями, могут быть не параллельны
между собой: например, прямая АВ не параллельна прямой C1D1.
Из указанного свойства параллельного проецирования следует, что
Горизонтальные проекции параллельных прямых параллельны между собой,
Фронтальные проекции параллельны между собой и профильные проекции
Параллельны между собой.
Справедливо ли обратное заключение, т. е. будут ли параллельны две
Прямые в пространстве, если на чертеже их одноименные проекции попарно
параллельны?
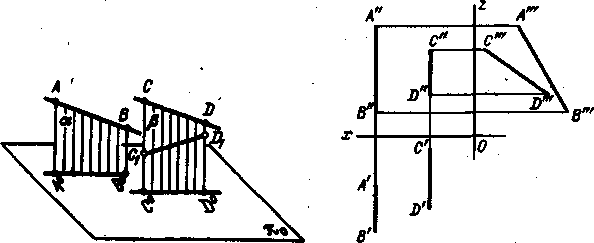

Рис. 78 Рис. 79 Рис. 80
Да, если даны параллельные между собой проекции на каждой из трех
Плоскостей проекций 1, 2 и 3. Но если даны параллельные между собой
Проекции прямых лишь на двух плоскостях проекций, то этим параллельность
Прямых в пространстве подтверждается всегда для прямых общего положения и
Может не подтвердиться для прямых, параллельных одной из плоскостей
Проекций.
Пример дан на рис. 79. Хотя профильные прямые АВ и CD заданы проекциями
А'В', А"В" и CD', C"D", между собой параллельными, но самые прямые не
Параллельны -- это видно из взаимного расположения их профильных проекций,
Построенных по заданным проекциям.
Итак, вопрос был решен при помощи проекций прямых на той плоскости
проекций, по отношению к которой данные! прямые параллельны.
На рис. 80 показан случай, когда можно установить, что профильные
Прямые АВ и CD не параллельны между собой, не прибегая к построению третьей
проекции: достаточно обратить внимание на чередование буквенных
Обозначений.
Если через данную точку А требуется провести прямую, параллельную
данной прямой LM, то (рис. 81, слева) построение сводится к проведению через
точку А" прямой, параллельной L"M", и через точку А' прямой, параллельной
L'M'.

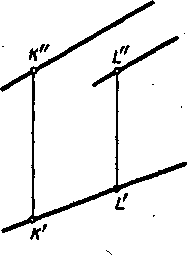
Рис. 81
В случае, изображенном на рис. 81 справа, параллельные прямые






