Положим (рис. 73), что AB есть заданный отрезок (на рис. 71 он
соответствует гипотенузам A'B* и B"A*). Построим на нем, как на диаметре,
Окружность. Приняв точку А за вершину, построим угол (т. е. заданный угол
С пл. 1) и прямоугольный треугольник А1В. Из сравнения этого треугольника с
треугольником А'В'В* (рис. 71) следует, что катет А1 выражает горизонтальную
Проекцию отрезка AB,a катет В1 -- разность расстояний концов отрезка АВ от
Пл. 1.
В. О. Гордон, М. А. Семенцов-Огиевсшй
Построим (рис. 73) также прямоугольный треугольник А2В по той же
гипотенузе AB и заданному углу <рг с плоскостью проекций 2 и сравним его
с треугольником В"А"А* на рис.71. Очевидно, катет В2 выражает· фронтальную
Проекцию заданного отрезка, а катет А2 -- разность расстояний концов отрезка
От пл. 2.
Теперь построим чертеж (рис. 74). Положим, что отрезок надо провести
через точку В влево вниз на себя. Отложив на линии связи B"B' от точки В"
отрезок В"1, равный В! (см. рис. 73), проведем через точку 1 прямую
перпендикулярно к В"В". Засекая эту прямую из точки В" дугой, радиус которой
должен равняться фронтальной проекции, т. е. отрезку В2, получим точку А".
Чтобы найти горизонтальную проекцию А', можно засечь линию связи.

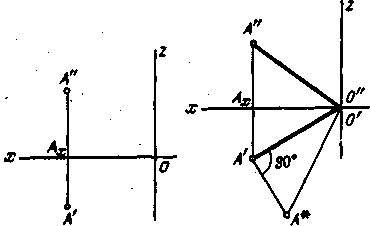
Рис. 73 Рис. 74 Рис. 75
проведенную через точку А", дугой, радиус которой равен А1 (см. рис.
73). При этом должно получиться А"А' -- = А2.
На рис. 74 дано лишь одно положение отрезка. Но может быть еще семь
Других положений при начальной точке В. Предоставляем читателю изобразить
Отрезок АВ и в этих положениях.
На рис. 75 дан пример определения расстояния от точки А до точки О.
Сначала построены проекции искомого отрезка -- А"О" и А'О' (точка О выражена
ее проекциями О" и О'). Затем построен треугольник А'О'А*, один катет
которого -- проекция А'О', другой -- отрезок А'А* = А"АХ. Искомое расстояние
определяется гипотенузой О'А*.
Теперь мы можем определить угол, составляемый прямой, равнонаклоненной
К плоскостям 1, 2 и 3, с этими плоскостями. Об этом угле говорилось в
10, и была указана его величина (~ 35°). Ее можно определить, если
Рассмотреть хотя


Рис. 76 Рис. 77
бы рис. 76: проекции А"В" и А'В' равны между собой, и углы А"В"1 и
2А'В' равны каждый 45° (см. 10).
Искомый угол определен из прямоугольного треугольника А'В'В*, в_котором
катет ' *=. Если принять В"1 равным единице, то А'В' = А"В" = у 2 и угол
-"35°15'. Таковы же углы между этой прямой и плоскостями 2 и 3.
Если применить то, что было сказано в 8, т. е. дополнить систему 1,
2 системой 4, 1, выбрав пл. 4% 1 и параллельно заданному на чертеже
Отрезку прямой линии, то, очевидно, проекция этого отрезка на пл. 4 выразит






