Прямая линия, получаемая при взаимном пересечении двух плоскостей,
Вполне определяется двумя точками, из которых каждая принадлежит обеим
плоскостям. Так, прямая К1К2 (рис. 163), по которой пересекаются между собой
Плоскость, заданная треугольником ABC, и пл., заданная прямыми DE и DF,
Проходит через точки и К2, но в этих точках

Прямые АВ и АС первой плоскости пересекают пл., т.е. точки К и Кг
Принадлежат, обеим плоскостям.
Следовательно, в общем случае для построения линии пересечения двух
Плоскостей надо найти какие-либо две точки, комедия из которых принадлежит
Обеим плоскостям; эти точки определяют линию пересечения плоскостей.
Для нахождения каждой из таких двух точек обычно приходится выполнять
Специальные построения. Но если хотя бы одна из пересекающихся плоскостей
Перпендикулярна к плоскости проекций, то построение проекций линии
Пересечения упрощается. Начнем с такого случая.
На рис. 164 показано пересечение двух плоскостей, из которых одна
(заданная треугольником DEF) расположена перпендикулярно к пл. п2. Так как
треуголь-шк,ОЕР проецируется на пл. 2 в виде прямой линии (D"F"), то
Фронтальная проекция отрезка прямой, по которому пересекаются оба
треугольника, представляет собой отрезок К'[К'2 на проекции D"F". Дальнейшее
Построение ясно из чертежа.

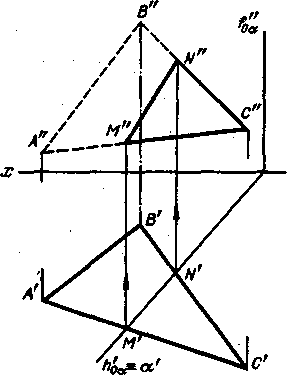
Рис. 165
Другой пример дан на рис. 165. Горизонтально-проецирующая плоскость
Пересекает плоскость треугольника ABC. Горизонтальная проекция линии
пересечения этих плоскостей -- отрезок M'N' -- определяется на следе '.
Теперь рассмотрим общий случай построения линии пересечения двух
Плоскостей. Пусть одна из плоскостей,, задана двумя пересекающимися
Прямыми, а другая,,-- двумя параллельными прямыми. Построение показано на
рис. 166. В результате взаимного пересечения плоскостей и получена
прямая К1К2. Выразим это записью: · = 1 2·
Для определения положения точек К1 и К2 возьмем две вспомогательные
Фронтально-проецирующие плоскости (1, и 2), пересекающие каждую из
Плоскостей и. При пересечении плоскостей и плоскостью 1 получаем
прямые с проекциями 1"2", 1'2' и 3"4", 3'4'. Эти прямые, расположенные в пл.
В своем пересечении определяют первую точку, К1, линии пересечения
Плоскостей и.
Введя, далее, пл. 2, получаем в ее пересечении с и прямые с
проекциями 5"б", 5'6' и 7"8", 7'8'. Эти прямые, расположенные в пл. а2, в
Своем пересечении определяют вторую точку, К2, общую для и.
Получив проекции К1' и К'2, находим на следах
"1 и "2 проекции К"1 и К "2.
Этим определяются проекции К'1К '2 и К"1К"2






