Прямая линия может занимать относительно плоскостей проекций особые (иначе, частные) положения. Рассмотрим их по следующим двум признакам:
А. Прямая параллельна одной плоскости проекций.
Б. Прямая параллельна двум плоскостям проекций.
В первом случае одна проекция отрезка прямой равна самому отрезку. Во втором случае две проекции отрезка равны ему1).
А. Прямая параллельна одной плоскости проекций
1. Прямая параллельна пл., (рис. 50). В таком случае фронтальная проекция прямой параллельна оси проекций и горизонтальная проекция отрезка этой прямой равна самому отрезку: А'В'=АВ. Такая прямая называется горизонтальной.
Если, например, проекция А"В" совпадает с осью проекций, то отрезок АВ расположен в пл., 2).



Рис. 50
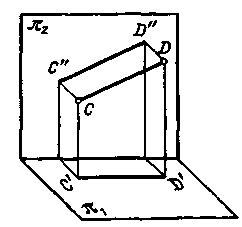

Рис. 51
2. Прямая параллельна пл. 2 (рис. 51). В таком случае ее горизонтальная проекция параллельна оси проекций и фронтальная проекция отрезка этой прямой равна самому отрезку: C"D" = CD. Такая прямая называется фронтальной.
Если, например, проекция C'D' совпадает с осью проекций, то это соответствует положению отрезка CD в самой пл. 2.
') Все это, конечно, с учетом масштаба чертежа.
2) На рис. 50 справа дан чертеж без указания оси проекций. То же сделано на рис. 51.
3. Прямая параллельна пл. 3 (рис. 52). В таком случае горизонтальная и фронтальная проекции прямой располагаются на одном перпендикуляре к оси проекций Ох и профильная проекция этой прямой равна самому отрезку: E"F" = EF. Такая прямая называется профильной.



Рис. 52 Рис. 53
Можно ли считать, что на чертежах, подобных указанным на рис. 50 и 51, изображены отрезки именно прямых линий? Да; доказательство такое же, как для прямой общего положения (рис. 46).
Если же на чертеже в системе 5 2 обе проекции перпендикулярны к оси проекций, то проецирующие плоскости, проведенные через E'F и E"F", сливаются в одну и оригиналом может быть не только прямая линия, но и некоторая плоская кривая (рис. 53).
Б. Прямая параллельна двум плоскостям проекций
1. Прямая параллельна плоскостям 1 и 2 (рис. 54), т. е. перпендикулярна к пл. 3. Проекция на пл. 3 представит собой точку.
2. Прямая параллельна плоскостям, и 3 (рис. 55), т. е. перпендикулярна к пл. 2. Проекция на пл. 3 представляет собой отрезок прямой, равный CD'.

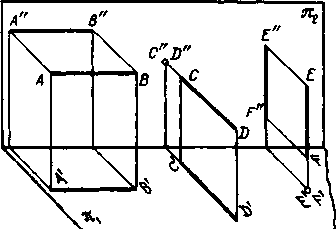
Рис. 54 Рис. 55 Рис. 56 Рис. 57
3. Прямая параллельна плоскостям 2 и 3 (рис. 56), т. е. перпендикулярна к
пл. nt. Проекция на пл. 3 представит собой отрезок, параллельный и равный E"F".
На рис. 57 дано наглядное изображение положения рассмотренных прямых').
') Для этих прямых встречается название "проецирующие прямые".

Рис. 58 Рис. 59
Обычно строятся проекции отрезков прямой линии с указанием концевых точек отрезка. Если же по каким-либо причинам показывают некоторую неопределенную часть прямой линии, то практически тоже показывают отрезок линии, но не обозначают концевых точек этого отрезка. При этом можно пользоваться обозначением каждой проекции только одной буквой, относя ее к какой-либо точке прямой (рис. 58): "прямая, проходящая через точку А".
Обратим внимание на чертеж слева на рис. 59. Относительно прямой, изображенной на нем, можно сказать лишь то, что она проходит через точку L и параллельна пл. jtj, но в остальном положение этой прямой не определяется. Определенность была бы внесена горизонтальной проекцией, т. е. проекцией на плоскости, по отношению к которой прямая параллельна.
Если же мы имеем дело с прямой, заданной двумя своими точками (например, с отрезком прямой, заданным своими концами), то можно точно определить положение этой прямой и в том случае, если не задана ее проекция на плоскости, параллельной этой прямой. Так, например, если дан отрезок АВ прямой (рис. 59, справа), то мы можем установить не только параллельность этой прямой по отношению к пл. -, но и то, что точка A данной прямой более удалена от пл. 2, чем точка В.
8) Точка на прямой
Комплексный чертеж точки, находящейся на прямой. Точку на прямой можно рассматривать как одну из точек, принадлежащих этой прямой. Пусть дан отрезок АВ и его проекции А1В1 и А2В2. На отрезке АВ лежит точка С, требуется определить ее проекции. Так как точка принадлежит отрезку, то ее проекции будут лежать на одноименных проекциях отрезка (фиг.211,а).
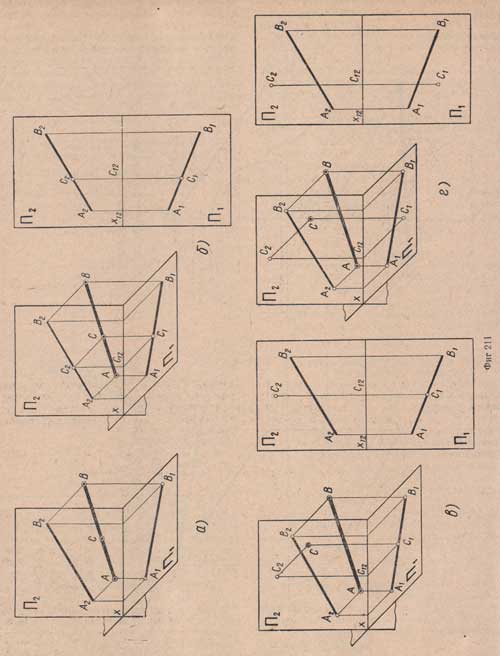
Проведем через точку С проектирующие прямые, получим горизонтальную проекцию С1 точки С на горизонтальной проекции А1В1 отрезка АВ и фронтальную проекцию С2 на фронтальной проекции А2В2 (фиг.211,б). Рассматривая комплексный чертеж точки С, замечаем, что обе проекции С1 и С2 лежат на одной вертикальной линии связи, как проекции одной и той же точки. Если одна (фиг.211,в) или две проекции (фиг.211,г) точки не лежат на одноименных проекциях отрезка, то точка не лежит на отрезке.
Следовательно, для того чтобы точка лежала на прямой, необходимо, чтобы проекции этой точки не только лежали на одноименных проекциях прямой, но и находились на одной линии связи.
Это правило имеет исключение в том случае, когда точка лежит на горизонтальной прямой, данной фронтальной и профильной проекциями, на фронтальной прямой, данной горизонтальной и профильной проекциями, или профильной прямой, данной горизонтальной и фронтальной проекциями.

Тогда, для того чтобы определить, лежит ли точка на прямой, необходимо построить третью проекцию. На (фиг.212) видно, что точка Е не лежит на отрезке АВ, так как профильная проекция Е3 точки Е не лежит на профильной проекции А3В3 отрезка АВ; точка F лежит на отрезке АВ, так как не только ее горизонтальная F1 фронтальная F2, но и профильная F3 проекции лежат на одноименных проекциях отрезка АВ.
9) Следы прямой
Следом прямой называется, точка пересечения прямой с плоскостью проекций. Точка пересечения прямой с плоскостью П1 называется горизонтальным следом прямой и обозначается буквой М; точка пересечения прямой с плоскостью П2 - фронтальным cледом и обозначается буквой N (фиг.216).

Следы прямой являются точками, одновременно принадлежащими как плоскости проекций, так и прямой.
Фронтальная проекция фронтального следа и горизонтальная проекция горизонтального следа будут лежать в плоскостях проекций и совпадать с самим следом. Фронтальная проекция горизонтального следа и горизонтальная проекция фронтального следа будут лежать на оси проекций. Прямая, расположенная параллельно плоскости проекций, как находящаяся на всем своем протяжении на одинаковом расстоянии от плоскости, следа на ней не имеет. Разберем на комплексном чертеже порядок нахождения следов отрезка прямой АВ общего положения (фиг.217).
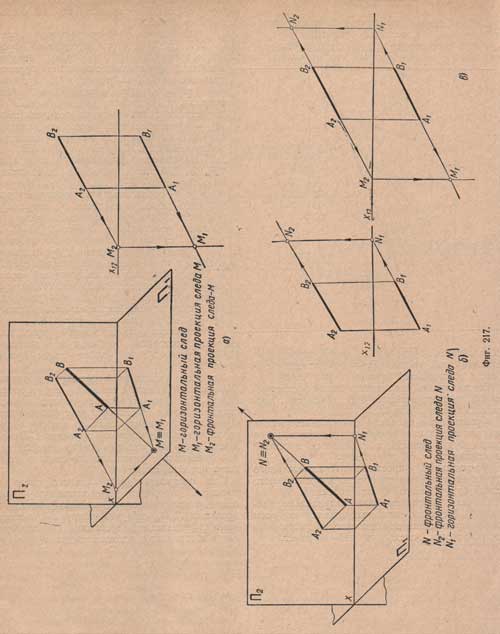
1. Нахождение горизонтального следа (фиг.217,a). Для этого продолжим фронтальную проекцию A2В2 До оси х12, получим в точке М2 фронтальную проекцию горизонтального следа; из точки М2 проводим вниз вертикальную линию связи, затем продолжим горизонтальную проекцию А1В1 до встречи с линией связи, получим точку М1 - горизонтальную проекцию горизонтального следа и в то же время сам горизонтальный след М данного отрезка АВ.
2. Нахождение фронтального следа (фиг.217,б). Для этого продолжим горизонтальную проекцию А1В1 до оси х12, получим в точке N1 горизонтальную проекцию фронтального следа, и из точки N1 вверх проводим вертикальную линию связи, затем продолжим фронтальную проекцию А2В2 до встречи с линией связи, получим точку N2 - фронтальную проекцию фронтального следа и в то же время фронтальный след N. В результате получим комплексный чертеж следов отрезка прямой АВ (фиг.217,в).
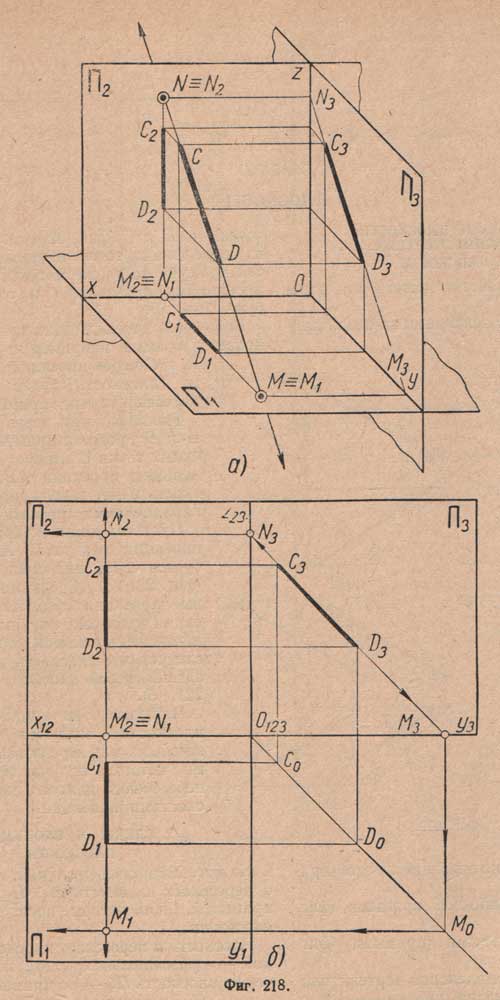
Это построение имеет исключение в случае, когда прямая параллельна, например, профильной плоскости П3 (фиг. 218,а).