ОТРЕЗКА ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ
И УГЛОВ НАКЛОНА ПРЯМОЙ К ПЛОСКОСТЯМ ПРОЕКЦИЙ 1 и 2
Из рассмотрения левой части рис. 69 можно заключить, что отрезок АВ
Является гипотенузой прямоугольного треугольника АВ1, в котором один катет
равен проекции отрезка (А1 = А°В°), а другой катет равен разности расстояний
Концов отрезка от плоскости проекций 0.

Рис. 69
Если координаты, определяющие расстояния концов отрезка от плоскости
проекций, имеют разные знаки (рис. 69, справа), то надо иметь в виду
разность алгебраическую:
В1 = ВВ° - (-АА0) = ВВ° + АА°.
Угол прямой линии с плоскостью проекций определяется как угол,
Составленный прямой с ее проекцией на этой плоскости. Этот _ угол входит в
Тот же прямоугольный треугольник, который строят для определения натуральной
Величины отрезка.
Очевидно, зная по чертежу катеты треугольника, можно его построить в
любом месте поля чертежа. На рис. 70 показано построение, примененное Г.
Монжем:
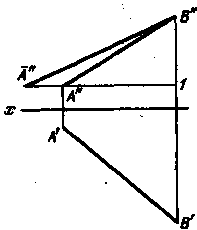

Рис. 70 Рис. 71 Рис. 72
от точки 1 отложен отрезок, равный проекции A'ff, и проведена
гипотенуза А"У, выражающая натуральную величину отрезка АВ. Угол с вершиной
в точке А" равен углу между АВ и пл. 1
На рис. 71 слева длина отрезка АВ и угол, составленный прямой АВ с пл.
1определены из прямоугольного треугольника, построенного на проекции А'В'
при втором катете В'В*, равном В"1. АВ = А'В*.
На рис. 71 справа длина отрезка и угол, составленный с пл. п2,
определены из прямоугольного треугольника, построенного на проекции А"В"
(А"А* = А'2). АВ = В"А*.
Ограничены ли чем-либо углы. и - для прямой общего положения? Да,
Каждый из них может быть только острым. Но, кроме того, для прямой общего
положения - + - < 90°. Действительно (рис. 72), в прямоугольном
треугольнике " " ' сумма углов + - = 90°. Но в треугольниках " " '
' ' ' при общей гипотенузе " ' катет " " больше катета " ' и,
следовательно, > 1. Подставляя в + 2=90° угол вместо, получим
1+ 2<90°.
Рассмотрим (рис. 71) прямоугольные треугольники А'В'В* и A"B"A*. В
Каждом из них гипотенуза выражает натуральную величину отрезка, а один из
Катетов является проекцией этого отрезка. Другой же катет равен разности
расстояний концов отрезка от соответствующей плоскости проекций (В'В* - В"1
= разности расстояний от nlt a A"A* = А'2 = разности расстояний от я2).
Кроме того, в одном из этих треугольников содержится угол между отрезком и
Пл. 1 (угол), в другом -- угол между отрезком и пл. 2 (угол 2).
В данном случае нам были известны катеты и мы определяли гипотенузу и
угол. Но может быть и такое положение: известны гипотенуза и угол,
Определить катеты (т. е. даны натуральная величина отрезка и углы,






