Решение:
По определению коэффициента корреляции 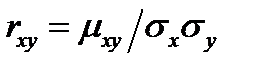 , где
, где
 (*)
(*)
Найдем математическое ожидание 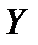 :
:
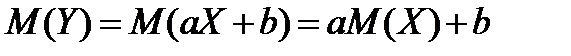 (**)
(**)
Подставив (**) в (*), после элементарных преобразований получим
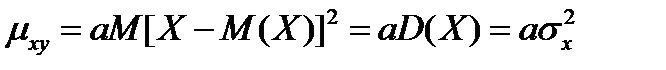 .
.
Учитывая, что
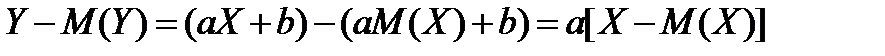 , найдем дисперсию
, найдем дисперсию 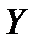 :
:
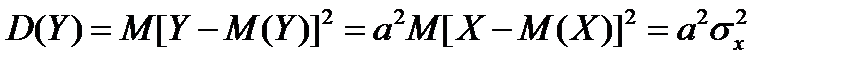 .
.
Отсюда 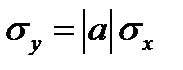 .Следовательно, коэффициент корреляции
.Следовательно, коэффициент корреляции
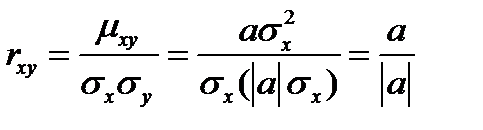 .
.
Если 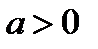 , то
, то 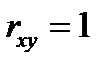 ; если
; если 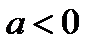 , то
, то 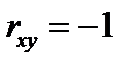 .
.
Итак, 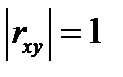 , что и требовалось доказать.
, что и требовалось доказать.
№439 Выборка задана в виде распределения частот:
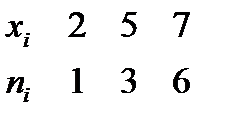
Найти распределение относительных частот.
Решение:
Найдем объем выборки; 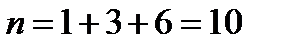 . Найдем
. Найдем
относительные частоты:
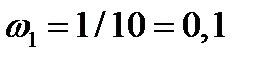 ;
;  ;
; 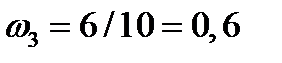 .
.
Напишем искомое распределение относительных частот:
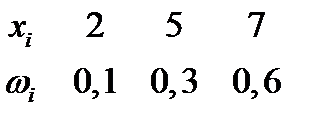
Контроль:  .
.
№440 Выборка задана в виде распределения частот:
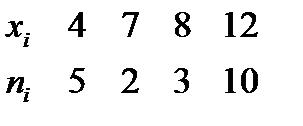
Найти распределение относительных частот.
Решение:
Найдем объем выборки: 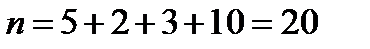 . Найдем
. Найдем
относительные частоты:
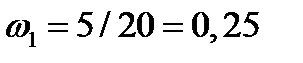 ;
; 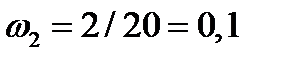 ;
; 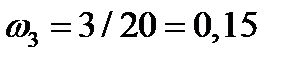 ;
; 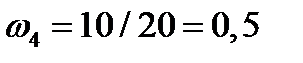 .
.
Напишем искомое распределение относительных частот:

Контроль: 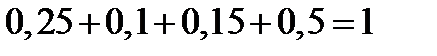 .
.
№441 Найти эмпирическую функцию по данному распределению выборки:
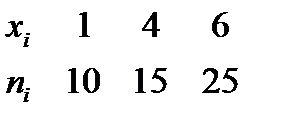
Решение:
Найдем объем выборки: 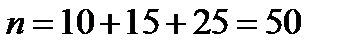 .
.
Наименьшая варианта равна единице, поэтому 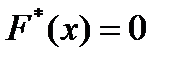 при
при
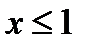 .
.
Значение  , а именно
, а именно 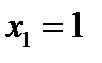 , наблюдалось 10 раз, следовательно,
, наблюдалось 10 раз, следовательно,
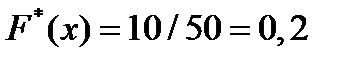 при
при 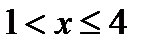 .
.
Значения 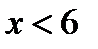 , а именно:
, а именно:  и
и 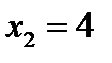 , наблюдались 10+12=25 раз; следовательно,
, наблюдались 10+12=25 раз; следовательно, 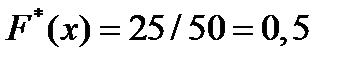 при
при  .
.
Так как 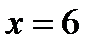 — наибольшая варианта, то
— наибольшая варианта, то 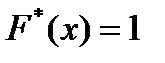 при
при  .
.
Напишем искомую эмпирическую функцию:
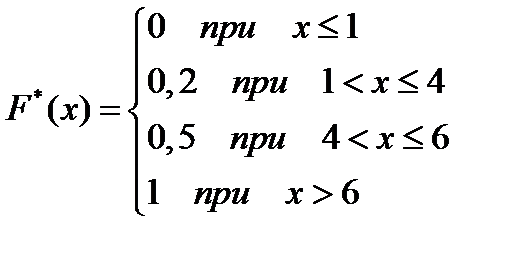
№442 Найти эмпирическую функцию по данному распределению выборки:
а) 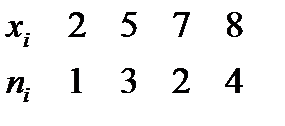
б) 
Решение:
а) Найдем объем выборки: 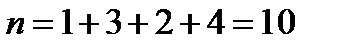 .
.
Наименьшая варианта равна 2, поэтому 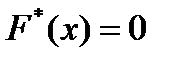 при
при 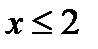 .
.
Значение 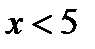 , а именно
, а именно 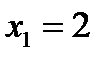 , наблюдалось 1 раз, следовательно,
, наблюдалось 1 раз, следовательно,
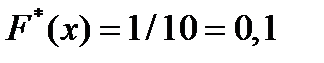 при
при 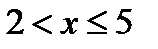 .
.
Значения 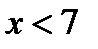 , а именно:
, а именно: 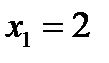 и
и  , наблюдались
, наблюдались 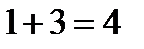 раз; следовательно,
раз; следовательно, 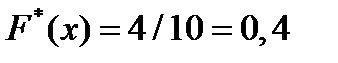 при
при 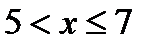 .
.
Значения 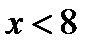 , а именно:
, а именно: 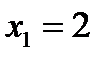 ,
, 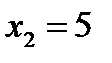 ,
, 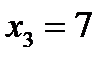 , наблюдались
, наблюдались 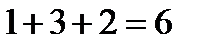 раз; следовательно,
раз; следовательно, 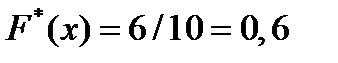 при
при 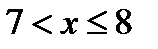 .
.
Так как 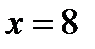 — наибольшая варианта, то
— наибольшая варианта, то  при
при 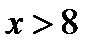 .
.
Ответ: 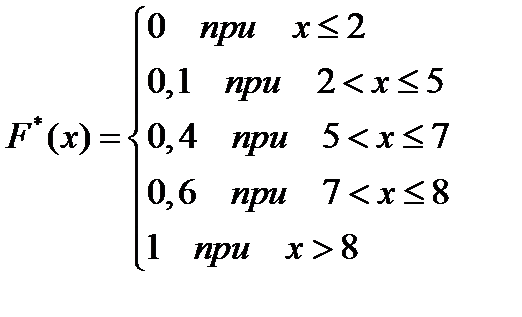
б) Найдем объем выборки:  .
.
Наименьшая варианта равна 4, поэтому 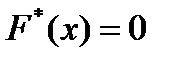 при
при  .
.
Значение 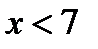 , а именно
, а именно 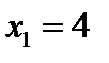 , наблюдалось 5 раз, следовательно,
, наблюдалось 5 раз, следовательно,
 при
при 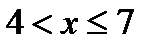 .
.
Значения 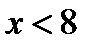 , а именно:
, а именно: 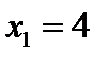 и
и 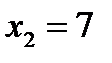 , наблюдались
, наблюдались 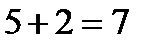 раз; следовательно,
раз; следовательно, 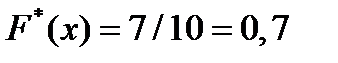 при
при 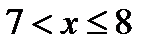 .
.
Так как 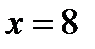 — наибольшая варианта, то
— наибольшая варианта, то 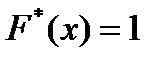 при
при 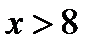 .
.
Ответ: 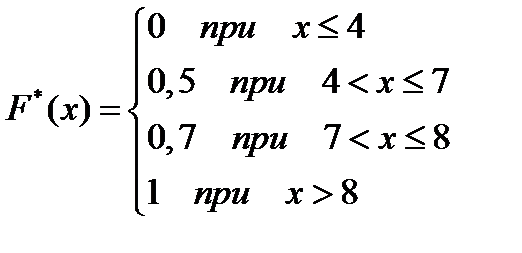
№443 Построить полигон частот по данному распределению выборки:
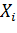
| 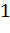
| 
| 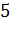
| 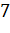
|
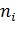
| 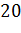
| 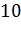
| 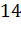
| 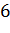
|
Решение.
Отложим на оси абсцисс варианты 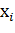 , а на оси ординат —соответствующие им частоты
, а на оси ординат —соответствующие им частоты 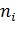 соединив точки
соединив точки 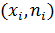 отрезками прямых, получим искомый полигон частот.
отрезками прямых, получим искомый полигон частот.
№444 Построить полигон частот по данному распределению выборки:
а)
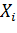
| 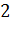
| 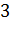
| 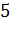
| 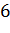
|
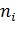
| 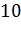
| 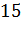
| 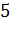
| 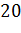
|



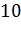
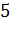
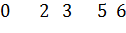
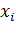
б)
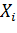
| 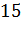
| 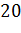
| 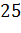
| 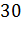
| 
|
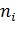
| 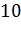
| 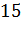
| 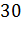
| 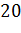
| 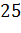
|



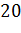
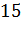
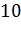
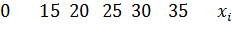
№445 Построить полигон относительных частот по данному распределению выборки:
А).
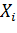
| 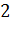
| 
| 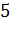
| 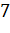
| 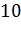
|
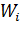
| 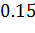
| 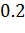
| 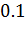
| 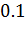
| 
|
Решение:
Отложим на оси абсцисс варианты 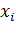 а на оси
а на оси
ординат—соответствующие относительные частоты 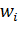 . Соединив точки
. Соединив точки
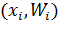 отрезками прямых, получим искомый полигон относительных частот
отрезками прямых, получим искомый полигон относительных частот
Б).
| 
| 
| 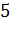
| 
| 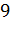
|
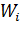
| 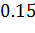
| 
| 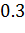
| 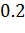
| 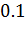
|

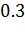


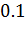
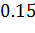
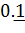
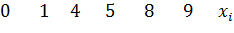
В).
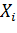
| 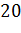
| 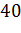
| 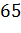
| 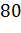
|
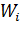
| 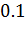
| 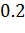
| 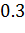
| 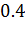
|



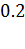
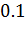
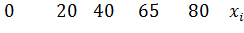
№446 Построить гистограмму частот по данному распределению выборки объема n=100:

| 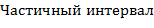
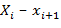
| 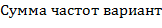
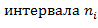
| 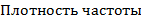
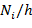
|
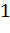
| 
| 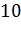
| 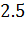
|
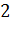
| 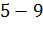
| 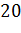
| 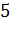
|
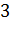
| 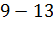
| 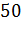
| 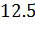
|

| 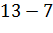
| 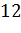
| 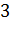
|
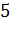
| 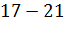
| 
| 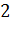
|
Решение.
Построим на оси абсцисс заданные интервалы длины
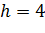 . Проведем над этими интервалами отрезки, параллельные оси
. Проведем над этими интервалами отрезки, параллельные оси
абсцисс и находящиеся от нее на расстояниях, равных соответствующим
плотностям частоты 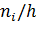 . Например, над интервалом
. Например, над интервалом 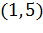
построим отрезок, параллельный оси абсцисс, на расстоянии 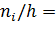
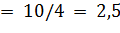 ; аналогично строят остальные отрезки.
; аналогично строят остальные отрезки.
№447 Построить гистограмму частот по данному распределению выборки:

| 
| 

| 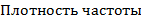
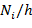
|
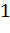
| 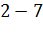
| 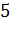
| 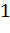
|
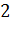
| 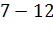
| 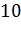
| 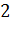
|
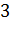
| 
| 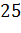
| 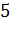
|

| 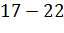
| 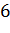
| 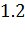
|
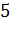
| 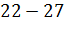
| 
| 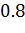
|




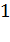
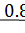
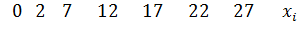

| 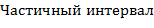
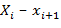
| 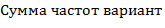

| 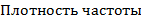
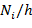
|
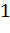
| 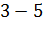
| 
| 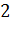
|
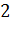
| 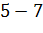
| 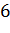
| 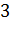
|
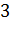
| 
| 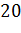
| 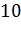
|

| 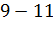
| 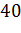
| 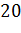
|
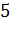
| 
| 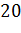
| 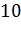
|
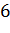
| 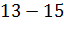
| 
| 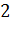
|
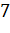
| 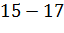
| 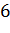
| 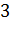
|




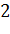

№448 Построить гистограмму относительных частот по данному распределению выборки:

| 
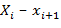
| 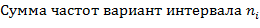
|
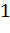
| 
| 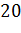
|
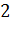
| 
| 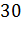
|
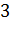
| 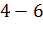
| 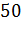
|
Решение. Найдем относительные частоты:
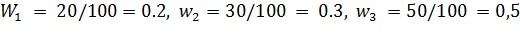 .
.
Найдем плотности относительных частот, учитывая, что длина
интервала h=2:
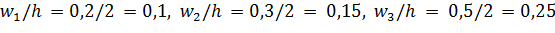 .
.
Построим на оси абсцисс данные частичные интервалы. Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от нее на расстояниях, равных соответствующим плотностям относительной частоты. Например, над интервалом (О, 2) проведем отрезок, параллельный оси абсцисс и находящийся от нее на расстоянии, равном 0,1; аналогично строят остальные отрезки.
№449 Построить гистограмму относительных частот по данному распределению выборки:
а)

| 
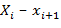
| 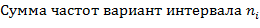
|
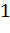
| 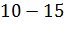
| 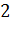
|
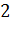
| 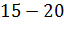
| 
|
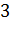
| 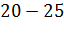
| 
|

| 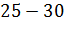
| 
|
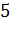
| 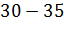
| 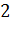
|
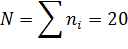
Решение. Найдем относительные частоты:
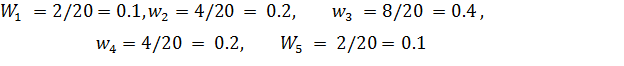
Найдем плотности относительных частот, учитывая, что длина
интервала h=5:
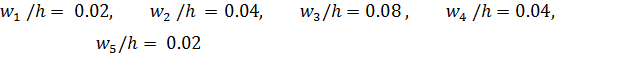
Построим на оси абсцисс данные частичные интервалы. Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от нее на расстояниях, равных соответствующим плотностям относительной частоты.
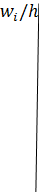


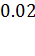
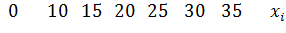

| 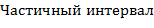
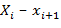
| 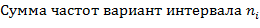
|
| 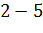
| 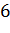
|
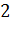
| 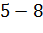
| 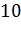
|
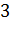
| 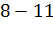
| 
|

| 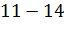
| 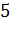
|
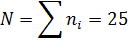
Решение.
Найдем относительные частоты:

Найдем плотности относительных частот, учитывая, что длина
интервала h=3:
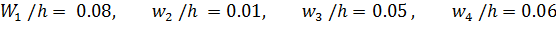
Построим на оси абсцисс данные частичные интервалы. Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от нее на расстояниях, равных соответствующим плотностям относительной частоты.
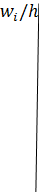



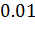
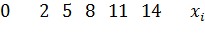
№450 Из генеральной совокупности извлечена выборка объема n = 50:
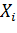
| 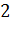
| 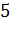
| 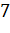
| 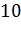
|
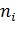
| 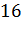
| 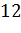
| 
| 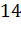
|
Найти несмещенную оценку генеральной средней.
Решение. Несмещенной оценкой генеральной средней является выборочная средняя
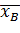 = (
= (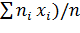
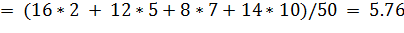 .
.
№451 Из генеральной совокупности извлечена выборка объема n=60:
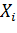
| 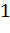
| 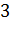
| 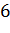
| 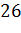
|
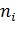
| 
| 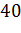
| 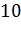
| 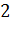
|
Хi 1 3 6 26
ni 8 40 10 2
Найти несмещенную оценку генеральной средней.
Решение.
Несмещенной оценкой генеральной средней является выборочная средняя
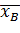 = (
= (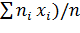 =
= 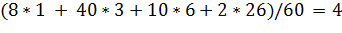 .
.
№452 Задано распределение первоначальных вариант выборки объема п:
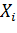
| 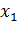
| 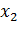
| 
| 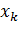
|
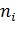
| 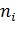
| 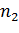
| 
| 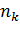
|
Доказать, что
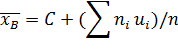
где условные варианты 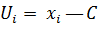
Решение. Так как 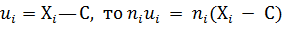 ; суммируя
; суммируя
левую и правую части равенства по всем значениям i получим
 =
= 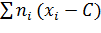 или
или  =
= 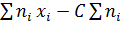 =
= 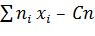
Отсюда
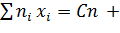

Следовательно,
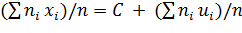 или
или
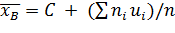 , что и требовалось доказать.
, что и требовалось доказать.
№453 Найти выборочную среднюю по данному распределению выборки объема n=10:
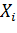
| 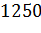
| 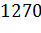
| 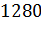
|
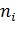
| 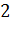
| 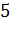
| 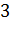
|
Решение. Первоначальные варианты — большие числа, поэтому
перейдем к условным вариантам. 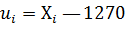 . В итоге получим
. В итоге получим
распределение условных вариант:
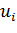
| 
| 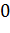
| 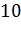
|
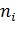
| 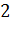
| 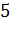
| 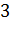
|
Найдем искомую выборочную среднюю:
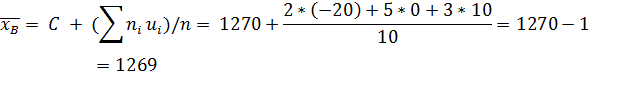
Саградов Арсен
№454 Найти выборочную среднюю по данному распределению выборки объема n=20:
| xi | |||||
| ni |
Решение:
Первоначальные варианты – большие числа, поэтому перейдем к условным вариантам ui=xi – 2620. В итоге получим распределение условных вариант
| ui | -60 | -20 | |||
| ni |
Найдем искомую выборочную среднюю
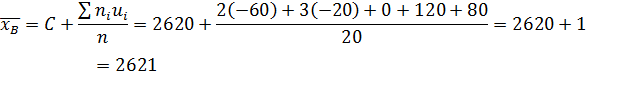
Ответ: 2621
№455. По выборке объема n = 41 найдена смещенная оценка 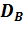 = 3 генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.
= 3 генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.
Решение.
Искомая несмещенная оценка равна исправленной
дисперсии:
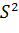 =
= 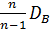 =
= 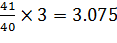
№456 По выборке объема n=51 найдена смещенная оценка DB=5 генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.
Решение
Искомая несмещенная оценка равна исправленной дисперсии
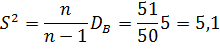
Ответ 5,1
№457. В итоге пяти измерений длины стержня одним прибором (без систематических ошибок) получены следующие результаты (в мм): 92; 94; 103; 105; 106. Найти: а) выборочную среднюю длину стержня; б) выборочную
и исправленную дисперсии ошибок прибора.
Решение:
а) Найдем выборочную среднюю:
 = 92 +(0+2 + 11 + 13 + 14)/5=92+8 =100.
= 92 +(0+2 + 11 + 13 + 14)/5=92+8 =100.
б) Найдем выборочную дисперсию:
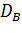 =
= 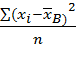 =[
=[ 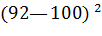 +
+ 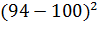 +
+ 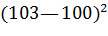 ]/5+
]/5+
+ 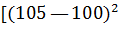 +
+ 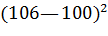 ]/5 = 34.
]/5 = 34.
Найдем исправленную дисперсию:
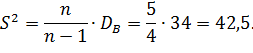
№458 В итоге 4 измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты: 8; 9; 11; 12. Найти: А) Выборочную среднюю результатов измерений; Б) Выборочную и исправленную дисперсии ошибок прибора.
Решение
А) Найдем выборочную среднюю
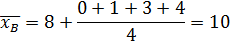
Б) Найдем выборочную дисперсию
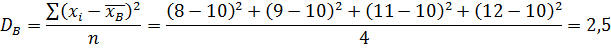
Найдем исправленную дисперсию
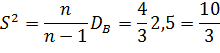
Ответ: 10; 2,5; 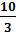
№459 Ниже приведены результаты измерения роста (в см) случайно отобранных 100 студентов
| Рост | 154-158 | 158-162 | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 |
| Число студентов |
Найти выборочную среднюю и выборочную дисперсию роста обследованных студентов
Решение
Найдем середины интервалов и примем их в качества вариант
Найдем выборочную среднюю

Найдем выборочную дисперсию
Перейдем к условным вариантам ui=xi – 168. В итоге получим распределение условных вариант
| ui | -12 | -8 | -4 | ||||
| ni |
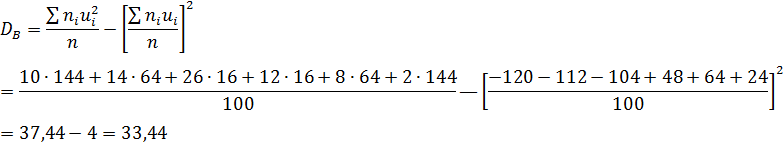
Ответ: 166; 33,44
№460. Найти выборочную дисперсию по данному распределению
выборки объема n=10:
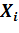 186 192 194
186 192 194
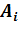 2 5 3
2 5 3
Решение.
Варианты—сравнительно большие числа, поэтому
перейдем к условным вариантам 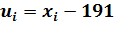 (мы вычли из вариант
(мы вычли из вариант
число С = 191, близкое к выборочной средней). В итоге получим
распределение условных вариант:
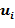 —5 1 3
—5 1 3
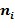 2 5 3
2 5 3
Найдем искомую выборочную дисперсию:
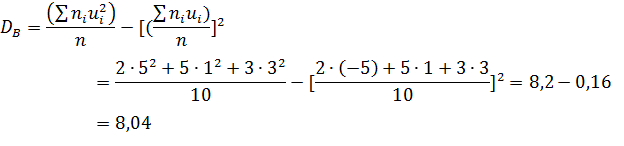
№461 Найти выборочную дисперсию по данному распределению выборки объема n=100
| xi | ||||
| ni |
Решение
Перейдем к условным вариантам ui=xi – 360. В итоге получим распределение условных вариант
| ui | -20 | |||
| ni |
Найдем искомую выборочную дисперсию
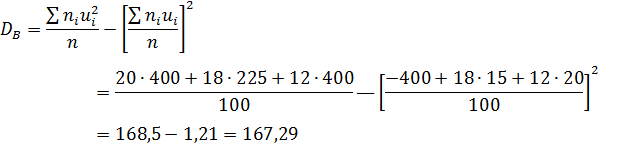
Ответ: 167,29
№462 Найти выборочную дисперсию по данному распределению выборки объема n=100
| xi | ||||
| ni |
Решение
Перейдем к условным вариантам ui=xi – 2844. В итоге получим распределение условных вариант
| ui | -342 | -40 | ||
| ni |
Найдем искомую выборочную дисперсию

Ответ: 12603
№463. Найти выборочную дисперсию по данному распределению
выборки объема n=10:
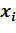 0,01 0,04 0,08
0,01 0,04 0,08
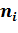 5 3 2
5 3 2
Решение.
Для того чтобы избежать действий с дробями,
перейдем к условным вариантам 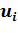 =100
=100 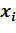 . В итоге получим распределение
. В итоге получим распределение
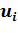 1 4 8
1 4 8
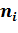 5 3 2
5 3 2
Найдем выборочную дисперсию условных вариант:
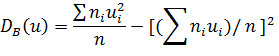
Подставив в эту формулу условные варианты и их частоты, получим
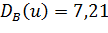
Найдем искомую выборочную дисперсию первоначальных вариант:
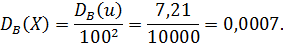
№464 Найти выборочную дисперсию по данному распределению выборки объема n=50
| xi | 0,1 | 0,5 | 0,6 | 0,8 |
| ni |
Решение
Перейдем к условным вариантам ui=10xi. В итоге получим распределение условных вариант
| ui | ||||
| ni |
Найдем искомую выборочную дисперсию
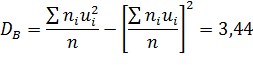
Найдем искомую выборочную дисперсию первоначальных вариант
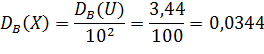
Ответ: 0,0344
№465 Найти выборочную дисперсию по данному распределению выборки объема n=50
| xi | 18,4 | 18,9 | 19,3 | 19,6 |
| ni |
Решение
Перейдем к условным вариантам ui=10xi -195. В итоге получим распределение условных вариант
| ui | -11 | -6 | -2 | |
| ni |
Найдем искомую выборочную дисперсию
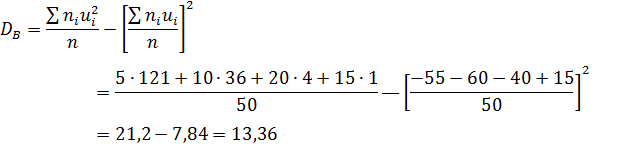
Найдем искомую выборочную дисперсию первоначальных вариант

Ответ: 0,1336
№466. Найти исправленную выборочную дисперсию по данному распределению выборки n =10:
| xi | |||
| ni |
Решение.
Перейдем к условным вариантам ui = xi —104.
В итоге получим распределение
| ui | -2 | ||
| ni |
Найдем исправленную выборочную дисперсию условных вариант:
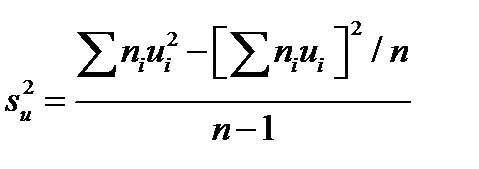
Подставив в эту формулу условные варианты, их частоты и объем выборки, получим 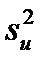 =6,93.
=6,93.
Все первоначальные варианты были уменьшены на одно и то же постоянное число С=104, поэтому дисперсия не изменилась, т. е. искомая дисперсия равна дисперсии условных вариант: 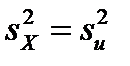 =6,93.
=6,93.
№467. Найти исправленную выборочную дисперсию по данному распределению выборки объема n = 100:
| xi | ||||
| ni |
Указание. Перейти к условным вариантам ui=xi —1275.
Решение.
Перейдем к условным вариантам ui=xi —1275.
В итоге получим распределение
| ui | -25 | |||
| ni |
Воспользуемся формулой






