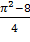где 
—функция, обратная функции y=4tg t
Найдем
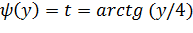
Найдем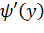 
:
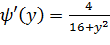y
Следовательно,
(**)
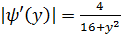Найдем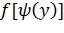 
. Так как 
.
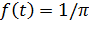то
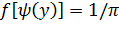(***) y A(4;0)
Подставив (**) и (***) в (*), окончательно рис. 1 x
получим,
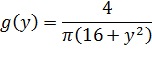
причем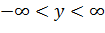 
(последнее следует из того, что y=4tg t и 
)
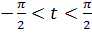Контроль:
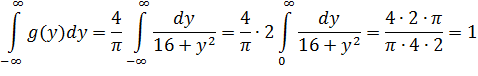
№ 383. Случайная величина X равномерно распределена в интервале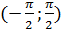 
. Найти плотность распределения g(y) случайной величины Y =sinX.
Решение:
Найдем плотность распределения f(х) случайной величины X. Величина X распределена равномерно в интервале 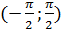, поэтому в этом интервале
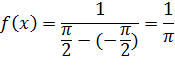
вне рассматриваемого интервала f(x)=0.
Функция y=sin x в интервале 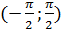монотонна, следовательно,
в этом интервале она имеет обратную функцию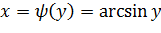 
.
Найдем производную :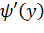
Найдем искомую плотность распределения по формуле:
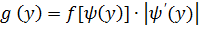
Учитывая, что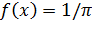 
(следовательно, 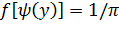) и
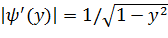, получим
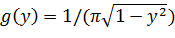
Так как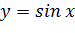 
, причем 
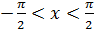, то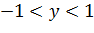 
. Таким образом, в интервале (
1,1) имеем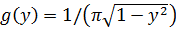 
;вне этого интервала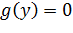 
Контроль:
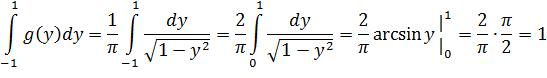
Лукинова Наталья
№384 Случайная величина X распределена равномерно в интервале (0; 
). Найти плотность распределения g(y) случайной величины Y=sin X.
Решение:
Найдем плотность распределения f(x) случайной величины X. Величина X распределена равномерно в интервале (0; ), поэтому в этом интервале
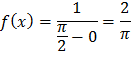
Вне рассматриваемого интервала f(x) =0.
Функция y=sin x в интервале (0; ) монотонна, следовательно, в этом интервале она имеет обратную функцию x=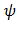 
(y)=arcsin y.
Найдем производную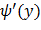 
: 
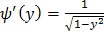
Найдем искомую плотность распределения по формуле
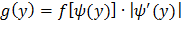
Учитывая, что f(x) = 
, следовательно,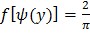 
, получим
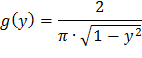
Так как y=sin x, причем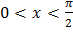 
, то 0 < y < 1.
Таким образом, в интервале (0;1) имеем
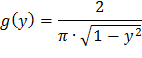
Вне этого интервала g(y)=0.
Контроль:
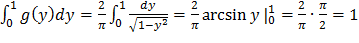
Ответ: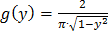 
на (0;1) и g(y)=0 вне этого интервала.
№385 Задана плотность распределения случайной величины X: f(x)= 
в интервале 
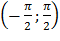; вне этого интервала f(x) =0. Найти плотность распределения g(y) случайной величины Y = tg X.
Решение:
По условию f(x)= в интервале .
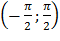Вне этого интервала f(x) =0.
Функция y=tg x в интервале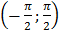 
монотонна, следовательно, в этом интервале она имеет обратную функцию x= 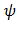(y)=arctg y.
Найдем производную :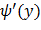 
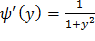
Найдем искомую плотность распределения по формуле
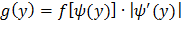
Учитывая, что f(x) = 
, следовательно,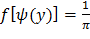 
, получим
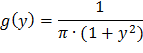
Так как y=tg x, причем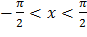 
, то -∞ < y < +∞.
Таким образом, в интервале (-∞;+∞) имеем
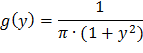
Контроль:
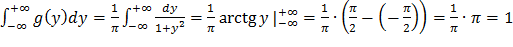
Ответ: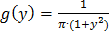 
на (-∞;+∞)
№386 Случайная величина X распределена равномерно в интервале (0; 2π). Найти плотность распределения g(y) случайной величины Y=cos X.
Решение:
Найдем плотность распределения f(x) случайной величины X
В интервале (0;2π) имеем f(x)= 
Вне этого интервала f(x)=0
Из уравнения y=cos x найдем обратную функцию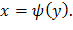 
Так как в интервале (0;2π) функция не монотонна, то разобьем этот интервал на интервалы (0; π) и (π; 2π), в которых эта функция монотонна. В интервале (0; π) обратная функция 
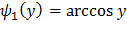; в интервале (π; 2π) обратная функция 
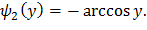Искомая плотность распределения может быть найдена из равенства
(*)
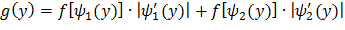Найдем производные обратных функций:
, 
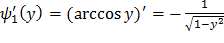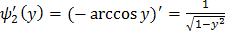
Найдем модули производных:
, 
(**)
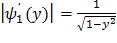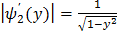Учитывая, что f(x)=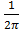 
, получим
, 
(***)
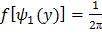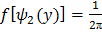Подставляя (**) и (***) в (*), имеем
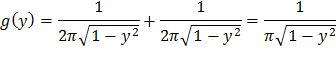
Так как y=cos x, причем 0 < x < 2π, то -1 < y < 1. Таким образом, в интервале (-1;1) искомая плотность распределения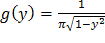 
; вне этого интервала g(y)=0.
Контроль:
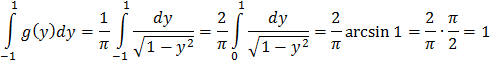
Ответ: 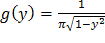в интервале (-1;1); g(y)=0 вне этого интервала.
№387 Случайная величина X распределена равномерно в интервале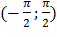 
. Найти плотность распределения g(y) случайной величины Y=cos X.
Решение:
Найдем плотность распределения f(x) случайной величины X
В интервале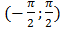 
имеем f(x)=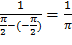 
Вне этого интервала f(x)=0
Из уравнения y=cos x найдем обратную функцию 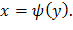Так как в интервале 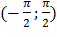функция не монотонна, то разобьем этот интервал на интервалы 
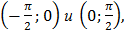в которых эта функция монотонна. В интервале 
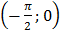обратная функция 
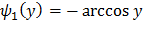; в интервале 
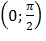обратная функция 
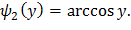Искомая плотность распределения может быть найдена из равенства
(*)
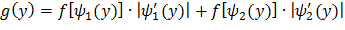Найдем производные обратных функций:
, 
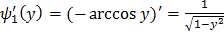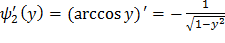
Найдем модули производных:
, (**)
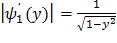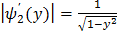Учитывая, что f(x)= , получим
, 
(***)
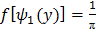Подставляя (**) и (***) в (*), имеем``
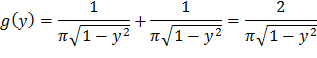
Так как y=cos x, причем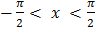 
, то 0 < y < 1. Таким образом, в интервале (0;1) искомая плотность распределения 
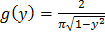; вне этого интервала g(y)=0.
Контроль:
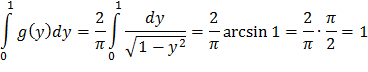
Ответ: 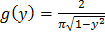в интервале (0;1); g(y)=0 вне этого интервала.
№388 Случайная величина X распределена нормально с математическим ожиданием, равным а, и средним квадратическим отклонением, равным σ. Доказать, что линейная функция Y=AX+B также распределена нормально, причем M(Y)=Aa+B и σ(Y)= | A |σ.
Решение:
Найдем плотность распределения случайной величины X:
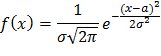
Функция y=Ax+B монотонна, поэтому применима формула
(*)
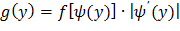Найдем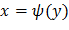 
из уравнения y=Ax+B: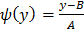 
Найдем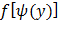 
: 
(**)
Найдем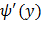 
: 
Найдем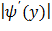 
: 
(***)
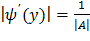Подставляя (**) и (***) в (*), имеем
Отсюда видно, что линейная функция Y=AX+B распределена нормально, причем M(Y)=Aa+B и σ(Y)= | A |σ, что и требовалось доказать.
№389 Задана плотность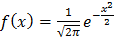 
, (- ∞< x < +∞) нормально распределенной случайной величины X. Найти плотность распределения g(x) случайной величины Y=X2.
Решение:
Из уравнения y=x2 найдем обратную функцию. Так как в интервале (- ∞; +∞) функция y=x2
не монотонна, то разобьем этот интервал на интервалы (- ∞; 0) и (0; +∞), в которых рассматриваемая функция монотонна. В интервале (- ∞; 0) обратная функция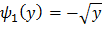 
; В интервале (0; +∞) обратная функция 
.
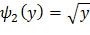Искомая плотность распределения может быть найдена из равенства
(*)
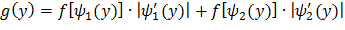Найдем производные обратных функций:
, 
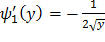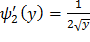
Найдем модули производных:
, 
(**)
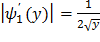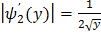Учитывая, что 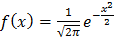, , 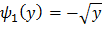, 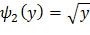получим
, 
(***)
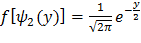Подставляя (**) и (***) в (*), имеем
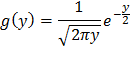
Так как y=x2, причем -∞ < x < +∞, то 0 < y < +∞.
Таким образом, в интервале (0;∞) искомая плотность распределения
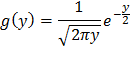
Вне этого интервала g(y)=0.
Контроль:
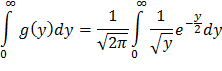
Положив y=t2 и, следовательно, dy=2t dt, получим
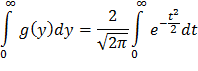
Учитывая, что интеграл Пуассона
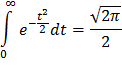
Найдем
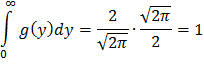
Ответ: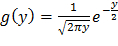 
в интервале (0;∞), g(y)=0 вне этого интервала.
№390 Задана плотность 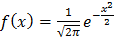нормально распределенной случайной величины X. Найти плотность распределения случайной величины Y= 
X2.
Решение:
Из уравнения y= 
x2 найдем обратную функцию. Так как в интервале (- ∞; +∞) функция y= x2
не монотонна, то разобьем этот интервал на интервалы (- ∞; 0) и (0; +∞), в которых рассматриваемая функция монотонна. В интервале (- ∞; 0) обратная функция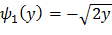 
; В интервале (0; +∞) обратная функция 
.
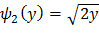Искомая плотность распределения может быть найдена из равенства
(*)
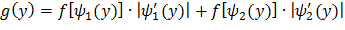Найдем производные обратных функций:
, 
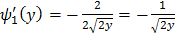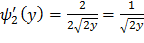
Найдем модули производных:
, 
(**)
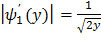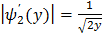Учитывая, что 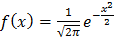, , 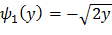, 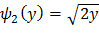получим
, 
(***)
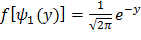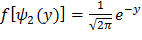Подставляя (**) и (***) в (*), имеем
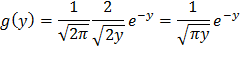
Так как y= x2, причем -∞ < x < +∞, то 0 < y < +∞.
Таким образом, в интервале (0;∞) искомая плотность распределения
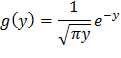
Вне этого интервала g(y)=0.
Контроль:
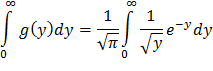
Положив y=t2 и, следовательно, dy=2t dt, получим
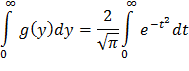
Учитывая, что интеграл Пуассона
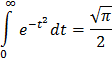
Найдем
Ответ: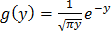 
в интервале (0;∞), g(y)=0 вне этого интервала.
№391 Задана плотность распределения 
. Найти плотность распределения g(x) случайной величины Y= 
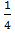X2.
Решение:
Из уравнения y=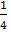 
x2 найдем обратную функцию. Так как в интервале (- ∞; +∞) функция y= 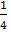x2 не монотонна, то разобьем этот интервал на интервалы (- ∞; 0) и (0; +∞), в которых рассматриваемая функция монотонна. В интервале (- ∞; 0) обратная функция 
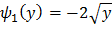; В интервале (0; +∞) обратная функция 
.
Искомая плотность распределения может быть найдена из равенства
(*)
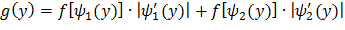Найдем производные обратных функций:
, 
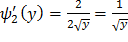
Найдем модули производных:
, 
(**)
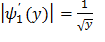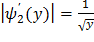Учитывая, что , , 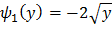, получим
, 
(***)
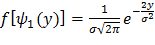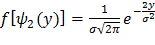Подставляя (**) и (***) в (*), имеем
Так как y= 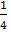x2, причем -∞ < x < +∞, то 0 < y < +∞.
Таким образом, в интервале (0;∞) искомая плотность распределения
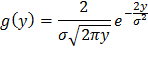
Вне этого интервала g(y)=0.
Контроль:
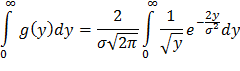
Положив y=t2 и, следовательно, dy=2t dt, получим
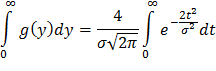
Учитывая, что интеграл Пуассона
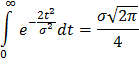
Найдем
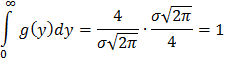
Ответ: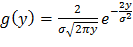 
в интервале (0;∞), g(y)=0 вне этого интервала.
№392 Случайная величина X задана плотностью распределения f(x)=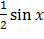 
в интервале (0; π); вне этого интервала f(x) =0. Найти математическое ожидание случайной величины Y= 
, определив предварительно плотность распределения g(Y) величины Y.
Решение:
Найдем сначала плотность g(y) случайной величины Y. Так как функция y=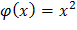 
для рассматриваемых значений 
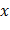(0 < x < π) строго возрастающая, то плотность g(y) будем искать по формуле ,
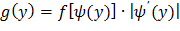Где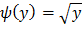 
- функция, обратная функции Y=x2. Подставляя 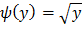и учитывая, что
f(x)= ,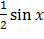 
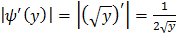, получим
Найдем математическое ожидание величины Y, учитывая, что возможные значения Y заключены в интервале (0; π2) (так как y =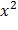 
и 0 < x < π, то 0 < y < π2):
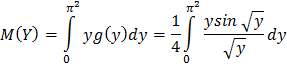
Пользуясь подстановкой y=t2 , получим
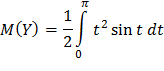
Интегрируя дважды по частям, окончательно имеем
Ответ: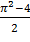 
№393 Случайная величина X задана плотностью распределения f(x)= 
в интервале (0;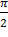 
); вне этого интервала f(x) =0. Найти математическое ожидание функции Y= .
Решение:
Подставив данные этой задачи, получаем
Ответ: 
