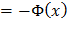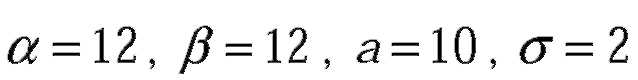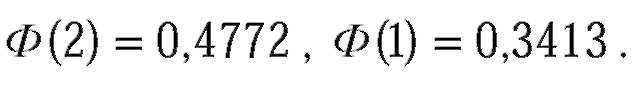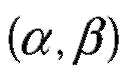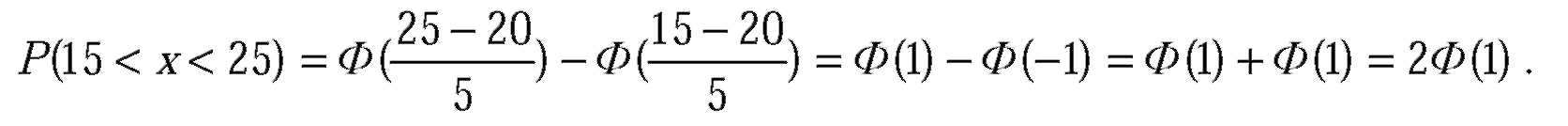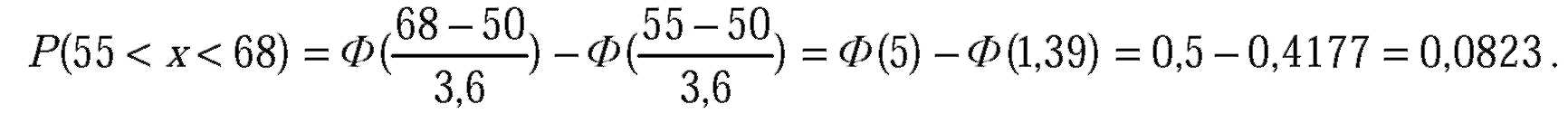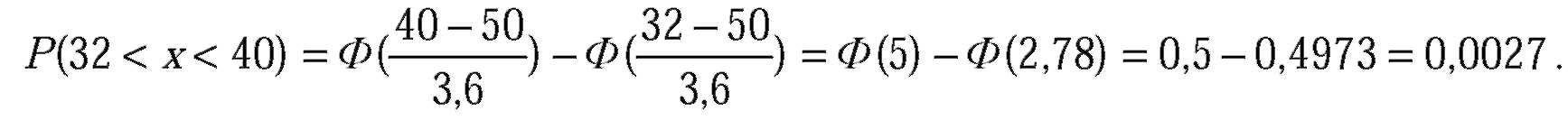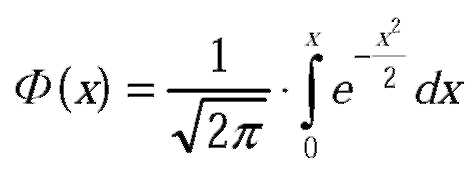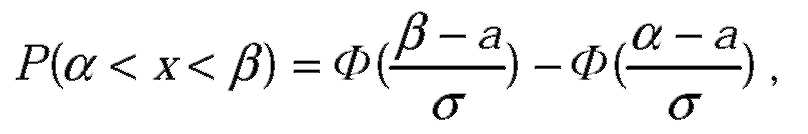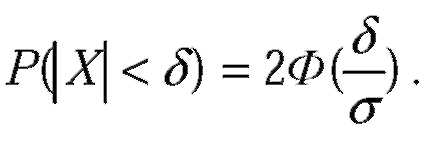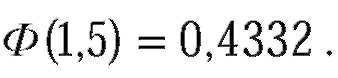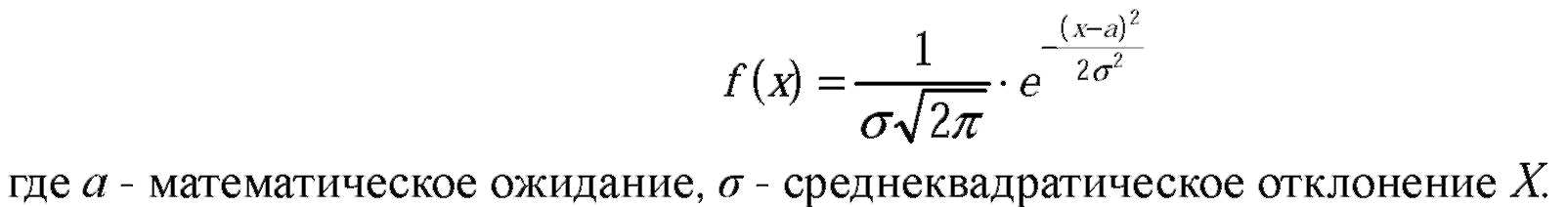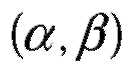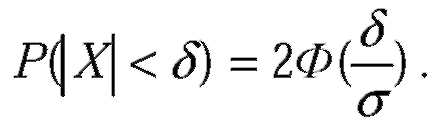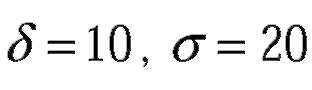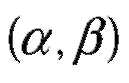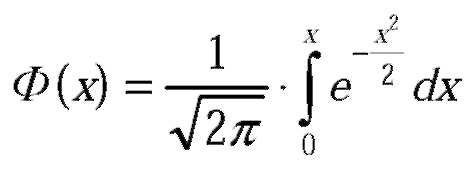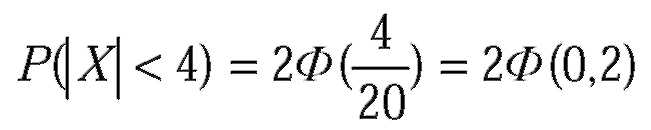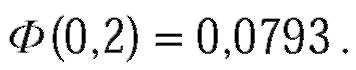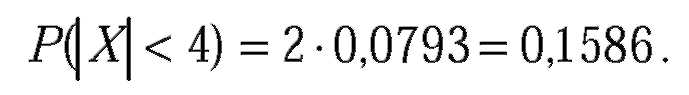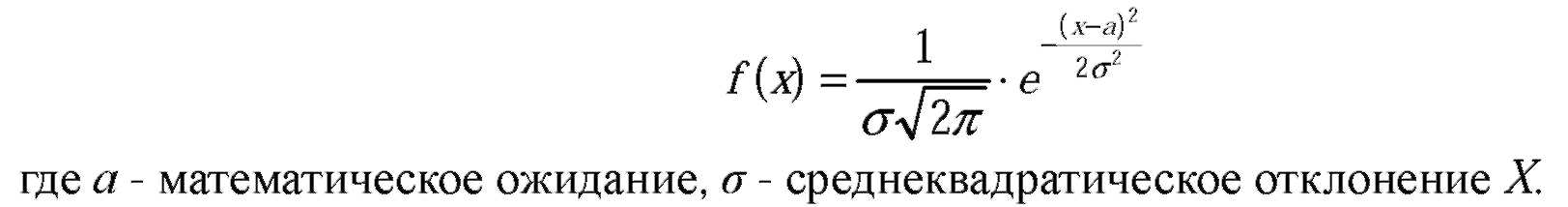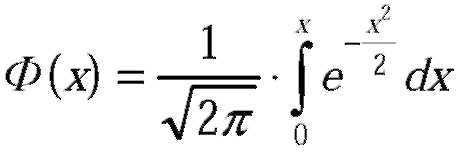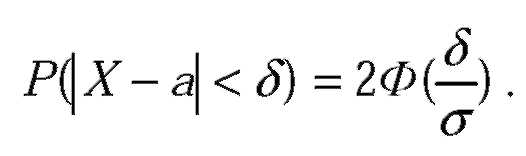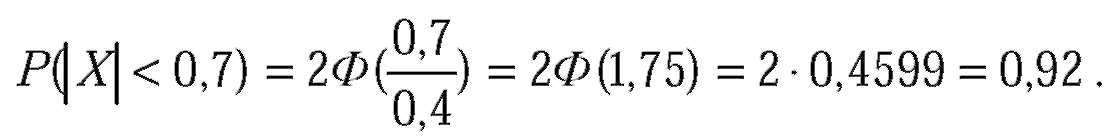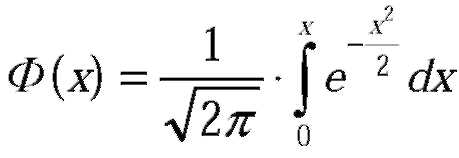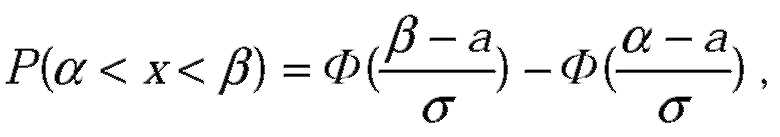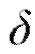Подставив φ(x)=π  /4,f(x)=1/(b-a) и выполнив интегрирование, получим
/4,f(x)=1/(b-a) и выполнив интегрирование, получим
D[π  /4]=(
/4]=( 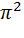 /720)
/720) 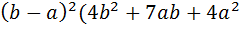 ).
).
№319 Ребро куба x измерено приближенно, причем a  . Рассматривая ребро куба как случайную величину X,распределенную равномерно в интервале (a,b),найти математическое ожидание и дисперсию объема куба.
. Рассматривая ребро куба как случайную величину X,распределенную равномерно в интервале (a,b),найти математическое ожидание и дисперсию объема куба.
Решение
1.Найдем математическое ожидание площади круга – случайной величины Y=φ(K)=  - по формуле
- по формуле
M[φ(X)]= 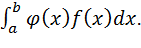
Поставив φ(x)= 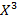 ,f(x)=1/(b-a) и выполнив интегрирование, получим
,f(x)=1/(b-a) и выполнив интегрирование, получим
M( 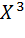 )=
)= 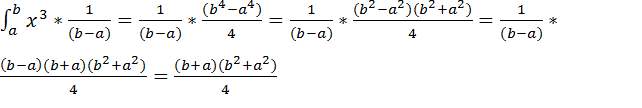 .
.
2.Найдём дисперсию площади круга по формуле
D [φ(X)]= 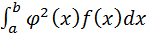 -
-  .
.
Подставив φ(x)= 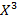 ,f(x)=1/(b-a) и выполнив интегрирование, получим
,f(x)=1/(b-a) и выполнив интегрирование, получим
D  =
= 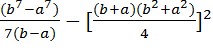 .
.
№320 Случайные величины X и Y независимы и распределены равномерно: X-в интервале (a,b),Y-в интервале (c,d).Найти математическое ожидание произведения XY.
Решение
Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий, т.е.
M(XY)= 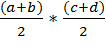
№321 Случайные величины X и Y независимы и распределены равномерно: X- в интервале (a,b), Y – в интервале (c,d). Найти дисперсию произведения XY.
Решение
Воспользуемся формулой
D(XY)=M[ 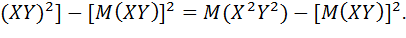
Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий, поэтому
D(XY)=M 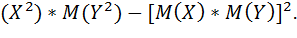 (*)
(*)
Найдем M  по формуле
по формуле
M[φ(X)]= 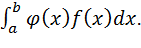
Подставляя φ(x)=  ,f(x)=1/(b-a) и выполняя интегрирование,получим
,f(x)=1/(b-a) и выполняя интегрирование,получим
M  (**)
(**)
Аналогично найдем
M 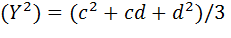 (***)
(***)
Подставив M(X)=(a+b)/2, M(Y)=(c+d)/2,а так же (***) и (**) в (*),окончательно получим
D(XY)=  -[
-[  .
.
№322 Математическое ожидание нормально распределённой случайной величины X равно a=3 и среднее квадратическое отклонение σ=2.Написать плотность вероятности X.
Решение
Воспользуемся формулой:
f(x)=  .
.
Подставляя имеющиеся значения получим:
f(x)=  = f(x)=
= f(x)=  .
.
№323 Написать плотность вероятности нормально распределенной случайной величины X, зная, что M(X)=3, D(X)=16.
Решение
Воспользуемся формулой:
f(x)=  .
.
Для того, чтобы найти значение σ воспользуемся свойством, что среднее квадратическое отклонение случайной величины X равно квадратному корню из ее дисперсии. Следовательно σ=4, M(X)=a=3. Подставляя в формулу получим
f(x)=  =
= 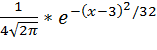 .
.
№324 Нормально распределенная случайная величина X задана плотностью
f(x)=  . Найти математическое ожидание и дисперсию X.
. Найти математическое ожидание и дисперсию X.
Решение
Воспользуемся формулой
f(x)=  ,
,
где a -математическое ожидание, σ -среднее квадратическое отклонение X. Из этой формулы следует, что a=M(X)=1. Для нахождения дисперсии воспользуемся свойством, что среднее квадратическое отклонение случайной величины X равно квадратному корню из ее дисперсии. Следовательно D(X)=  =
= 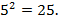
Ответ: математическое ожидание равно 1; дисперсия равна 25.
Бондарчук Родион
№ 325
Дана функция распределения нормированного нормального закона  . Найти плотность распределения f(x).
. Найти плотность распределения f(x).
Решение:
Зная, что 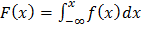 , находим f(x).
, находим f(x).
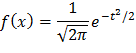
Ответ: 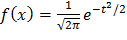
№ 327
Доказать, что функция Лапласа  . нечетна:
. нечетна:  .
.
Решение:

Произведем замену 
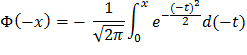
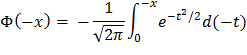
Делаем обратную замену и получаем:
 =
= 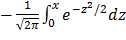 =
= 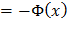
Ч.Т.Д.
| № 328Математическое ожидание и среднеквадратическое отклонение нормально распределенной случайной величины X соответственно равны 10 и 2. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (12,14).
|

| Решение: Нормальным называют распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид:
|

| Вероятность того, что X примет значение, принадлежащее интервалу
|

| Искомая вероятность равна:
|
| № 329Математическое ожидание и среднеквадратическое отклонение нормально распределенной случайной величины X соответственно равны 20 и 5. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (15,25).
|

| Решение: Нормальным называют распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид:
|

| Вероятность того, что X примет значение, принадлежащее интервалу
|
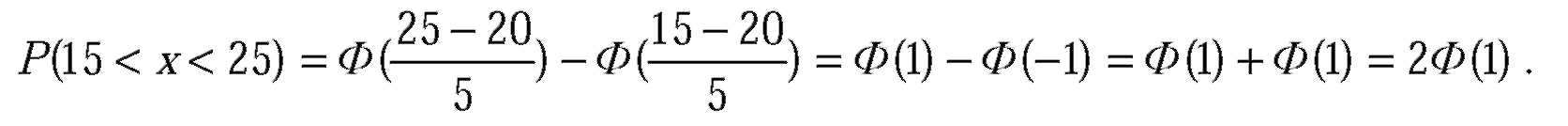
| и принимая во внимание, что
|

| Искомая вероятность равна:
|
| № 330Автомат штампует детали. Контролируется длина детали X, которая распределена нормально с математическим ожиданием (проектная длина), равным 50мм. Фактически длина изготовленных деталей не менее 32 и не более 68мм. Найти вероятность того, что длина наудачу взятой детали: а) больше 55мм; б) меньше 40мм.
|

| Решение: Нормальным называют распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид:
|

| Вероятность того, что X примет значение, принадлежащее интервалу
|
| Поскольку фактически длина изготовленных деталей не менее 32 и не более 68мм, то вероятность, что длина всех деталей заключена в интервале (32,68), равна 1, т.е.
|
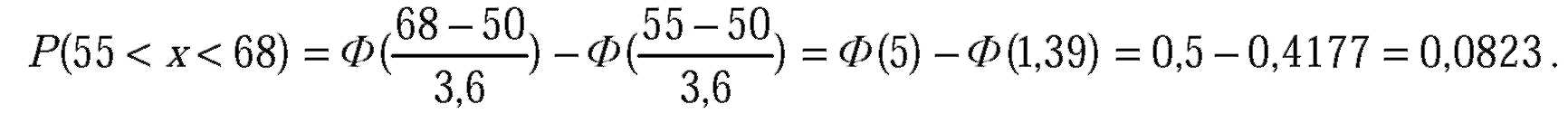
| а) Вероятность, что длина больше 55см равна:
|
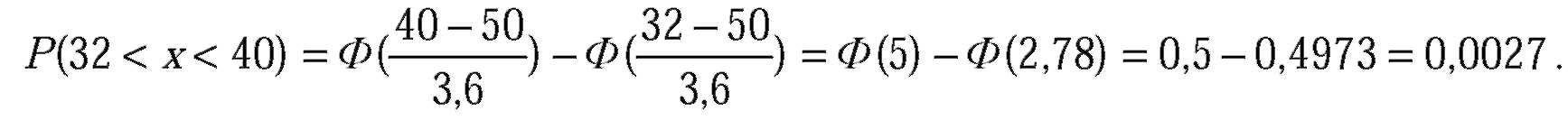
| б) Вероятность, что длина меньше 40см равна:
|
| № 331Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения X подчинены нормальному закону со среднеквадратическим отклонением о=10мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15мм.
|

| Решение: Нормальным называют распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид:
|
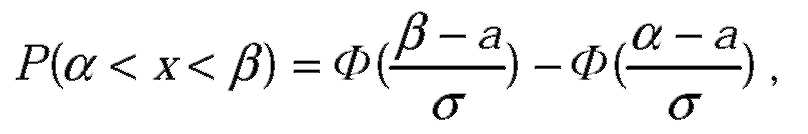
| Вероятность того, что X примет значение, принадлежащее интервалу
|
| Вероятность того, что абсолютная величина отклонения меньше положительного числа
|
| В частности, если a=0, то справедливо равенство:
|
| Математическое ожидание случайных ошибок равно нулю, поэтому применима
|


| Тогда искомая вероятность равна:
|
| № 332Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со среднеквадратическим отклонением а=20г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10г.
|
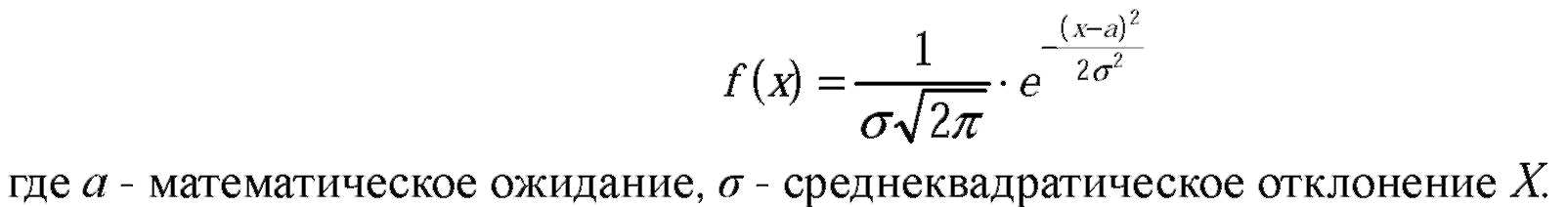
| Решение: Нормальным называют распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид:
|

| Вероятность того, что X примет значение, принадлежащее интервалу
|
| Вероятность того, что абсолютная величина отклонения меньше положительного числа
|
| В частности, если a=0, то справедливо равенство:
|
| Математическое ожидание случайных ошибок равно нулю, поэтому применима
|


| Тогда искомая вероятность равна:
|
| № 333Случайные ошибки измерения подчинены нормальному закону со среднеквадратическим отклонением о=20мм и математическим ожиданием а=0. Найти вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдет по абсолютной величине 4мм.
|

| Решение: Нормальным называют распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид:
|

| Вероятность того, что X примет значение, принадлежащее интервалу
|
| Вероятность того, что абсолютная величина отклонения меньше положительного числа
|
| В частности, если a=0, то справедливо равенство:
|
| Найдем для начала вероятность того, что ошибка не превзойдет по абсолютной величине 4мм, при одном испытании.
|
| Математическое ожидание a = 0, поэтому применима формула:
|
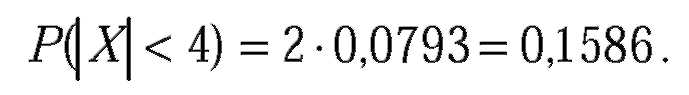
| Тогда искомая вероятность равна:
|
| Пусть А - событие состоит в том, что из трех независимых измерений ошибка хотя бы одного не превзойдет по абсолютной величине 4мм, причем p = 0,1586. Это означает, что ошибка не превзойдет 4мм. либо при одном измерении, либо при двух, либо при трех измерениях. Однако, вероятность искомого события можно найти, рассмотрев противоположное событие - ни при одном измерении ошибка не превзойдет 4мм, т.е. по формуле Бернулли (p = 0,1586, q = 1 - 0,1586 = 0,8414):
|
| Тогда вероятность события А равна:
|
| № 334Автомат изготовляет шарики. Шарик считается годным, если отклонение X диаметра шарика от проектного размера по абсолютной величине меньше 0,7мм. Считая, что случайная величина X распределена нормально со среднеквадратическим отклонением о=0,4мм, найти, сколько в среднем будет годных шариков среди ста изготовленных.
|
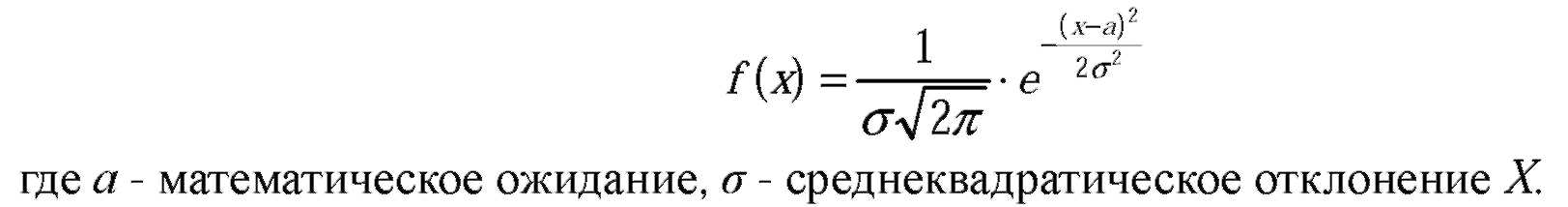
| Решение: Нормальным называют распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид:
|

| Вероятность того, что X примет значение, принадлежащее интервалу
|
| Вероятность того, что абсолютная величина отклонения меньше положительного числа
|
| В частности, если a=0, то справедливо равенство:
|
| Так как X - отклонение (диаметра шарика от проектного размера), то
|
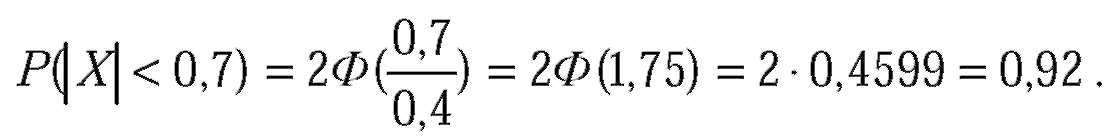
| Таким образом, вероятность отклонения, меньшего 0,7мм, равна 0,92. Отсюда следует, что примерно 92 шарика из 100 окажутся годными.
|
| № 335Деталь, изготовленная автоматом, считается годной, если отклонение ее контролируемого размера от проектного не превышает 10мм. Случайные отклонения контролируемого размера от проектного подчинены нормальному закону со среднеквадратическим отклонением а=5мм и математическим ожиданием a=0. Сколько процентов годных деталей изготавливает автомат?
|

| Решение: Нормальным называют распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид:
|
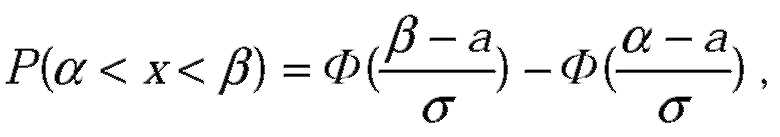
| Вероятность того, что X примет значение, принадлежащее интервалу
|
| Вероятность того, что абсолютная величина отклонения меньше положительного числа
|
 /4,f(x)=1/(b-a) и выполнив интегрирование, получим
/4,f(x)=1/(b-a) и выполнив интегрирование, получим /4]=(
/4]=( 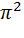 /720)
/720) 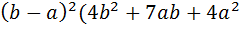 ).
). . Рассматривая ребро куба как случайную величину X,распределенную равномерно в интервале (a,b),найти математическое ожидание и дисперсию объема куба.
. Рассматривая ребро куба как случайную величину X,распределенную равномерно в интервале (a,b),найти математическое ожидание и дисперсию объема куба. - по формуле
- по формуле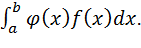
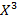 ,f(x)=1/(b-a) и выполнив интегрирование, получим
,f(x)=1/(b-a) и выполнив интегрирование, получим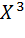 )=
)= 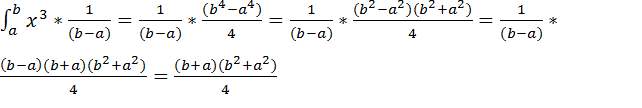 .
.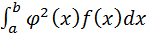 -
-  .
.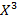 ,f(x)=1/(b-a) и выполнив интегрирование, получим
,f(x)=1/(b-a) и выполнив интегрирование, получим =
= 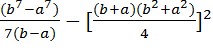 .
.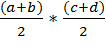
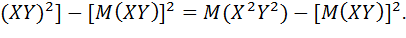
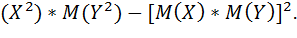 (*)
(*) по формуле
по формуле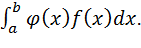
 ,f(x)=1/(b-a) и выполняя интегрирование,получим
,f(x)=1/(b-a) и выполняя интегрирование,получим (**)
(**)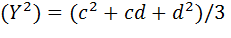 (***)
(***) -[
-[  .
. .
. = f(x)=
= f(x)=  .
. .
. =
= 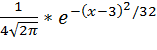 .
. . Найти математическое ожидание и дисперсию X.
. Найти математическое ожидание и дисперсию X. ,
, =
= 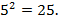
 . Найти плотность распределения f(x).
. Найти плотность распределения f(x).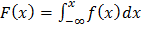 , находим f(x).
, находим f(x).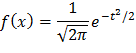
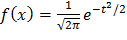
 . нечетна:
. нечетна:  .
.

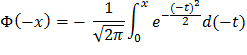
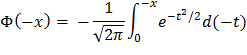
 =
= 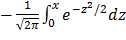 =
=