величина Y приняла значение Y = 1, достаточно, чтобы величина X
приняла значение Х = —1 или Х = 1. Последние два события несовместны,
их вероятности соответственно равны 0,3 и 0,2. Поэтому вероятность события Y = 1 по теореме сложения
P(Y = 1) = P (X = —1) + Р (Х = 1)=0,3+0,2 = 0,5.
Аналогично найдем вероятность возможного значения Y = 4:
P(Y = 4) = P (X = —2) + Р (Х = 2)=0,1+0,4 = 0,5.
Напишем искомый закон распределения величины Y:
Y 1 4
р 0,5 0,5
№376. Дискретная случайная величина X задана законом
распределения:
X 
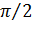
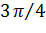
p 0,2 0,7 0,1
Найти закон распределения случайной величины 
Решение.
Найдем возможные значения Y:


Итак, различным значениям X соответствуют одинаковые значения
Y. Это объясняется тем, что возможные значения X принадлежат
интервалу, на котором функция 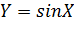 не монотонна.
не монотонна.
Найдем вероятности возможных значений Y. Для того чтобы
величина Y приняла значение Y = 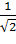 , достаточно, чтобы величина X
, достаточно, чтобы величина X
приняла значение Х =  или Х =
или Х = 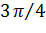 . Последние два события несовместны, их вероятности соответственно равны 0,2 и 0,1. Поэтому вероятность события Y =
. Последние два события несовместны, их вероятности соответственно равны 0,2 и 0,1. Поэтому вероятность события Y = 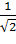 по теореме сложения
по теореме сложения
P(Y = 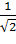 ) = P (Х =
) = P (Х =  ) + Р (Х =
) + Р (Х = 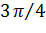 )=0,2+0,1 = 0,3.
)=0,2+0,1 = 0,3.
Для того чтобы Y = 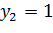 достататочно, чтобы величина X приняла значение
достататочно, чтобы величина X приняла значение 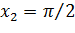 . Вероятность же события X=
. Вероятность же события X= 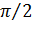 по условию равна 0,7. Следовательно, и вероятность события Y =
по условию равна 0,7. Следовательно, и вероятность события Y = 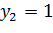 также равна 0,7.
также равна 0,7.
Напишем искомый закон распределения величины Y:
Y 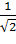 1
1
р 0,3 0,7
№377. Задана плотность распределения f(x) случайной величины X, возможные значения которой заключены в интервале (a,b). Найти плотность распределения случайной величины Y = 3 Х.
Решение.
Так как функция у=3х дифференцируемая и строго
возрастает, то применима формула
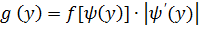 (*)
(*)
где  — функция, обратная функции у=3х.
— функция, обратная функции у=3х.
Найдем  :
:
 =x=у/3.
=x=у/3.
Найдем 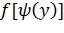 :
:
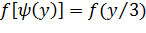 (**)
(**)
Найдем производную 

Очевидно, что:
 =
=  (***)
(***)
Найдем искомую плотность распределения, для чего подставим (**) и (***) в (*): 
Так как x изменяется в интервале (a,b) и у=3х то 3a<y<3b
№378. Задана плотность распределения f(x) случайной величины X, возможные значения которой заключены в интервале (a,b). Найти плотность распределения случайной величины Y, еслиа) Y =  3Х; б) Y=AX+B.
3Х; б) Y=AX+B.
Решение.
a) Так как функция у=  3х дифференцируемая и строго
3х дифференцируемая и строго
убывает, то применима формула
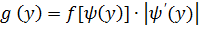 (*)
(*)
где  — функция, обратная функции у=
— функция, обратная функции у=  3х.
3х.
Найдем  :
:
 =x=
=x=  у/3.
у/3.
Найдем 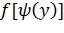 :
:
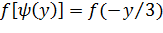 (**)
(**)
Найдем производную 
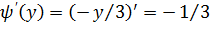
Очевидно, что:
 =
=  (***)
(***)
Найдем искомую плотность распределения, для чего подставим (**) и (***) в (*): 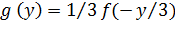
Так как x изменяется в интервале (a,b) и у=  3х то
3х то  3b<y<
3b<y<  3a
3a
б) Так как функция у= 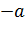 х+b дифференцируемая и строго
х+b дифференцируемая и строго
возрастает при a>0 (строго убывает при a<0), то применима формула
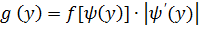 (*)
(*)
где  — функция, обратная функции у=
— функция, обратная функции у= 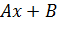
Найдем  :
:
 =x=
=x= 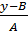 .
.
Найдем 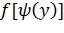 :
:
 (**)
(**)
Найдем производную 
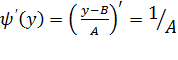
Очевидно, что:
 =
=  (***)
(***)
Найдем искомую плотность распределения, для чего подставим (**) и (***) в (*): 
Так как x изменяется в интервале (a,b) и у= ax+b, то
Aa+B<y<Ab+B, A>0 и Ab+B<y<Aa+B, A<0
№379. Случайная величина X распределена по закону Коши
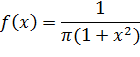
Найти плотность распределения случайной величины 
Решение:
Так как функция  дифференцируемая и строго
дифференцируемая и строго
возрастает, то применима формула
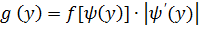 (*)
(*)
где  — функция, обратная функции у=
— функция, обратная функции у= 
Найдем  :
:

Найдем 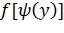 :
:
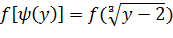 =
=  (**)
(**)
Найдем производную 
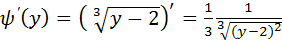
Очевидно, что:
 =
=  (***)
(***)
Найдем искомую плотность распределения, для чего подставим (**) и (***) в (*):

№380. Задана плотность распределения f(x) случайной величины X, возможные значения которой заключены в интервале (0,  ). Найти плотность распределения g(y) случайной величины Y, еслиа) Y =
). Найти плотность распределения g(y) случайной величины Y, еслиа) Y =  ; б) Y=
; б) Y= 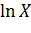 ;
;
в) Y = 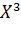 ; г) Y =
; г) Y = 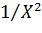 ; д) Y =
; д) Y =  ;
;
Решение:
Т.к. все функции в примерах а)-д) дифференцируемы и строго возрастают или строго убывают, то во всех случаях мы можем воспользоваться формулой:
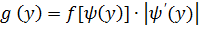 (*),
(*),
где  — функция, обратная данным функциям.
— функция, обратная данным функциям.
Найдем функцию  для всех данных примеров.
для всех данных примеров.
а)  =x=ln y
=x=ln y
б)  =x=
=x= 
в)  =x=
=x= 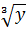
г)  =x=
=x= 
д)  =x=
=x= 
Для данных примеров найдем 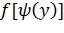 :
:
(**)
а) 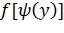 =
= 
б) 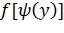 =
= 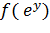
в) 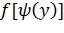 =
= 
г) 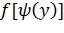 =
= 
д) 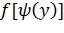 =
= 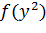
Найдём производную  для данных примеров
для данных примеров
а) 
б) 
в) 
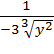
г) 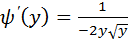
д) 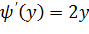
Очевидно, что:
(***)
а)  =
= 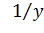
б)  =
= 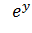
в)  =
= 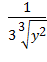
г)  =
= 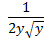
д)  =
= 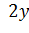
Найдем искомую плотность распределения, для чего подставим (**) и (***) в (*):
а) 
б) 
в) 
г) 
д) 
Так как x изменяется в интервале (0,  ) то
) то
а) 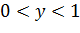
б) 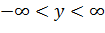
в) 
г) 
д) 
№381. Задана плотность распределения f(x) случайной величины X, возможные значения которой заключены в интервале (  ,
,  ). Найти плотность распределения g(y) случайной величины Y, еслиа) Y =
). Найти плотность распределения g(y) случайной величины Y, еслиа) Y =  ;
;
б) Y= 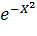 ; в) Y =
; в) Y =  ; г) Y =
; г) Y = 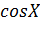 ; д) Y =
; д) Y =  ; е)
; е) 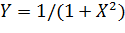
Решение:
Среди данных функций лишь функция в примере д) является дифференцируемой и строго возрастающей. Следовательно, применима формула:
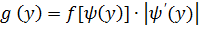 (*)
(*)
где  — функция, обратная функции у=
— функция, обратная функции у= 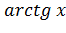
Найдем  :
:

Найдем 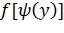 :
:
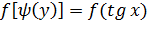 (**)
(**)
Найдем производную 
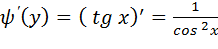
Очевидно, что:
 =
=  (***)
(***)
Найдем искомую плотность распределения, для чего подставим (**) и (***) в (*):
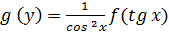 ,
,
так как 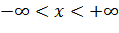 , то
, то 
Функции из примеров а)-в) и е) в интервале возможных значений X не являются монотонными, однако данные функции монотонны в двух интервалах ( ) и (
) и (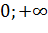 ). Тогда для вычисления плотности распределения случайной величины Y воспользуемся формулой:
). Тогда для вычисления плотности распределения случайной величины Y воспользуемся формулой:
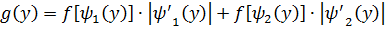 (*),
(*),
где  – функция обратная данной в интервале (
– функция обратная данной в интервале ( ),
), 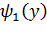 - обратная функция в интервале (
- обратная функция в интервале (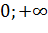 ).
).
Найдем функции 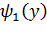 и
и  для примеров а)-в) и е):
для примеров а)-в) и е):
а) 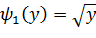
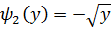
б) 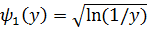
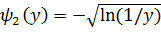
в) 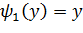
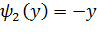
е) 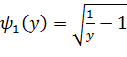
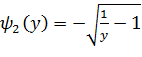
Найдем 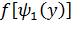 и
и  : (**)
: (**)
а) 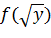
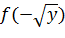
б) 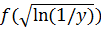

в) 

е) 
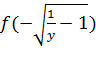
Очевидно, что  =
= 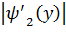 . Найдем
. Найдем  : (***)
: (***)
а) 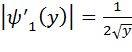
б) 
в) 
е) 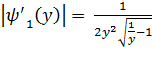
Подставляя (***) и (**) в (*) получим:
а) 
б) 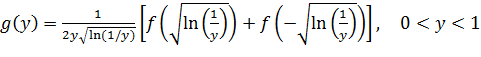
в) 
е) 
В примере г) функция является периодической, с периодом 2 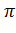 , поэтому рассмотрим данную функцию на интервале
, поэтому рассмотрим данную функцию на интервале  .
.
На данном интервале функция не является монотонной, однако данная функция является монотонной на двух интервалах  и
и 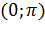 . Тогда для вычисления плотности распределения случайной величины Y воспользуемся формулой:
. Тогда для вычисления плотности распределения случайной величины Y воспользуемся формулой:
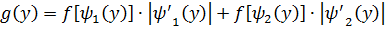 (*),
(*),
где  – функция обратная данной в интервале
– функция обратная данной в интервале  ,
, 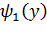 - обратная функция в интервале
- обратная функция в интервале 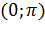 .
.
Найдем функции 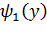 и
и  :
:
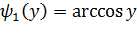
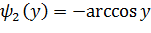
Найдем 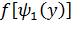 и
и  : (**)
: (**)

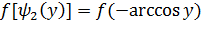
Очевидно, что  =
= 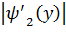 . Найдем
. Найдем  : (***)
: (***)

Подставляя (***) и (**) в (*) получим:

Обобщим теперь данную формулу на интервал (  ,
,  ), получим:
), получим:
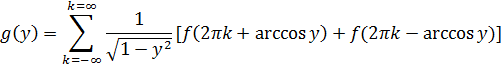
№382. В прямоугольной системе координат хОу из точки А (4; 0) наудачу (под произвольным углом t) проведен луч, пересекающий ось Оу. Найти дифференциальную функцию g(y) распределения вероятностей ординаты у точки пересечения проведенного луча с осью Оу.
Решение:
Угол t можно рассматривать как случайную величину, распределенную равномерно в интервале 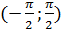 , причем в этом интервале плотность распределения
, причем в этом интервале плотность распределения

вне рассматриваемого интервала f(t)=0.
Из рисунка 1 следует, что ордината у связана с углом t следующей зависимостью: y=4tg t. Эта функция в интервале 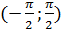 монотонно
монотонно
возрастает, поэтому для отыскания искомой плотности распределения g(y) применима формула.
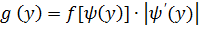 (*)
(*)




