№394 Случайная величина X задана плотностью распределения f(x)= 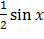 в интервале (0; π); вне этого интервала f(x) =0. Найти дисперсию функции Y=
в интервале (0; π); вне этого интервала f(x) =0. Найти дисперсию функции Y=  , используя плотность распределения g(Y).
, используя плотность распределения g(Y).
Решение:
Используем формулу
 ,
,
Где c и d – концы интервала, в котором заключены возможные значения Y.
Подставляя


(см. задачу №392)
И учитывая, что с=0, d=π2 (так как  и
и  , получим
, получим
 (*)
(*)
Интегрируя сначала с помощью подстановки y=t2 , а потом четырежды по частям, имеем
 (**)
(**)
Подставив (**) в (*), окончательно получим

Ответ: 
Митько Дмитрий
№395 Случайная величина Х задана плотностью распределения 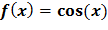 в интервале
в интервале  ; вне этого интервала
; вне этого интервала  . Найти дисперсию функции
. Найти дисперсию функции  .
.
Решение:
Используем формулу  , где c и d – концы интервала, в котором заключены возможные значения Y. Подставляя
, где c и d – концы интервала, в котором заключены возможные значения Y. Подставляя  ,
,  и учитывая, что
и учитывая, что 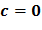 и
и  , получим
, получим




№396 Ребро куба измерено приближенно, причем  . Рассматривая ребро куба как случайную величину Х, распределенную равномерно в интервале
. Рассматривая ребро куба как случайную величину Х, распределенную равномерно в интервале  , найти: а) математическое ожидание объёма куба; б) дисперсию объема куба.
, найти: а) математическое ожидание объёма куба; б) дисперсию объема куба.
Решение:
Плотность распределения случайной величины  равна
равна  .
.
а) Найдем математическое ожидание: 
б) Найдем дисперсию:  ;
;

№397 Задана функция распределения  случайной величины Х. Найти функцию распределения
случайной величины Х. Найти функцию распределения  случайной величины
случайной величины 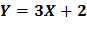 .
.
Решение:
По определению функции распределения,  . Поскольку функция
. Поскольку функция  – возрастающая, то неравенство
– возрастающая, то неравенство 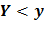 выполняется, если имеет место неравенство
выполняется, если имеет место неравенство  , поэтому
, поэтому
 ,
,
Из уравнения  выразим
выразим  :
:  .
.
Получим 
№398 Задана функция распределения  случайной величины Х. Найти функцию распределения
случайной величины Х. Найти функцию распределения  случайной величины
случайной величины  .
.
Решение:
Поскольку функция  – убывающая, то неравенство
– убывающая, то неравенство 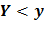 выполняется, если имеет место неравенство
выполняется, если имеет место неравенство  , поэтому
, поэтому 
События  и
и  противоположны, поэтому сумма вероятностей этих событий равна единице.
противоположны, поэтому сумма вероятностей этих событий равна единице.  , следовательно,
, следовательно,  .
.
Из уравнения  выразим
выразим  :
:  .
.
Подставив  , окончательно получим:
, окончательно получим:  .
.
№399 Задана функция распределения  случайной величины Х. Найти функцию распределения
случайной величины Х. Найти функцию распределения  случайной величины
случайной величины  , если а)
, если а)  ; б)
; б)  ; в)
; в)  .
.
Решение
а)  . См задачу №397.
. См задачу №397.
б) 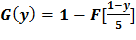 . См задачу №398.
. См задачу №398.
в) Если  , тогда ответ аналогичен ответу в задаче 398:
, тогда ответ аналогичен ответу в задаче 398: 
Если  , тогда ответ аналогичен ответу в задаче 397:
, тогда ответ аналогичен ответу в задаче 397: 
№400 Дискретные независимые случайные величины 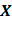 и
и  заданы распределениями:
заданы распределениями:


Найти распределение величины  .
.
Решение:
Для того, чтобы составить распределение величины  , надо найти все возможные значения
, надо найти все возможные значения  и их вероятности.
и их вероятности.
Возможные значения  есть суммы каждого возможного значения
есть суммы каждого возможного значения 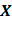 с каждым возможным значением
с каждым возможным значением  :
:  ;
;  ;
;  ;
;  .
.
Найдем вероятности этих возможных значений. Для того, чтобы 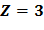 , достаточно чтобы Х=1 и Y=2. Так как Х и Y независимы, то вероятность этого события находим по правилу умножения:
, достаточно чтобы Х=1 и Y=2. Так как Х и Y независимы, то вероятность этого события находим по правилу умножения:




Напишем искомое распределение:



Ответ:
Z 3 5 7
P 0.18 0.54 0.28
№401 Дискретные случайные величины Х и Y заданы распределениями:
а) Х 10 12 16 Y 1 2
Р 0,4 0,1 0,5 P 0.2 0.8
б) Х 4 10 Y 1 7
Р 0,7 0,3 P 0.8 0.2
Найти распределение случайной величины  .
.
Решение:
а)  ;
;  ;
;  ;
;  ;
;  ;
; 






б) 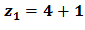 ;
;  ;
;  ;
;  .
.




Ответ:
а) Z 11 12 13 14 17 18
P 0.08 0.32 0.02 0.08 0.1 0.4
б) Z 5 11 17
P 0.56 0.38 0.06
№402 Независимые случайные величины X и Y заданы плотностями распределений:
 ,
, 
Найти композицию этих законов, т.е. плотность распределения случайной величины  .
.
Решение:
Так как возможные значения аргументов неотрицательны, то применима формула:  .
.
Следовательно, 
Выполнив элементарные преобразования, получим 
Здесь  , так как
, так как  и возможные значения Х и Y неотрицательны.
и возможные значения Х и Y неотрицательны.
Итак, 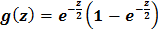 в интервале
в интервале  , вне этого интервала
, вне этого интервала 
№403 Независимые случайные величины X и Y заданы плотностями распределений:
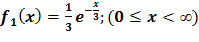 ,
, 
Найти композицию этих законов, т.е. плотность распределения случайной величины  .
.
Решение:
Так как возможные значения аргументов неотрицательны, то применима формула:  .
.
Следовательно, 
Выполнив элементарные преобразования, получим 
№404 Независимые нормально распределенные случайные величины Х и Y заданы плотностями распределений:

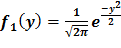
Доказать, что композиция этих законов, т.е. плотность распределения случайной величины  , также есть нормальный закон.
, также есть нормальный закон.
Решение:
Используем формулу  .
.
Тогда 
Выполнив элементарные выкладки, получим 
Учитывая, что интеграл Пуассона, стоящий в правой части равенства, равен  , окончательно имеем
, окончательно имеем  .
.
В рассматриваемой задаче легко убедиться, что  и
и  .
.
Олейников Илья
№407 Заданны плотности распределений равномерно распределенных независимых случайных величин X и Y: f1(x)=1/2 в интервале (1,3), вне этого интервала f1(x)=0, f2(y)=1/4 в интервале (1,6), вне этого интервала f2(y)=0. Найти функцию распределения и плотность распределения случайной величины Z=X+Y. Построить график плотности распределения g(z).
Решение.
По условию, возможные значения X определяются неравенством 1<x<3, возможные значения Y неравенством 1<y<6. Отсюда следует, что возможные случайные точки (X;Y) расположены в прямоугольнике OABC
y
6 A B
0 3 C x
По определению, функция распределения G(z)=P(Z<z)=P(X+Y<z).
Неравенству x+y<z удовлетворяют те точки (X,Y) плоскости xOy, которые лежат ниже прямой x+y=z; если же брать только возможные значения x и y, то неравенство x+y<z выполняется только для точек, лежащих в прямоугольнике OABC ниже прямой x+y=z.
С другой стороны, так как величины X и Y независимы, то
G(z)=∫ ∫ f1(x)·f2(x)dxdy=1/8∫ ∫ dxdy=1/8·s,
(S) (S)
где s- величина той части площади прямоугольника OABC, которая лежит ниже прямой x+y=z. Очевидно, величина площади S зависит от значения z.
Искомая функция распределения:
G(z)={0,при z<3;((z-3)^2)/16,при 3<z<5;(z/4)-1,при 5<z<7;1-((9-z)^2)/16,при 7<z<9;1,при z>9}
Плотность распределения:
g(z)={0, при z<3;(z-3)/8, при 3<z<5;1/4, при 5<z<7;(9-z)/8, при 7<z<9;0,z>9}
№408 Задано распределение вероятностей дискретной случайной величины
| Y | X | ||
| 0,17 | 0,13 | 0,25 | |
| 0,10 | 0,30 | 0,05 |
Найти законы распределения составляющих X и Y.
Решение.
Сложив вероятности «по столбцам», получим вероятности возможных значений X:
p(3) =0,27, p(10)=0,43, p(12)=0,30.
Напишем закон распределения составляющей X:
X 3 10 12
p 0,27 0,43 0,30
Сложив вероятности «по строкам», аналогично найдем распределения составляющей Y:
Y 4 5
p 0,55 0,45
№409 Задано распределение вероятностей дискретной случайной величины
| Y | X | |||
| 2,3 | 0,05 | 0,12 | 0,08 | 0,04 |
| 2,7 | 0,09 | 0,30 | 0,11 | 0,21 |
Найти законы распределения составляющих
Решение.
Сложив вероятности «по столбцам», получим вероятности возможных значений X:
p(20)=0,14, p(30)=0,42, p(41)=0,19, p(50)=0,25.
Напишем закон распределения составляющей X:
X 20 30 41 50
p 0,14 0,42 0,19 0,25
Сложив вероятности «по строкам», аналогично найдем распределения составляющей Y:
Y 2,3 2,7
p 0,29 0,71
№410 Задана функция распределения двумерной случайной величины
F(x,y)={sin x ·sin y, при 0≤x≤π/2, 0≤y≤π/2; 0, при x<0 или y<0.
Найти вероятность попадания случайной точки (X,Y) в прямоугольник, ограниченный прямыми x=0, x=π/4, y=π/6, y=π/3.
Решение.
Используем формулу P(x1<X<x2, y1<Y<y2)=[F(x2,y2)-F(x1,y2)]- [F(x2,y1)-F(x1,y1)].
Положив x1=0, x2=π/4, y1= π/6, y2= π/3, получим
P=[sin(π/4)sin(π/3)-sin(0)sin(π/3)]- [sin(π/4)sin(π/6)-sin(0)sin(π/6)]=(√6-√2)/4=0,26.
№411 Найти вероятность попадания случайной точки (X,Y) в прямоугольник, ограниченный прямыми x=1, x=2, y=3, y=5, если известна функция распределения
F(x,y)={1 -2^ ¯x -2^¯y +2^¯x¯y), при x≥0, y≥0; 0, при x<0 или y<0.
Решение.
Используем формулу P(x1<X<x2, y1<Y<y2)=[F(x2,y2)-F(x1,y2)]- [F(x2,y1)-F(x1,y1)].
Положив x1=1, x2=2, y1= 3, y2= 5, получим
P=[(1 -2^ ¯2 -2^¯5 +2^¯2¯5)- (1 -2^ ¯1 -2^¯5 +2^¯1¯5)]-[(1 -2^ ¯2 -2^¯3 +2^¯2¯3)-(1 -2^ ¯1 -2^¯3 +2^¯1¯3)]= [93/128 – 31/64]-[21/32 – 7/16]=(31-28)/128=3/128.
№412 Задана функция распределения двумерной случайной величины
F(x,y)={1 -3^ ¯x -3^¯y +3^¯x¯y), при x≥0, y≥0; 0, при x<0 или y<0.
Найти двумерную плотность вероятности системы.
Решение.
Используем формулу f(x,y)=d²F/dx·dy. Найдем частные производные
dF/dx=ln3·(3^ ¯x -3^¯x¯y), d²F/dx·dy=ln²3·3^¯x¯y.
Итак, искомая двумерная плотность вероятности
f(x,y)={ ln²3·3^¯x¯y, при x≥0, y≥0; 0, при x<0 или y<0.
№413 Задана функция распределения двумерной случайной величины
F(x,y)={(1-e¯4x)(1-e¯2y), при x>0, y>0; 0, при x<0, y<0.
Найти двумерную плотность вероятности системы.
Решение.
Используем формулу f(x,y)=d²F/dx·dy. Найдем частные производные
dF/dx=4e¯4x ·(1-e¯2y), d²F/dx·dy=8e¯4x¯2y.
Итак, искомая двумерная плотность вероятности
f(x,y)={ 8e¯4x¯2y, при x>0, y>0; 0, при x<0, y<0.
№414 Задана двумерная плотность вероятности системы случайных величин (X,Y)
f(x,y)=20/(p^2(16+x^2)(25+y^2))
Найти функцию распределения системы.
Решение.
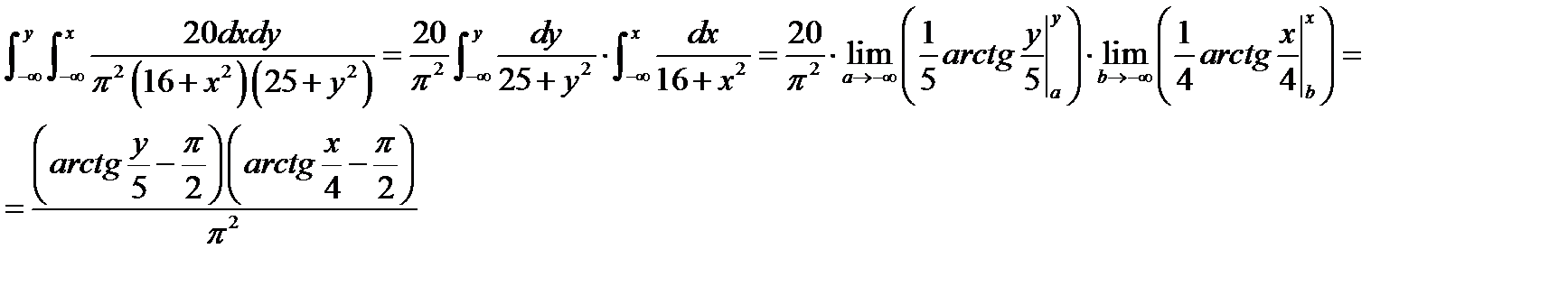
№415 Задана двумерная плотность вероятности системы случайных величин: f(x,y)=(1/2)*sin(x+y) в квадрате 0<=x<=p/2, 0<=y<=p/2; вне квадрата f(x,y)=0.
Найти функцию распределения системы.
Решение.
π/2 π/2
∫ ∫ sin(x+y)dxdy=1/2(sin(x)+sin(y)-sin(x+y))
0 0
№416 В круге x²+y²≤R² двумерная плотность вероятности f(x,y)=C(R-√(x²+y²)); вне круга f(x,y)=0. Найти: а) Постоянную C; б) вероятность попадания случайной точки (X,Y) в круг радиусом r=1 с центром в начале координат, если R=2.
Решение.
а) Используем второе свойство двумерной плотности вероятности:
∫ ∫ C(R-√(x²+y²))dxdy=1
(D)
Отсюда, перейдя к полярным координатам, получим
0 R
С=1/ ∫ dφ ∫(R-p)p dp=3/(π³)
2π 0
б)По условию, R=2; следовательно, C=3/(8π) и f(x,y)=3/(8π)·(2-√(x²+y²)).
Вероятность попадания случайной точки (X,Y) в круг радиуса r=1 с центром в начале координат (область D1)
P[(X,Y)cD1]=3/(8π)∫ ∫(2-√(x²+y²))dxdy
(D1)
Перейдя к полярным координатам, окончательно получим искомую вероятность
2π 1
P=3/(8π) ∫ dφ ∫ (2-p)p dp=1/2.
0 0
№418 Задана двумерная плотность вероятности f(x,y)=C/[(9+x^2)(16+y^2)] системы (X,Y) двух случайных величин. Найти постоянную С.
Решение.

Пискунов Игорь
№419 Задана двумерная плотность вероятности:

системы (X,Y) двух случайных величин. Найти постоянную C.
Решение:
Используем свойство двумерной вероятности 

Вычислим интеграл:
 переход к полярным координатам =
переход к полярным координатам =  Найдем
Найдем 
Ответ: 
№420 В первом квадранте задана функция распределения системы двух случайных величин:

Найти: а) двумерную плотность вероятности системы; б) вероятность попадания
случайной точки (X,Y) в треугольник с вершинами A(1;3), B(3;3), C(2;8).
Решение:
а) Используем формулу:  Найдем частные производные:
Найдем частные производные:


Итак, искомая двумерная плотность вероятности равна:
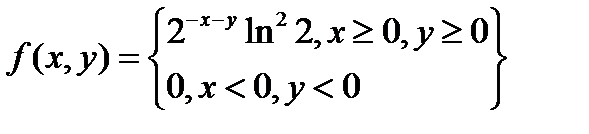
б) Для нахождения вероятности попадания случайной точки (X,Y) в треугольник с вершинами A(1;3), B(3;3), C(2;8), используем формулу: 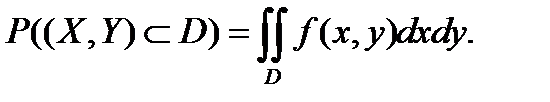
Сначала рассмотрим область D, изображенную на рисунке ниже. Как видно из рисунка, область D представляет собой треугольник ABC. Рассмотрим треугольник ABC. Будем вычислять интеграл при условии, что область D заключена между прямыми CB и СA, если 3  y
y  8.
8.

AC: 
CB: 
Тогда искомая вероятность выражается через интеграл:
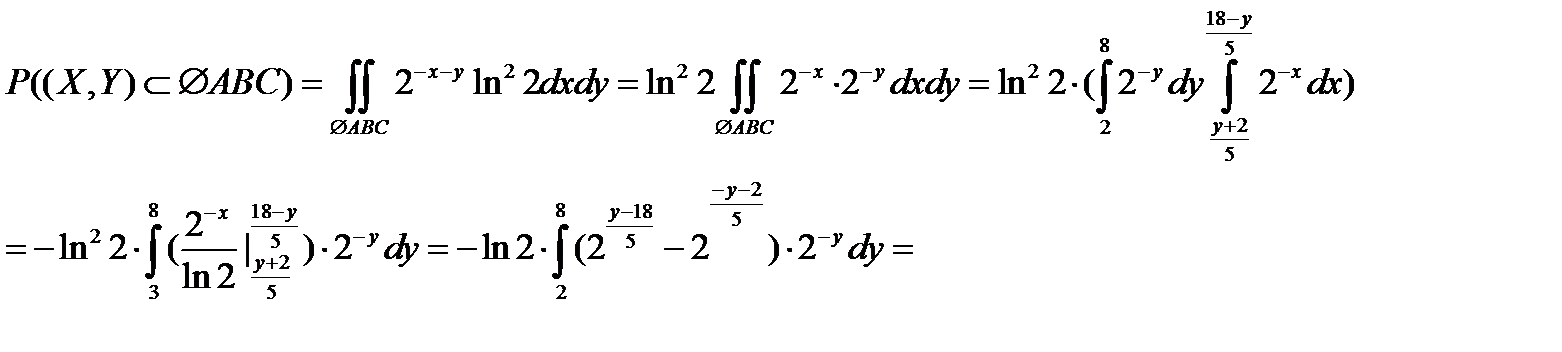

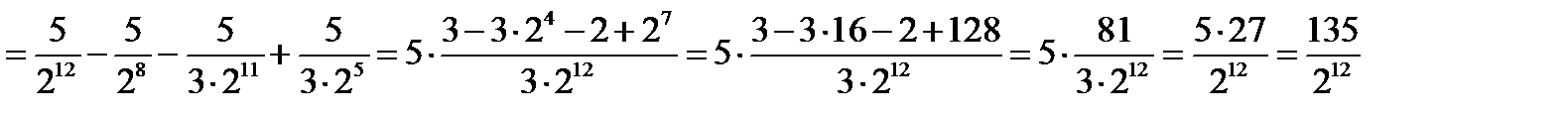
Таким образом, искомая вероятность 
Ответ: 
№421 Задана дискретная двумерная случайная величина (X,Y):
| Y | X | ||

| 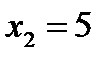
| 
| |

| 0,15 | 0,30 | 0,35 |

| 0,05 | 0,12 | 0,03 |






