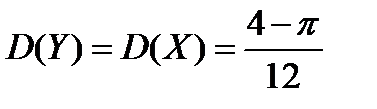Найти: а) безусловные законы распределения составляющих; б) условный закон
распределения составляющей X при условии, что составляющая Y приняла значение 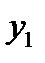 =0,4;
=0,4;
в) условный закон распределения Y при условии, что 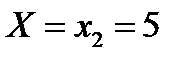
Решение:
а) Сложив вероятности «по столбцам», напишем закон распределения X:
X 2 5 8
p 0,2 0,42 0,38
Сложив вероятности «по строкам», найдем закон распределения y:
y 0,4 0,8
p 0,80 0,20
б) Найдем условные вероятности возможных значений X при условии, что составляющая Y приняла значение 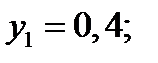
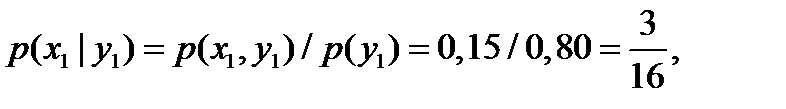
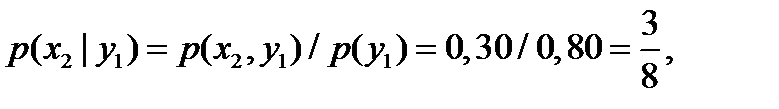

Напишем искомый условный закон распределения X:
X 2 5 8
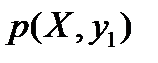
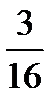
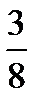
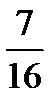
Контроль: 
в) Аналогично найдем условный закон распределения Y:
Y 0,4 0,8
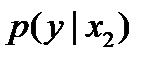
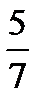
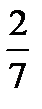
Контроль: 
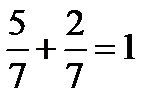 .
.
№422 Задана дискретная двумерная случайная величина (X;Y):
| Y | X | |
| 0,25 0,15 0,32 | 0,10 0,05 0,13 |
Найти: а) условный закон распределения X при условии, что Y=10; б) условный закон распределения Y при условии, что X=6.
Решение:
а) Найдем условные вероятности возможных X при условии, что составляющая Y приняла значение 10:

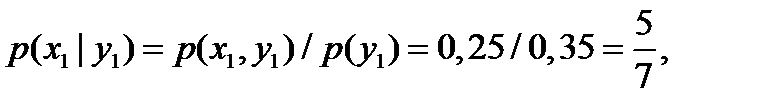
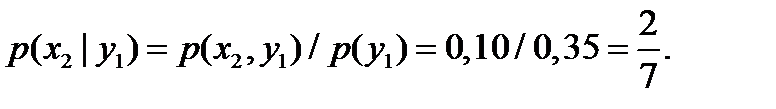
Напишем искомый условный закон распределения X:
X 3 6
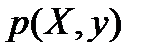
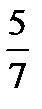
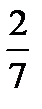
Контроль: 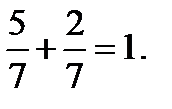
б) Аналогично найдем условный закон распределения Y:
Y 10 14 18
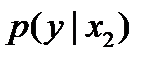

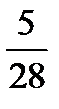
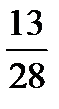
Контроль: 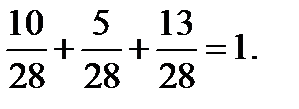
№423 Задана плотность совместного распределения непрерывной двумерной случайной
величины (X,Y):
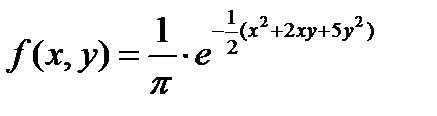
Найти: а) плотности распределения составляющих; б) условные плотности
распределения составляющих.
Решение: а) Найдем плотность распределения составляющей X:
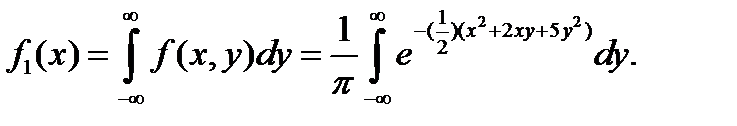
Вынесем за знак интеграла множитель  , не зависящий от переменной интегрирования y, и дополним оставшийся показатель степени до полного квадрата; тогда
, не зависящий от переменной интегрирования y, и дополним оставшийся показатель степени до полного квадрата; тогда
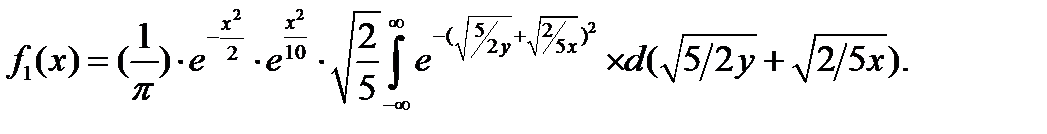
Учитывая, что интеграл Пуассона  , окончательно получим плотность распределения составляющей X:
, окончательно получим плотность распределения составляющей X:

Аналогично найдем плотность распределения составляющей Y:
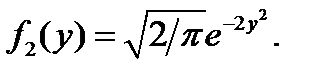
б) Найдем условные плотности распределения составляющих. Выполнив элементарные выкладки, получим:
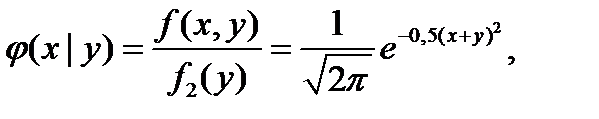
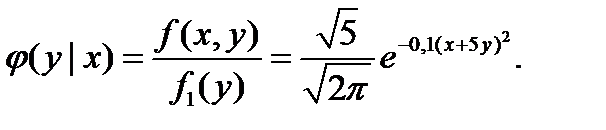
№424 Плотность совместного распределения непрерывной двумерной случайной величины (X,Y):
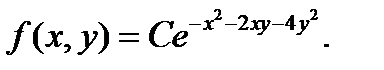
Найти: а) постоянный множитель C; б) плотности распределения составляющих; в)
условные плотности распределения составляющих.
Решение:
а) Воспользуемся свойством двумерной плотности распределения: 
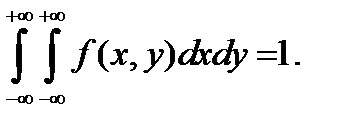
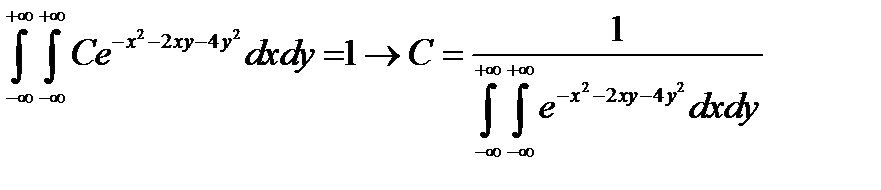
Вычислим интеграл:
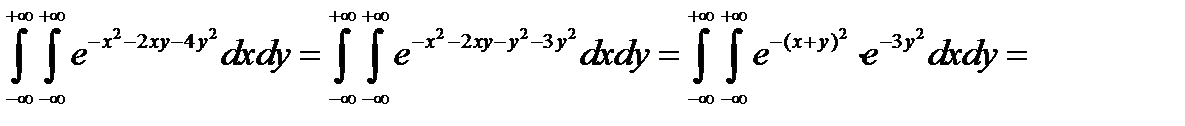
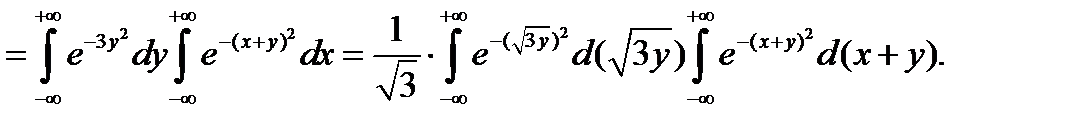
Учитывая, что интеграл Пуассона 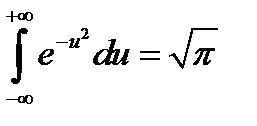 , окончательно получи
, окончательно получи

Тогда постоянная 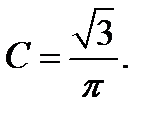
б) Найдем плотность распределения составляющей X:
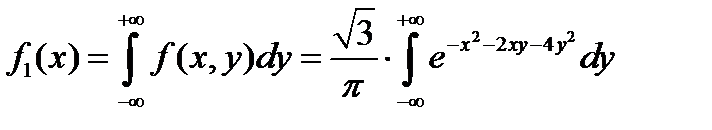
Вынесем за знак интеграла множитель 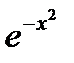 , не зависящий от переменной интегрирования y, и дополним оставшийся показатель степени до полного квадрата, тогда:
, не зависящий от переменной интегрирования y, и дополним оставшийся показатель степени до полного квадрата, тогда:
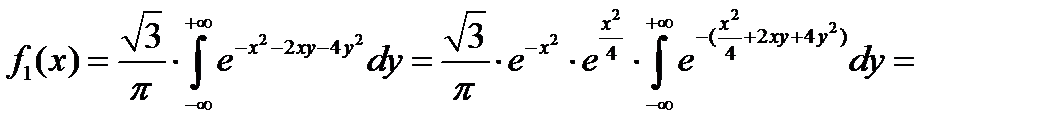
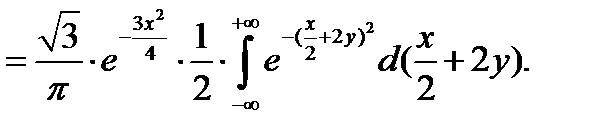
Учитывая, что интеграл Пуассона 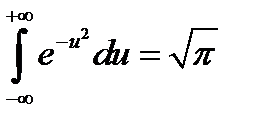 , окончательно получим плотность распределения составляющей X:
, окончательно получим плотность распределения составляющей X:
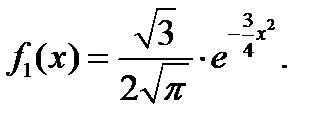
Найдем плотность распределения составляющей Y:
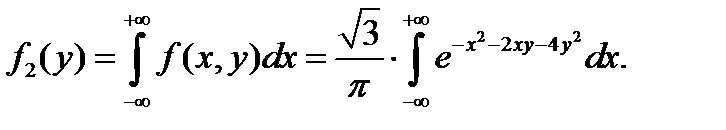
Вынесем за знак интеграла множитель 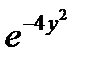 , не зависящий от переменной интегрирования x, и дополним оставшийся показатель степени до полного квадрата, тогда:
, не зависящий от переменной интегрирования x, и дополним оставшийся показатель степени до полного квадрата, тогда:
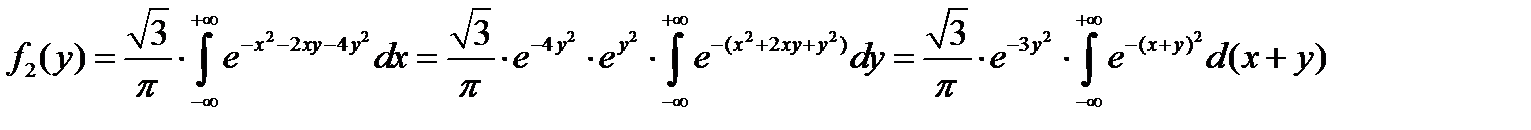 Учитывая, что интеграл Пуассона
Учитывая, что интеграл Пуассона 
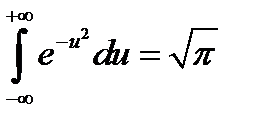 , окончательно получим плотность распределения составляющей Y:
, окончательно получим плотность распределения составляющей Y:
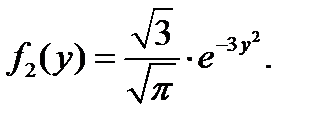
в) Найдем условные плотности распределения составляющих выполнив элементарные выкладкт, получим:
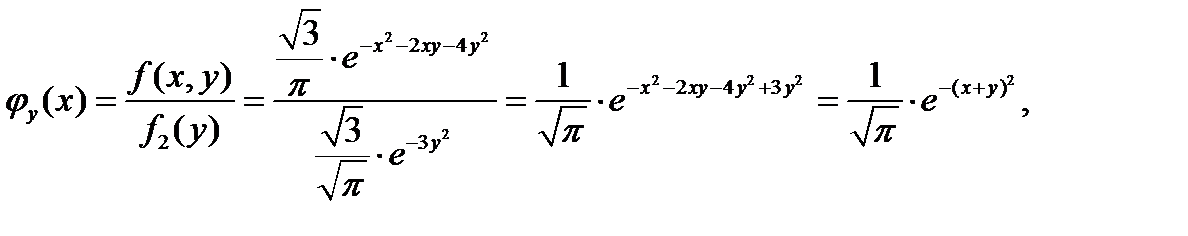
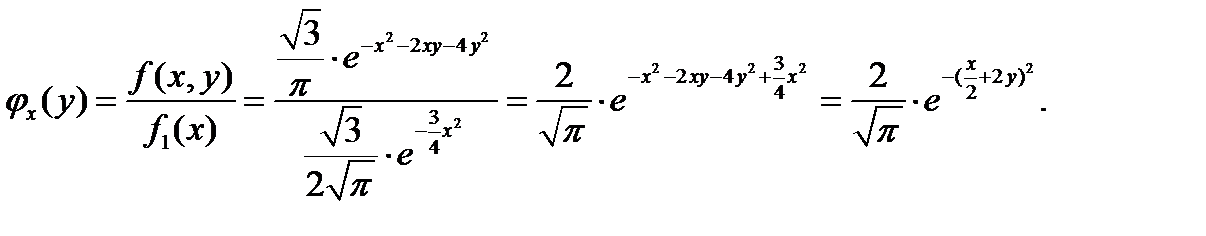
Таким образом, 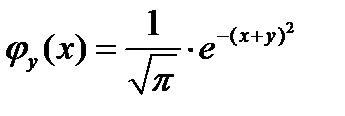 и
и 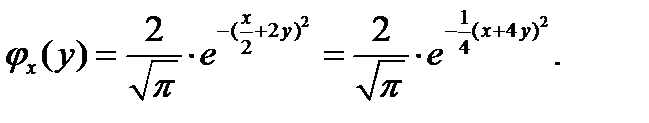
№425 Плотность совместного распределения непрерывной двумерной случайной величины
 в квадрате 0≤x≤π/2, 0≤y≤π/2; вне квадрата
в квадрате 0≤x≤π/2, 0≤y≤π/2; вне квадрата 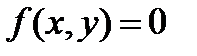 . Доказать, что
. Доказать, что
составляющие X и Y независимы.
Решение:
Найдем плотность распределения составляющей X:
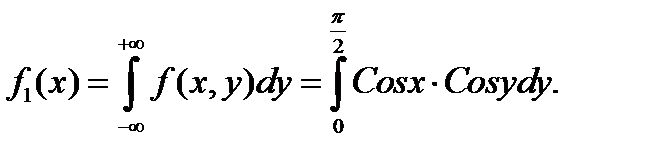
Вынесем за знак интеграла множитель 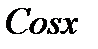 , не зависящий от переменной интегрирования y, тогда:
, не зависящий от переменной интегрирования y, тогда:
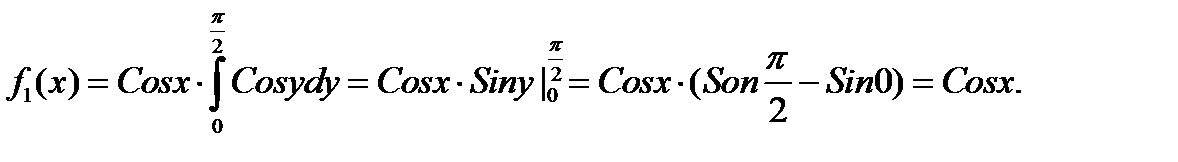
Найдем плотность распределения составляющей Y:
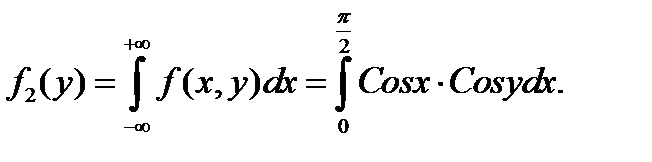
Вынесем за знак интеграла множитель 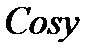 , не зависящий от переменной интегрирования x, тогда:
, не зависящий от переменной интегрирования x, тогда:
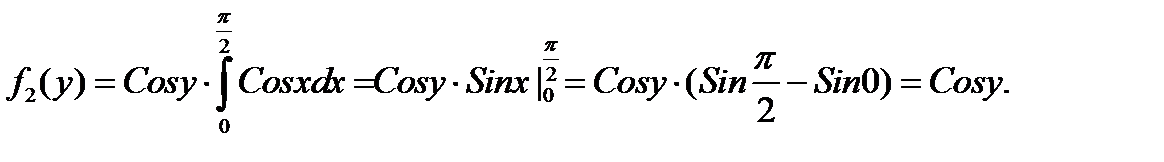
Найдем условные плотности распределения составляющих:
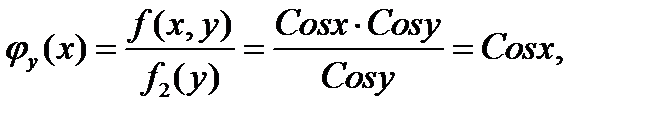

Получаем, 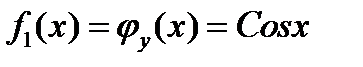 и
и 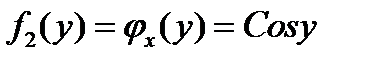 . Другими словами условные плотности распределения случайных величин X и Y равны их безусловным плотностям, а это значит, что эти величины независимы.
. Другими словами условные плотности распределения случайных величин X и Y равны их безусловным плотностям, а это значит, что эти величины независимы.
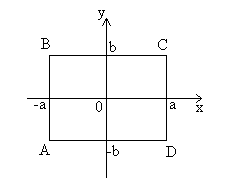
№426 Непрерывная двумерная случайная величина (X,Y) распределена равномерно внутри
прямоугольника с центром симметрии в начале координат и сторонами 2а и 2b,
параллельными координатным осям. Найти: а) двумерную плотность вероятности системы;
б) плотности распределения составляющих.
Решение:
а) Поскольку распределение равномерное, то 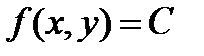 . Воспользуемся свойством плотности вероятности:
. Воспользуемся свойством плотности вероятности:
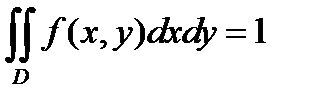
Для нашей области D, которая представляет собой прямоугольник ABCD, получим:
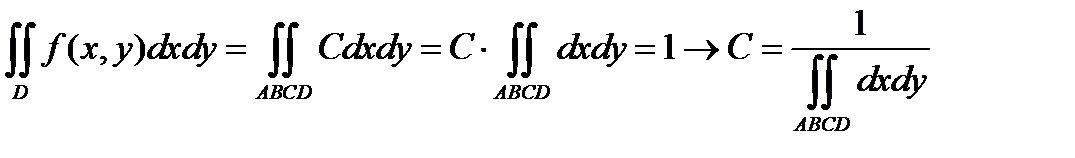
Вычислим интеграл: 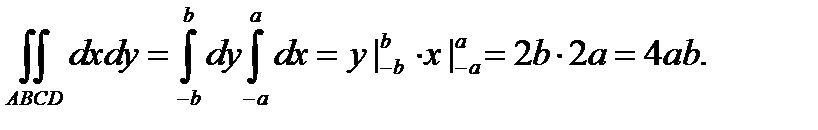
Тогда 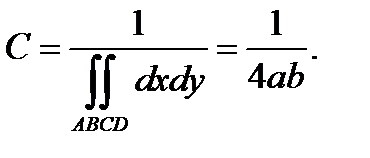
Двумерная плотность вероятности имеет вид: 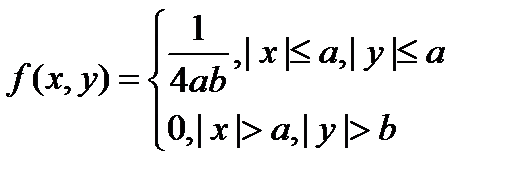
б) Найдем плотность составляющей X:
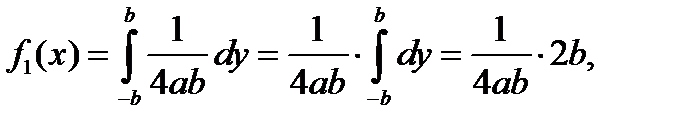 т.е
т.е 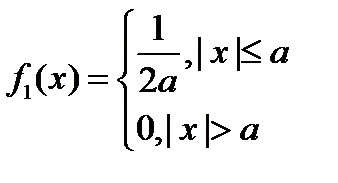
Найдем плотность составляющей Y:
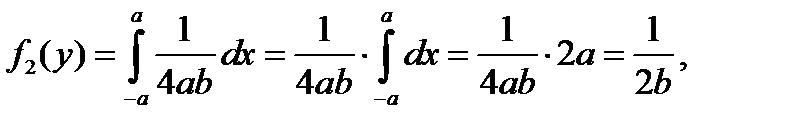 т.е.
т.е. 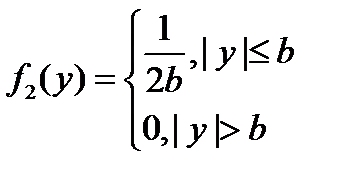
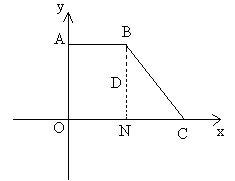
№427 Непрерывная двумерная случайная величина (X,Y) распределена равномерно внутри
прямоугольной трапеции с вершинами O(0;0), A(0;4), B(3;4), С(6;0). Найти: а) двумерную
плотность вероятности системы; б) плотности распределения составляющих.
Решение:
а) Поскольку распределение равномерное, то 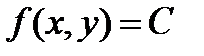 . Воспользуемся свойством
. Воспользуемся свойством
плотности вероятности:
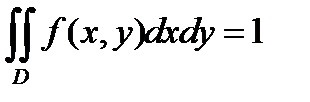
Для нашей области D, которая представляет собой трапецию OABC, получим:

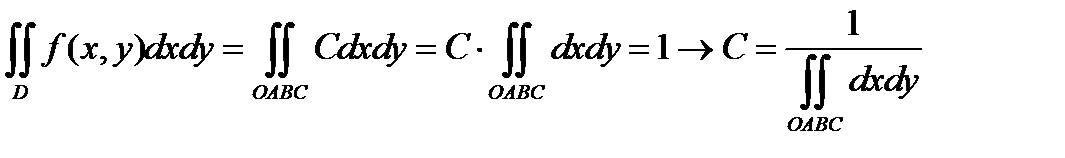
Область D разобьем на две области D1 - прямоугольник OABN и D2 - прямоугольный
треугольник NBC. Рассмотрим эти области.
Область D1 – прямоугольник OABN сверху ограничен прямой AB, уравнение которой
y=4, а снизу - прямой ON, уравнение которой y=0, при этом 0≤x≤3.
Область D2 – прямоугольный треугольник NBC сверху ограничен прямой BC, а снизу -
прямой NC, уравнение которой y=0, при этом 3≤x≤6.
Найдем уравнение прямой NC: 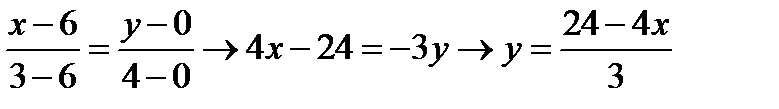
Вычислим интеграл:
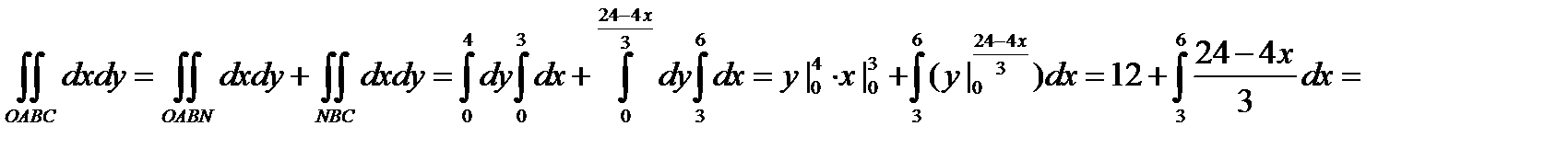
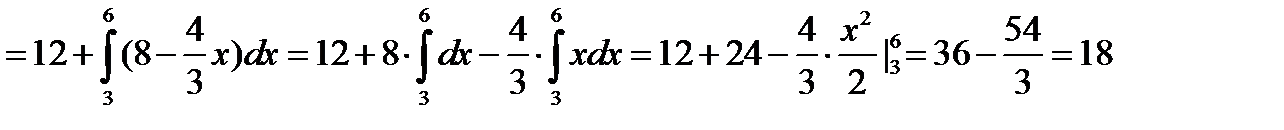
Тогда 
Двумерная плотность вероятности имеет вид: 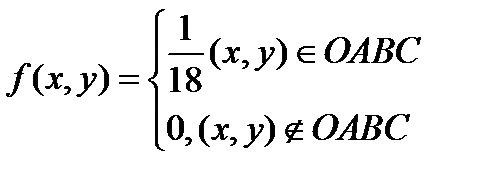
б) Найдем плотность составляющей X:
Если x<0, то 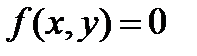 , тогда
, тогда 
Если 0<x<3, то 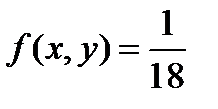 , тогда
, тогда 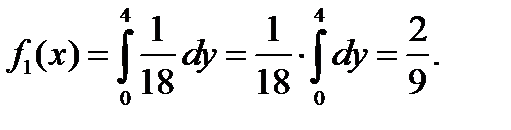
Если 3<x<6, то 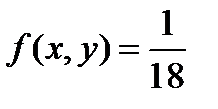 , тогда
, тогда 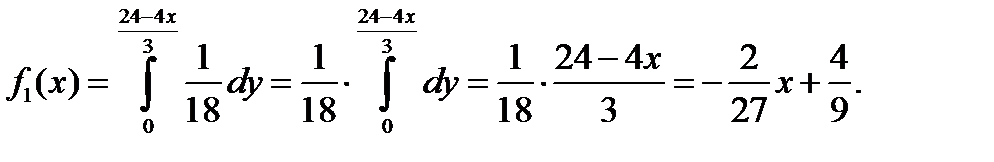
Если x>6, то 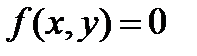 , тогда
, тогда 
Таким образом, плотность вероятности составляющей X:
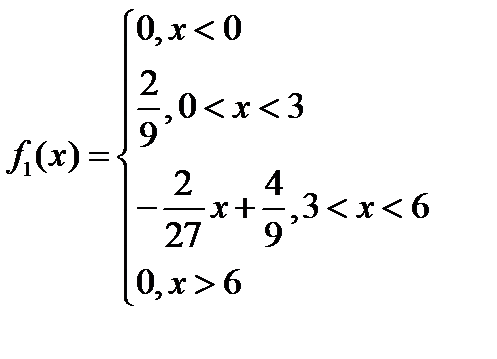
Найдем плотность составляющей Y:
Если y<0, y>4, то 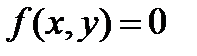 , тогда
, тогда 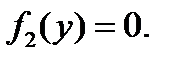
Если 0<y<4, то 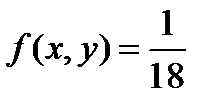 , область ограничена сверху прямой BC, уравнение которой
, область ограничена сверху прямой BC, уравнение которой 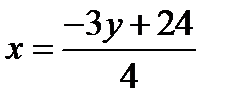 , а снизу прямой
, а снизу прямой 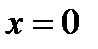 , тогда:
, тогда:
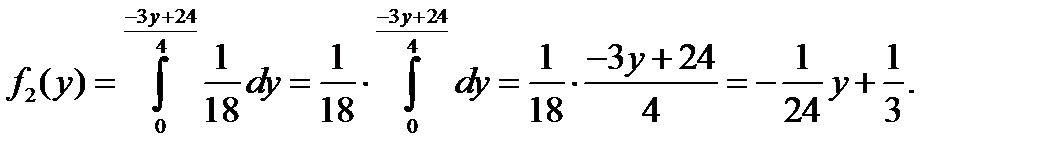
№428 Непрерывная двумерная случайная величина (X,Y) равномерно распределена внутри прямоугольного треугольника с вершинами O(0;0), A(0;8), B(8;0). Найти: а) двумерную плотность вероятности системы; б) плотности и условные плотности распределения составляющих.
Решение:
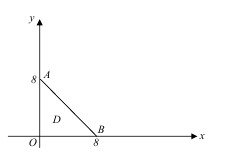
а) Поскольку случайная величина распределена равномерно, то обозначим плотность совместного распределения через C, т.е. 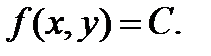 Область интегрирования D – есть прямоугольный треугольник OAB.
Область интегрирования D – есть прямоугольный треугольник OAB.
Воспользуемся свойством двумерной плотности распределения: 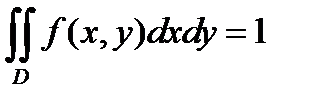
Для нашего случая получаем:
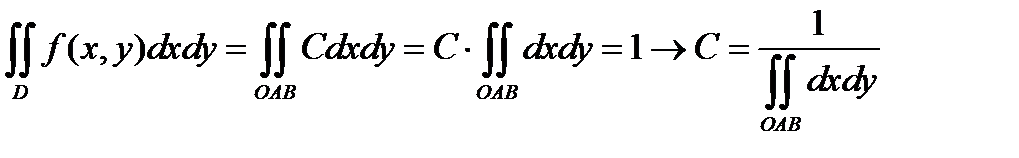
Рассмотрим треугольник OAB=D. Сверху треугольник ограничен прямой AB, а снизу – прямой OB, уравнение которой y=0, при этом 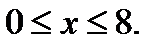
Найдем уравнение прямой AB: 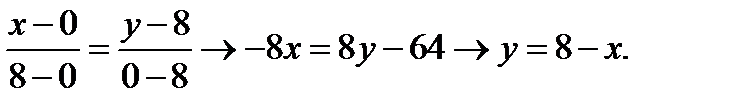
Вычислим интеграл:

Тогда совместная плотность вероятности 
б) Найдем плотность распределения составляющей X:
Если 0<x<8, то 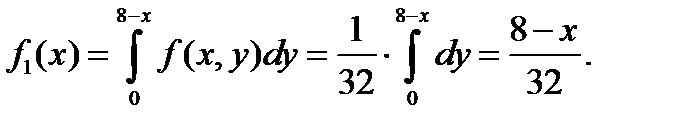
Таким образом, плотность распределения вид: 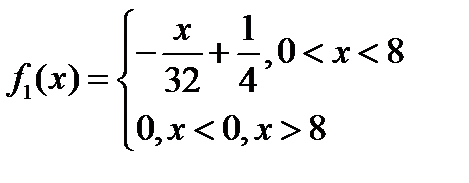
Найдем плотность распределения составляющей Y:
Если 0<y<8, то 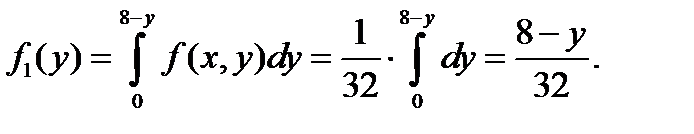
Таким образом, плотность распределения вид: 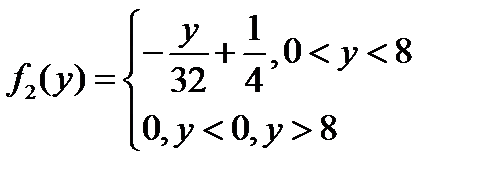
Найдем условные плотности распределения составляющих. Выполнив элементарные выкладки, получим:
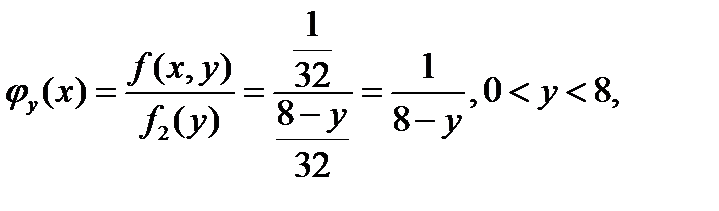
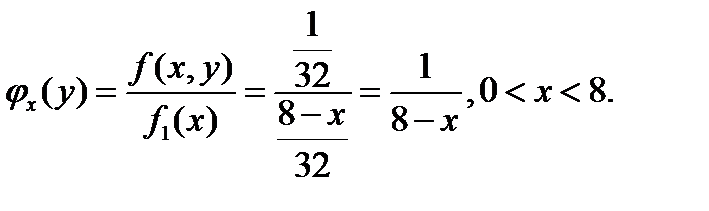
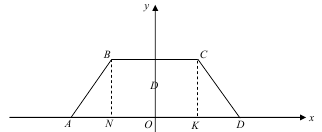
№429 Непрерывная двумерная случайная величина (X,Y) равномерно распределена внутри трапеции с вершинами A(-6;0), B(-3;4), C(3;4), D(6;0),. Найти: а) двумерную плотность вероятности системы; б) плотности распределения составляющих.
Решение:
Поскольку случайная величина распределена равномерно, то обозначим плотность
совместного распределения через C, т.е. 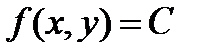 . Область интегрирования D – есть
. Область интегрирования D – есть
трапеция ABCD.
Воспользуемся свойством двумерной плотности распределения: 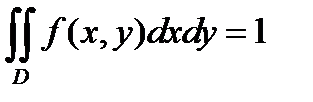
Для нашего случая получаем: 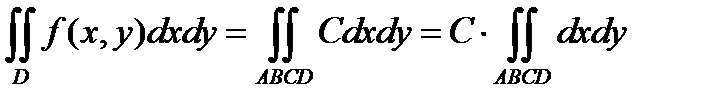
Рассмотрим трапецию ABCD - область D. Разобьем область D, на три части:
прямоугольный треугольник ABN, прямоугольник NBCK и прямоугольный треугольник KCD.
Рассмотрим треугольник ABN. Сверху треугольник ограничен прямой AB, а снизу -
прямой ON, уравнение которой y=0, при этом -6< x<-3.
Найдем уравнение прямой AB: 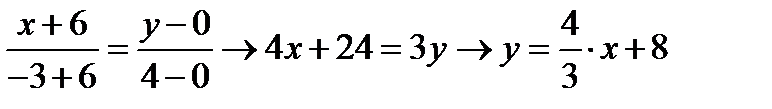
Рассмотрим прямоугольник NBCK. Сверху прямоугольник ограничен прямой BC, уравнение которой y=4, а снизу - прямой ON, уравнение которой y=0, при этом -3<x<3.
Рассмотрим треугольник ABN. Сверху треугольник ограничен прямой AB, а снизу -
прямой ON, уравнение которой y=0, при этом 3<x<6.
Найдем уравнение прямой CD: 
Вычислим интеграл:
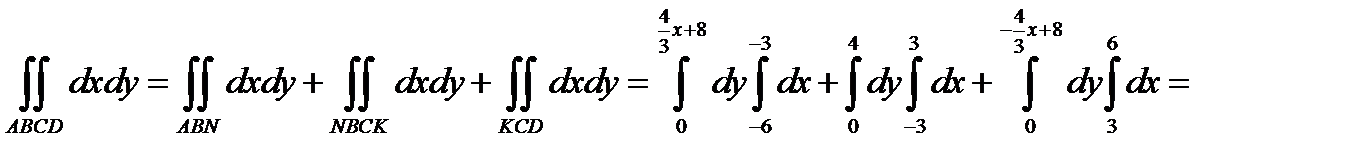

Тогда совместная плотность вероятности 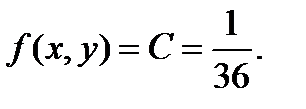
б) Найдем плотность распределения составляющей X:
Если x<-6, то f(x,y)=0, следовательно, f1(x)=0
Если -6<x<-3, то 
Если -3<x<3, то 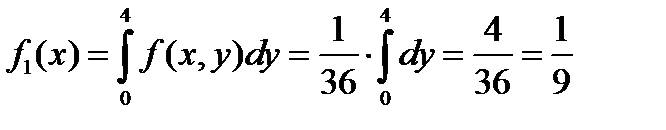
Если 3<x<6, то  .
.
Если x<6, то f(x,y)=0, следовательно 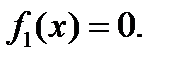
Таким образом, плотность распределения X имеет вид: 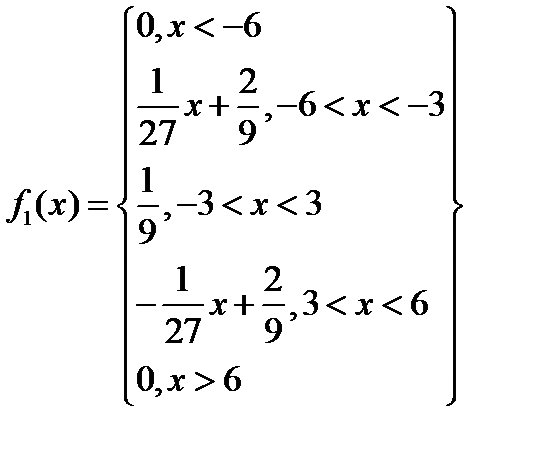
Найдем плотность распределения составляющей Y:
Если 0<y<4, то трапеция ABCD сверху ограничена прямой CD, уравнение которой 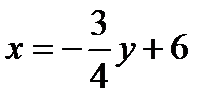 , а снизу - прямой AB, уравнение которой
, а снизу - прямой AB, уравнение которой 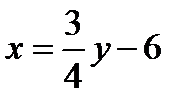 .
.
Если 0<y<4,то 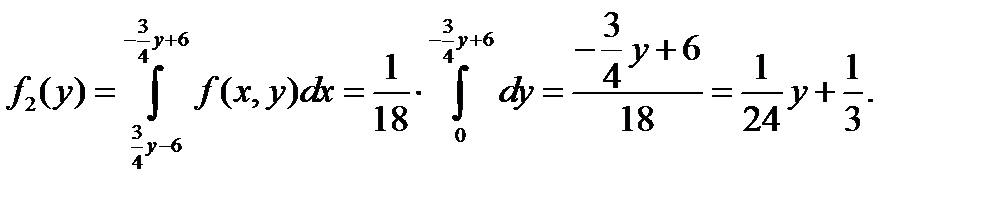
Таким образом, плотность распределения Y имеет вид:  .
.
№430. Задана плотность совместного распределения двумерной случайной величины (X,Y):
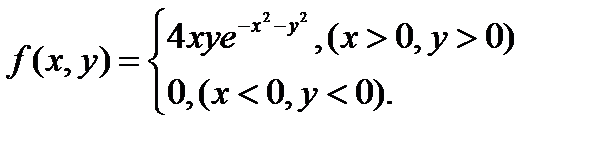
Найти: а) математические ожидания; б) дисперсии составляющих X и Y.
Решение:
а) Найдем сначала плотность распределения составляющей X:
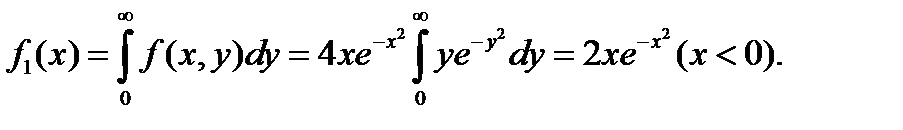
Аналогично получим
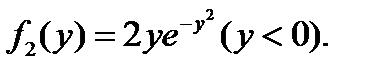
Найдем математическое ожидание составляющей X:
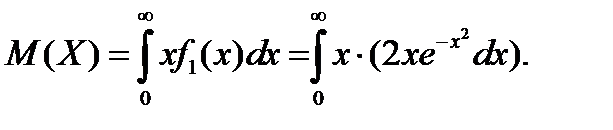
Интегрируя по частям и учитывая, что интеграл Пуассона 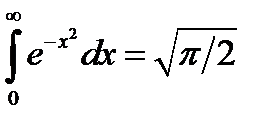 , получим
, получим 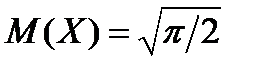 . Очевидно, что
. Очевидно, что 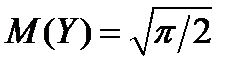 .
.
б) Найдем дисперсию X:
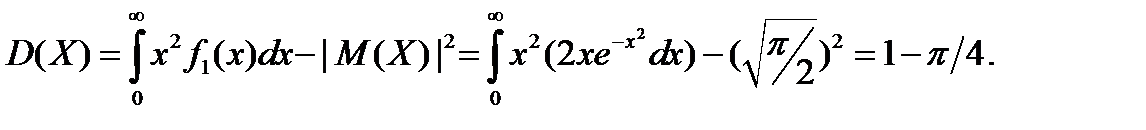
Очевидно, что 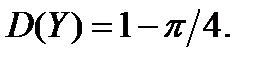
Прокаева Наталия
№431 Задана плотность совместного распределения двумерной случайной величины (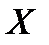 ,
,  )
) 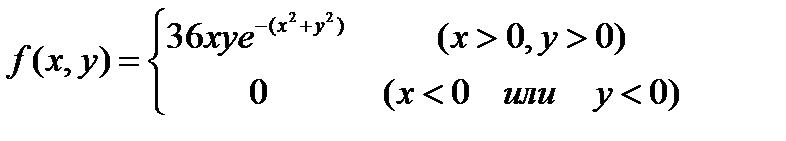
Найти математические ожидания и дисперсии составляющих.
Решение:
Найдем сначала плотность распределения составляющей  :
:
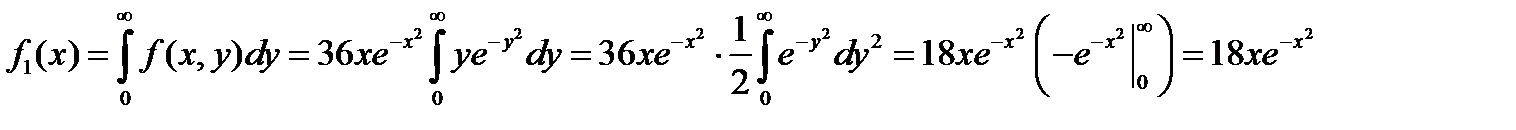 (
(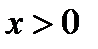 ).
).
Аналогично получим
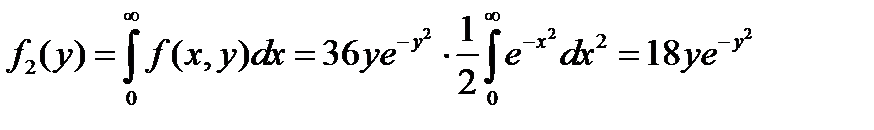 (
(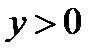 ).
).
Найдем математическое ожидание составляющей 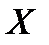 :
:
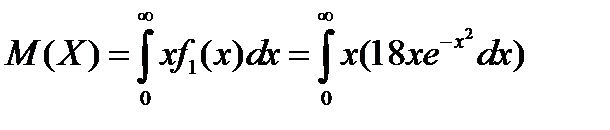
Учитывая, что интеграл Пуассона 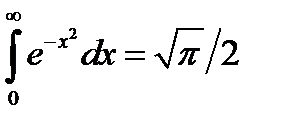 , получим
, получим
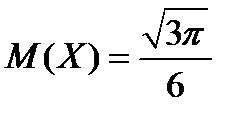 . Очевидно, что
. Очевидно, что 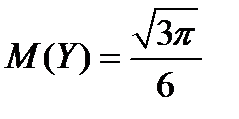 .
.
Найдем дисперсию 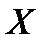 :
:
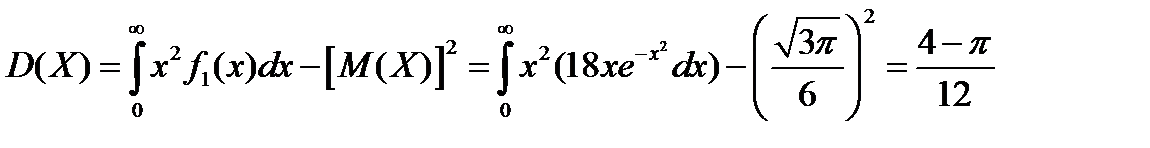
Очевидно, что 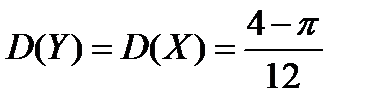
Ответ: 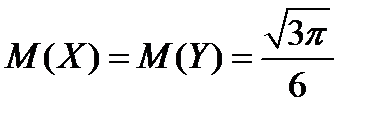 ;
;