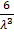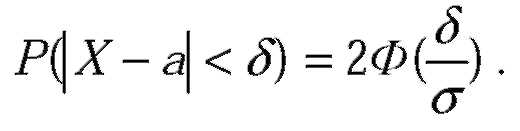
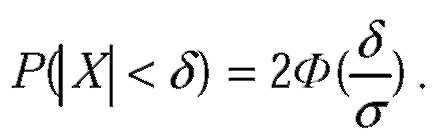
|
|
| В частности, если a=0, то справедливо равенство: |
|
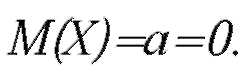
| Воспользуемся |
| X - отклонение (размера детали от проектного размера), |
|
|
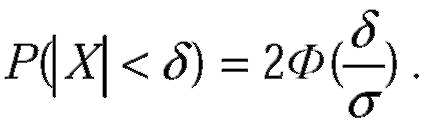
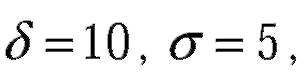
| получим: |
| формулой: |
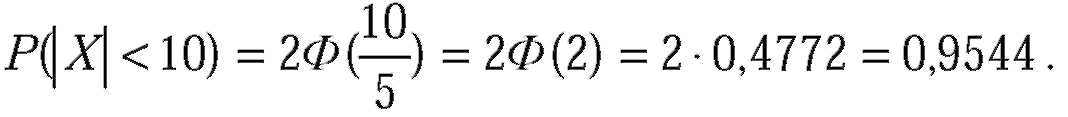
| Подставив |
| Таким образом, вероятность отклонения размера, меньшего 10мм, равна 0,9544. Отсюда следует, что примерно 95,44% деталей из общего числа, производимого автоматом, окажутся годными. |
| № 336Бомбардировщик, пролетевший вдоль моста, длина которого 30м и ширина 8м, сбросил бомбы. Случайные величины X и Y (расстояния от вертикальной и горизонтальной осей симметрии моста до места падения бомбы) независимы и, распределены нормально со среднеквадратическими отклонениями, соответственно равными 6 и 4м, и математическими ожиданиями, равными нулю. Найти: а) вероятность попадания в мост одной сброшенной бомбы; б) вероятность разрушения моста, если сброшены две бомбы, причем известно, что для разрушения моста достаточно одного попадания. |
|
| , равна: |
|
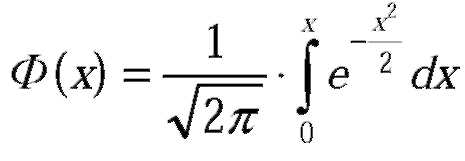
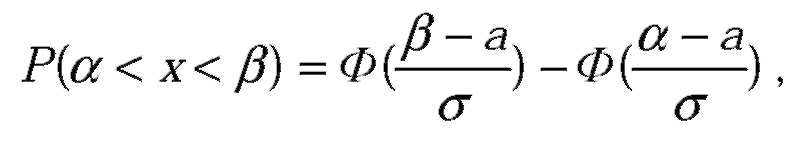
| Вероятность того, что X примет значение, принадлежащее интервалу |
| - функция Лапласа. |
| где |
| Вероятность того, что абсолютная величина отклонения меньше положительного числа |
|
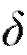
| , равна: |
|
|
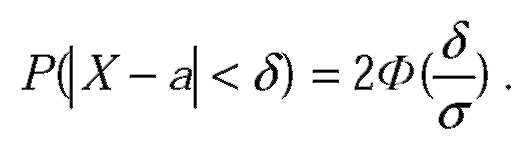
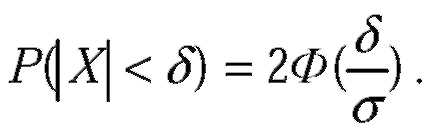
| В частности, если a=0, то справедливо равенство: |
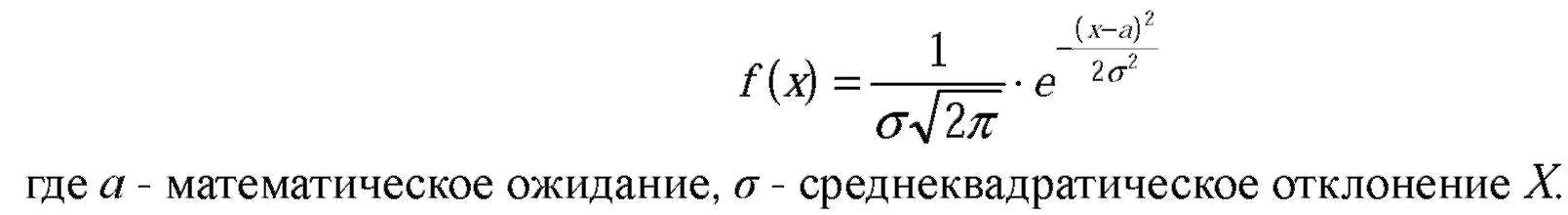
| Решение: Нормальным называют распределение вероятностей непрерывной случайной величины X, плотность которого имеет вид: |
|
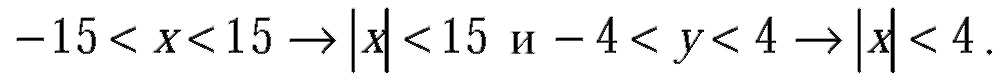
| а) Поскольку случайные величины X и Y - расстояния от вертикальной и горизонтальной осей симметрии моста до места падения бомбы, то в случае попадания бомбы x заключено в интервале (-15,15) - измерение расстояния по длине моста от центра, y - в интервале (-4,4) - измерение расстояния по ширине моста от центра. Таким образом, при попадании одновременно должны выполниться два условия: |
|
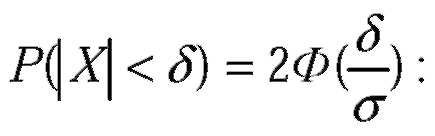
| Вычислим вероятности этих условий по формуле |
|
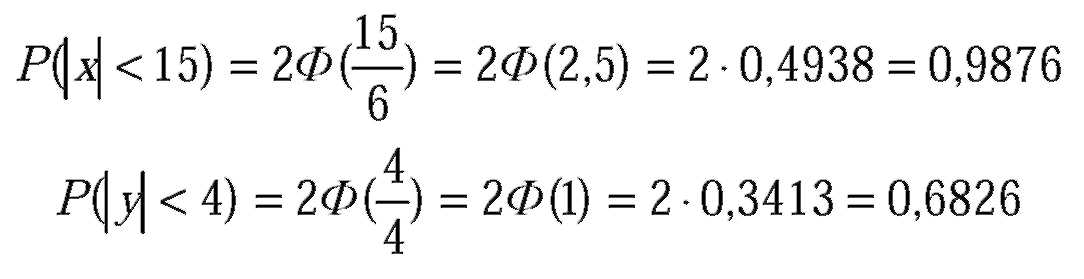
| Поскольку величины X и Y - независимы, то вероятность произведения равна |
| произведению вероятностей, т.е. |
|
|
| Таким образом, вероятность попадания бомбы при одном сбрасывании равна 0,6741. |
| б) Рассмотрим случай, когда сброшены две бомбы. Событие А - мост будет разрушен, когда попадет одна бомба или обе сброшенные бомбы. Вероятность разрушения моста можно найти, если рассмотреть противоположное событие - ни одна из двух бомб не попадет. Если вероятность попадания при одном сбрасывании равна p = 0,6741, то вероятность промаха равна q = 1 - p = 1 - 0,6741 = 0,3259. Тогда вероятность того, что ни одна из двух сброшенных бомб не попадет, равна: |
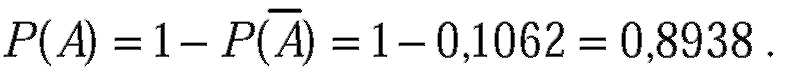
| Тогда вероятность, что мост будет разрушен, если на него сброшены две бомбы, равна: |
Борисов Александр
№337 Случайная величина X распределена нормально с математическим ожиданием a=10. Вероятность попадания X в интервал (10,20) равно 0.3. Чему равна вероятность попадания X в интервал (0,10)?
Решение:
Так как нормальная кривая симметрична относительно прямой x=a=10, то площади, ограниченные сверху нормальной кривой и снизу – интервалами (0,10) и (10,20), равны между собой. Поскольку эти площади численно равны вероятностям попадания X в соответствующий интервал, то:
P(0<X<10)=P(10<X<20)=0.3
Ответ: 0.3
№338 Случайная величина X распределена нормально с математическим ожиданием a=25. Вероятность попадания X в интервал (10,15) равно 0.3. Чему равна вероятность попадания X в интервал (35,40)?
Решение:
Так как нормальная кривая симметрична относительно прямой x=a=25, то площади, ограниченные сверху нормальной кривой и снизу – интервалами (10,15) и (35,40), равны между собой. Поскольку эти площади численно равны вероятностям попадания X в соответствующий интервал, то:
P(10<X<15)=P(35<X<40)=0.2
Ответ: 0.2
№339 Доказать, что:
т.е. что значение удвоенной функции Лапласа при заданном t определяет вероятность того, что отклонение X-a нормально распределенной величины X по абсолютной величине меньше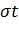 
.
Решение:
Используем формулу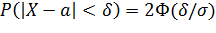 
Сделаем замену: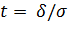 
=> 
В итоге получаем требуемую формулу:
Ч.Т.Д.
№340 Вывести «Правило трех сигм»: вероятность того, что абсолютная величина отклонения нормально распределенной случайной величины будет меньше утроенного среднего квадратического отклонения, равна 0.9973.
Решение:
Воспользуемся формулой, которая доказывается в номере №339, а именно:
Положим t=3, тогда:
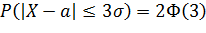
По таблице, которая находится в конце задачника, определяем, чему равна 
.
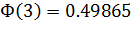, тогда 
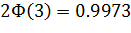, а значит:
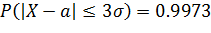
Ч.Т.Д.
№341 Случайная величина X распределена нормально с математическим ожиданием a=10 и средним квадратическим отклонением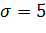 
. Найти интервал, симметричный относительно математического ожидания, в который с вероятностью 0.9973 попадает величина X в результате испытания.
Решения:
Зная, что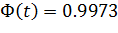 
, по таблице значений формулы Лапласа находим, что t=3.
Подставляем все имеющиеся у нас значения в формулу:
И получаем:
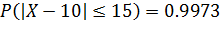
Решаем неравенство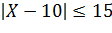 
и получаем:
Ответ: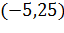 
№342 Случайная величина X распределена нормально со средним квадратическим отклонением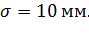 
Найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 0,9973 попадет X в результате испытания.
Решение:
Зная, что 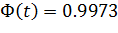, по таблице значений формулы Лапласа находим, что t=3.
Подставляем все имеющиеся у нас значения в формулу:
И получаем:
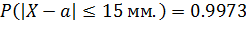
Очевидно, что если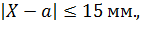 
то длинна интервала будет равна 30 мм.
Ответ: 30 мм.
№343 Станок-автомат изготовляет валики, причем контролирует их диаметр X. Считая, что X – нормально распределенная случайная величина X с математическим ожиданием a=10 мм. и средним квадаратическим отклонением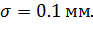 
Найти интервал, симметричный относительно математического ожидания, в которое с вероятностью 0.9973 будут заключены диаметры изготовленных валиков.
Решение:
Будем использовать формулу:
По таблице, которая приводится в конце учебника, находим, что если 
, то t=3.
Искомый интервал находится из неравенства: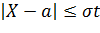 
Подставляя имеющиеся у нас значения, получаем: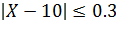 
Решаем данное неравенство, и получаем искомый интервал:
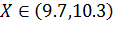
Ответ: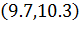 
№344 Нормально распределенная величина X задана плотностью
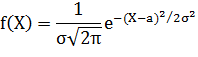
Найти моду и медиану X.
Решение:
Модой Mo(X) называют то возможное значение X, при котором плотность распределения имеет максимум. Легко убедится, что при X=a производная
f ’(a)=0; при X<a производная f ’(a)>0, при X>a производная f ’(a)>0; таким образом, точка X=a есть точка максимума, следовательно, Mo(X)=a
Медианой Me(X) называют то возможное значение X, при котором ордината f(X) делит пополам площадь, ограниченную кривой распределения. Так как нормальная кривая (график функции f(X)) симметрична относительно прямой X=a, то ордината f(a) делит пополам площадь, ограниченную нормальной кривой. Следовательно, Me(X)=a.
Итак, мода и медиана нормального распределения совпадают с математическим ожиданием.
№345 Случайная величина X распределена нормально, причем математическое ожидание a=0 и среднее квадратическое отклонение равно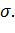 
Найти значение 
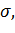при котором вероятность того, что X примет значения, принадлежащее интервалу (
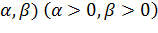будет наибольшей.
Решение:
Воспользуемся формулой: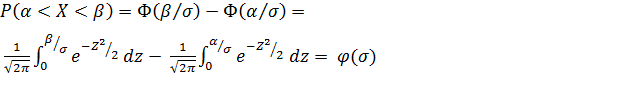 
Зная, что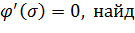 
ем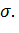 
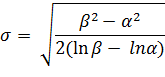
Ответ: 
№346 Написать плотность и функцию распределения показательного закон, если параметр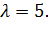 
Решение:
Подставив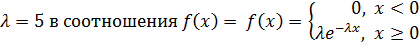 
и
F(x) =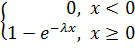 
Получаем:
F(x) =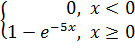 
№347 Написать плотность и функцию распределения показательного закона, если параметр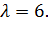 
Решение:
Подставив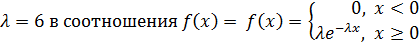 
и
F(x) =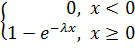
Получаем:
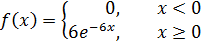
F(x) =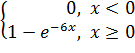 
№348 Найти параметр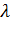 
показательного распределения: a) заданного плотностью f(x)=0 при x<0, 
при x 
б) заданного функцией распределения F(x)=0 при x<0 и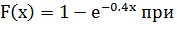 
x 
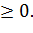
Решение:
Учитывая, что функция плотности выглядит так:
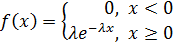, то, очевидно, что в случае плотности
, 
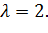
б) Учитывая, что функция распределения выглядит так:
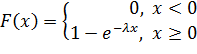, то, очевидно, что в случае плотности
, 
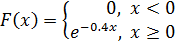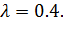
Ответ: a) 2; b) 0.4
Захаров Сергей
№ 349 Доказать, что если непрерывная случайная величина Х распределена по показательному закону, то вероятность попадания Х в интеграл (a,b) равна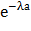 
- 
.
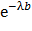Решение: Пусть величина Х задана функцией распределения F(х) = 1 -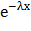 
. Тогда вероятность попадания Х в интервал (а,b).
P(a < X < b) = f(b) –f(a) = [1 -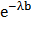 
] – [1 - 
] = -
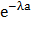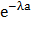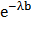
№ 350 Непрерывная случайная величина Х распределена по показательному закону, заданному плотностью вероятности f(x) = 3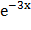 
при х ≥ 0; при х < 0 f(x) = 0.
Найти вероятность того, что в результате испытания Х попадает в интервал (0.13, 0.7)
Решение:
Используем формулу P(a < X < b) = 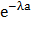- 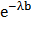. Учитывая, что, по условию, а = 0.13, b = 0.7, λ = 3, и пользуясь таблицей значений функции 
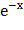, получим:
P(0.13 < X < 0.7) = 
- 
= 
- 
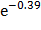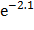= 0.677 – 0.122 = 0.555
№ 351 Непрерывная случайная величина Х распределена по показательному закону, заданному при х ≥ 0 плотностью распределения f(х) = 0.04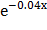 
; при х < 0 функции f(х) = 0.
Найти вероятность того, что в результате испытания Х попадает в интервал (1,2).
Решение:
По формуле P(a < X < b) = 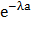- 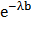(см. 350 задачу). По условию а = 1, b = 2, λ = 0.04 и пользуясь таблицей значения функции 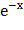, получим:
P(1 < X < 2) =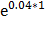 
- 
= 
- 
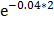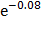
№ 352 Непрерывная случайная величина Х распределена по показательному закону, заданному функцией распределения f(х) = 1- 
; при х < 0 функции f(х) = 0.
Найти вероятность того, что в результате испытания Х попадает в интервал (2,5).
Решение:
По формуле P(a < X < b) = 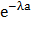- 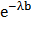(см. 350 задачу). По условию а = 2, b = 5, λ = 0.6 и пользуясь таблицей значения функции 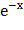, получим:
P(2 < X < 5) =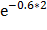 
- 
= 
- 
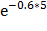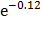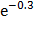
1 - -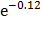
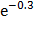
№ 353 Найти математическое ожидание показательного распределения
F(x) = λ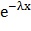 
(x ≥ 0); f(x) = 0 (x < 0).
Решение:
Используем формулу М(Х) =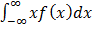 
.
Учитывая, что f(x) = 0 при х < 0 и f(x) = λ 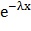при х ≥ 0, получим M(X) =λ 
.
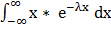Интегрируя по частям по формуле:
- 
,
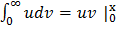Положив u =х, dv = 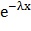dx и выполнив выкладки, окончательно получим М(Х) = 1/λ.
№ 354 Найти математическое ожидание показательного распределения, заданного при х ≥ 0:
А) плотностью f(х) = 5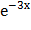 
;
Б) функцией распределения f(x) = 1 -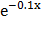 
№ 356 Найти:
А) дисперсию;
Б) среднее квадратическое отклонение показательного распределения, заданного плотностью вероятности: f(x) = λ 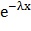при х ≥ 0; f(x) = 0 при х < 0.
Решение:
А) Используем формулу
D(X) =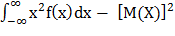 
.
Учитывая, что f(x) = 0 при х < 0, М(Х) = 1/λ получим D(x) = λ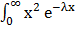 
dx – 
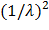
Интегрируя дважды по частям, найдем λ 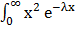dx =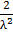 
Следовательно, искомая дисперсия
D(X) = 2/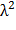 
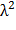– 1/ = 1/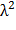
Б) найдем среднее квадратическое отклонение:
σ(Х) =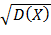 
= 1/λ
№ 357 Найти дисперсию и среднее квадратическое отклонение показательного распределения, заданного плотностью вероятности: f(x) = 10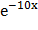 
.
Решение:
Из предыдущей задачи видим, что:
D(x) = λ 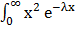dx –
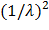
Интегрируя дважды по частям, найдем λ 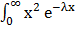dx =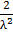
Следовательно, искомая дисперсия
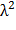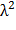D(X) = 2/ – 1/ = 1/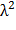
Дисперсия равна 0.01
σ(Х) = 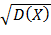= 1/λ
среднее квадратическое отклонение равна 0.1
№ 358 Найти дисперсию и среднее квадратическое отклонение показательного распределения, заданного плотностью вероятности: f(x) = 1 -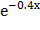 
(х ≥ 0)
Решение:
σ(х) = 
= 
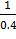= 2.5
D(x) = 
= 
= 
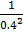= 6.25
№ 359 Студент помнит, что плотность показательного распределения имеет вид f(x) = 0 при x < 0, f(x) = C 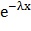при х ≥ 0; однако он забыл, чему равна постоянная С.
Требуется найти С.
Решение:
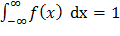
dx = 1
-λC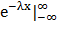 
№ 360 Найти теоретический центральный момент третьего порядка µ3= M[X – M(X)]3 показательного распределения.
Решение.
Рассмотрим центральный момент третьего порядка и сделаем преобразования, используя свойства математического ожидания: µ3= M[X – M(X)]3=M(X3- 3X2M(X) + 3XM2(X) – M3(X))= M(X3) – 3M(X2)M(X) + 3M(X)M2(X) – M3(X) = M(X3) – 3M(X2)M(X) + 2M3(X)
Подставляя М(Х)=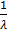 
получим µ3= M(X3) – 3M(X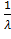2) 
+ 2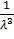 
Найдем M(X3): M(X3) =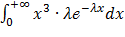 
= 
= = 
=
= 
= 
= 
= 
= = 
= 
)= 
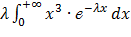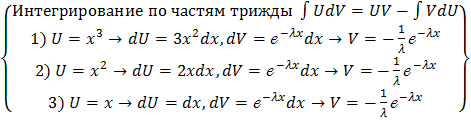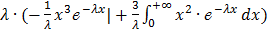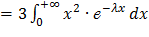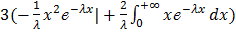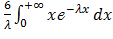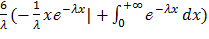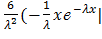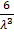
Итак, M(X3) 
=
