Найдем M(X2): M(X2) = 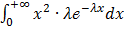 =
= 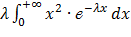 = =
= = 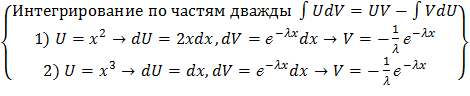 = =
= = 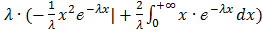 =
= 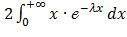 =
= 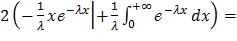 =
=  =
= 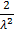
Значит, M(X2)= 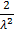
µ3= M(X3) – 3M(X2) 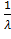 + 2
+ 2 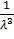 =
= 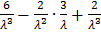 =
= 
Ответ: µ3=  .
.
Ищенко Марина
№ 361 Найти асимметрию As= µ3/σ3(X) показательного распределения.
Решение.
Рассмотрим центральный момент третьего порядка и сделаем преобразования, используя свойства математического ожидания: µ3= M[X – M(X)]3=M(X3- 3X2M(X) + 3XM2(X) – M3(X))= M(X3) – 3M(X2)M(X) + 3M(X)M2(X) – M3(X) = M(X3) – 3M(X2)M(X) + 2M3(X)
Подставляя М(Х)= 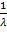 получим µ3= M(X3) – 3M(X2)
получим µ3= M(X3) – 3M(X2)  + 2
+ 2 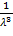
Найдем M(X3): M(X3) = 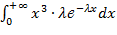 =
=  = =
= =  =
=
= 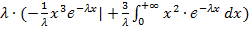 =
=  =
=  =
= 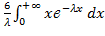 = =
= = 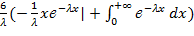 =
= 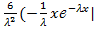 )=
)= 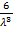
Итак, M(X3)  =
= 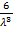
Найдем M(X2): M(X2) = 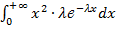 =
= 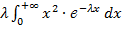 = =
= = 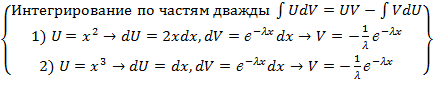 = =
= = 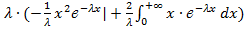 =
=  =
= 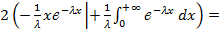 =
= 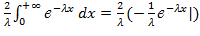 =
= 
Значит, M(X2)= 
µ3= M(X3) – 3M(X2)  + 2
+ 2 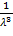 =
= 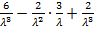 =
= 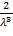
σ(X)=  (X)=
(X)= 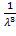
Подставим значения µ3 и 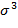 (X) в формулу As= µ3/σ3(X)
(X) в формулу As= µ3/σ3(X)
As= 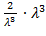 =2
=2
Ответ: 2
№ 362 Найти теоретический центральный момент четвертого порядка µ4= M[X – M(X)]4 показательного распределения.
Решение.
Рассмотрим центральный момент четвертого порядка и сделаем преобразования, используя свойства математического ожидания:
µ4= M[X – M(X)]4 = M ( )= = M (
)= = M (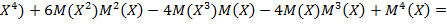 = M (
= M (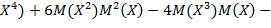 3
3 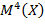
Подставляя М(Х)= 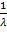 получим µ4= M (
получим µ4= M (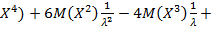

Найдем M(X4): M(X4) = 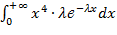 =
= 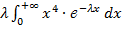 = =
= = 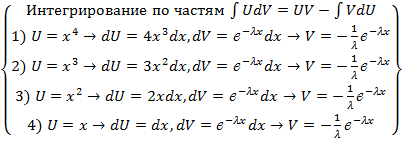 = =
= =  = 4
= 4  =
= 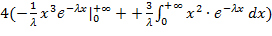 =
= 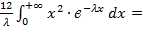
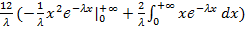 =
=  = =
= = 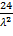
 =
= 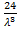
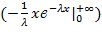 =
= 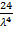
Найдем M(X3): M(X3) = 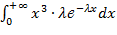 =
=  = =
= =  =
=
= 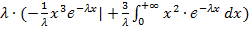 =
=  =
=  =
= 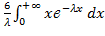 = =
= = 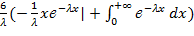 =
= 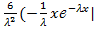 )=
)= 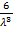
Итак, M(X3)  =
= 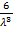
Найдем M(X2): M(X2) = 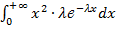 =
= 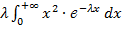 = =
= = 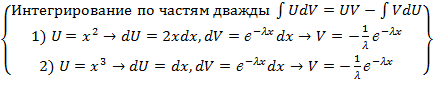 = =
= = 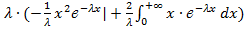 =
=  =
= 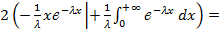 =
= 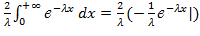 =
= 
Значит, M(X2)= 
µ4= M (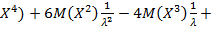
 =
= 
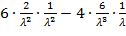 +
+  =
= 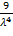
Ответ: 
№ 363 Найти эксцесс Ек= 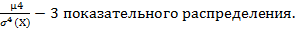
Решение.
Для решения данной задачи воспользуемся результатом вычислений задачи № 362. В задаче № 362 путем интегрирования по частям было получено µ4= 

Значит,
Ек= 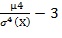 =
= 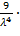
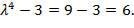
Ответ: 6.
№ 364 Доказать, что непрерывная случайная величина Т- время между появлениями двух последовательных событий простейшего потока с заданной интенсивностью λ- имеет показательное распределение F(t)= 1- 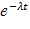 (t≥0).
(t≥0).
Решение.
Предположим, что в момент t0 наступило событие А1 потока. Пусть t1= t0+t.
Если хотя бы одно событие потока, следующее за событием А1 произойдет в интервале, заключенном внутри интервала (t0, t1), например, в интервале (t0, t2), то время Т между появлениями двух последовательных событий окажется меньше t, т.е. окажется, что Т<t.
Для того чтобы найти вероятность Р(T<t), примем во внимание, что события- “внутри интервала (t0, t1) появилось хотя бы одно событии потока” и “внутри интервала (t0, t1) не появилось ни одного события потока”- противоположны (сумма их вероятностей равна 1).
Вероятность непоявления за время t ни одного события потока Pt(0)= 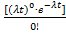 =
= 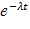 . Следовательно, интересующая нас вероятность противоположного события P(T<t)= 1-
. Следовательно, интересующая нас вероятность противоположного события P(T<t)= 1- 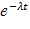 , или (по определению функции распределения F(t)= P(T<t)) имеем F(t)= 1-
, или (по определению функции распределения F(t)= P(T<t)) имеем F(t)= 1- 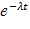 ,что и требовалось доказать.
,что и требовалось доказать.
№ 365 Задана интенсивность простейшего потока λ=5. Найти: а) математическое ожидание; б) дисперсию; в) среднее квадратическое отклонение непрерывной случаной величины Т- времени между появлениями двух последовательных событий потока.
Решение.
а) Используем формулу: М(Т)= 
Следовательно, М(Т)= 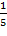 = 0,2
= 0,2
б) Используем формулу: D(T) = 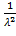
Следовательно, D(T) =  = 0,4
= 0,4
в) Используем формулу: σ(Т)= 
σ(Т)= 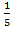 = 0,2
= 0,2
Ответ: а) 0,2; б) 0,4; в) 0,2.
№ 366 На шоссе установлен контрольный пункт для проверки технического состояния автомобилей. Найти математическое ожидание и среднее квадратическое отклонение случайной величины Т – времени ожидания очередной машины контролером, - если поток машин простейший и время (в часах) между прохождениями машин через контрольный пункт распределено по показательному закону f(t)= 5 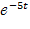 .
.
Решение.
f(t)= λ 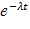 . Сле-но, λ=5.
. Сле-но, λ=5.
Воспользуемся формулой: М(t)= σ(t) = 
М(t)= σ(t)= 0,2.
Ответ: 0,2.
№ 367 Длительность времени безотказной работы элемента имеет показательное распределение F(t)=1- 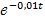 (t >0). Найти вероятность того, то за время длительностью t = 50ч: а) элемент откажет; б)элемент не откажет.
(t >0). Найти вероятность того, то за время длительностью t = 50ч: а) элемент откажет; б)элемент не откажет.
Решение.
а) Так как функция распределения F(t)=1- 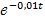 определяет вероятность отказа элемента за время длительностью t, то, подставив t=50 в функцию распределения, получим вероятность отказа:
определяет вероятность отказа элемента за время длительностью t, то, подставив t=50 в функцию распределения, получим вероятность отказа:
F(50)= 1- 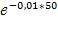 =1-
=1- 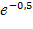 = 1- 0,606= 0,394;
= 1- 0,606= 0,394;
б) событие “элемент не откажет” получим, пользуясь функцией надежности R(t)= 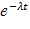 , которая определяет вероятность безотказной работы элемента за время длительность t:
, которая определяет вероятность безотказной работы элемента за время длительность t:
R(50)= 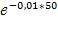 =
= 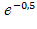 =0,606.
=0,606.
Ответ: а) 0,394; б) 0,606.
№ 368 Длительность времени безотказной работы элемента имеет показательное распределение F(t)=1- 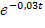 . Найти вероятность того, то за время длительностью t = 100ч: а) элемент откажет; б)элемент не откажет.
. Найти вероятность того, то за время длительностью t = 100ч: а) элемент откажет; б)элемент не откажет.
Решение.
а) Так как функция распределения F(t)=1- 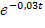 определяет вероятность отказа элемента за время длительностью t, то, подставив t=100 в функцию распределения, получим вероятность отказа:
определяет вероятность отказа элемента за время длительностью t, то, подставив t=100 в функцию распределения, получим вероятность отказа:
F(100)= 1-  =1-
=1- 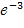 = 0,95;
= 0,95;
б) событие “элемент не откажет” получим, пользуясь функцией надежности R(t)= 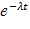 , которая определяет вероятность безотказной работы элемента за время длительность t:
, которая определяет вероятность безотказной работы элемента за время длительность t:
R(100)=  =
=  = 0,05.
= 0,05.
Ответ: а) 0,95; б) 0,05.
№ 369 Испытывают два независимо работающих элемента. Длительность времени безотказной работы первого элемента имеет показательное распределение F1(t) = 1- 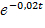 , второго F2(t) = 1-
, второго F2(t) = 1-  . Найти вероятность того, что за время длительностью t=6ч: а) оба элемента откажут; б) оба элемента не откажут; в) только один элемент откажет; г) хотя бы один элемент откажет.
. Найти вероятность того, что за время длительностью t=6ч: а) оба элемента откажут; б) оба элемента не откажут; в) только один элемент откажет; г) хотя бы один элемент откажет.
Решение.
а) Вероятность отказа первого элемента
P1=F1(6)=1- 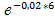 =
= 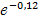 = 1- 0,887=0,113.
= 1- 0,887=0,113.
Вероятность отказа второго элемента
P2=F2(6)=1- 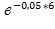 =
= 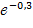 = 1- 0,741= 0, 259.
= 1- 0,741= 0, 259.
Искомая вероятность того, что оба элемента откажут, по теореме умножения вероятностей
P1= P2= 0,113*0,259 = 0,03.
б) Вероятность безотказной работы первого элемента
q1= R1(6)=  = 0,887.
= 0,887.
Вероятность безотказной работы второго элемента
q2= R2(6)= 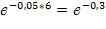 = 0,741.
= 0,741.
Искомая вероятность безотказной работы обоих элементов
q1*q2= 0,887*0,741=0,66.
в) Вероятность того, что откажет только один элемент
P1q2 +P2q1 = 0,113*0,741+0,259*0,887= 0,31.
г) Вероятность того, что хотя бы один элемент откажет
P=1- q1q2=1- 0,66 = 0,34
Ответ: а) 0,03; б) 0,887; в) 0,31; г) 0,34.
№ 370 Испытывают три элемента, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента F1(t) = 1- 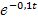 ; для второго F2(t) = 1-
; для второго F2(t) = 1- 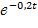 , для третьего элемента F3(t) = 1-
, для третьего элемента F3(t) = 1- 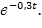 Найти вероятность того, что в интервале времени (0, 5)ч откажут: а) только один элемент; б) только два элемента; в) все три элемента.
Найти вероятность того, что в интервале времени (0, 5)ч откажут: а) только один элемент; б) только два элемента; в) все три элемента.
Решение.
а) Вероятность отказа первого элемента P1=F1(5)=1-  = 1- 0,607=0,393.
= 1- 0,607=0,393.
Вероятность безотказной работы первого элемента q1= R1(5)=  0,607.
0,607.
Вероятность отказа второго элемента P2=F2(5)=1-  = 1- 0,369=0,631.
= 1- 0,369=0,631.
Вероятность безотказной работы второго элемента q2= R2(5)= 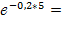 0,369.
0,369.
Вероятность отказа третьего элемента P3=F3(5)=1-  = 0,776.
= 0,776.
Вероятность безотказной работы третьего элемента q3= R3(5)= 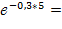 0,224.
0,224.
Искомая вероятность того, что только один элемент откажет: P1q2q3 + q1q3P2 + q1q2P3 =0.393∙0.369∙0.224 + 0.607∙0.631∙0.224 + 0.607∙0.369∙0.776= 0.292
б) Вероятность того, что откажут только 2 элемента P1P2q3 + P1q2P3 + q1P2P3 =0.393∙0.631∙0.224 + 0.393∙0.369∙0.776 + 0.607∙0.631∙0.776= 0.466
в) Вероятность того, что откажут все три элемента P1P2P3= 0.393∙0.631∙0.776= 0.19.
Ответ: а) 0,292; б) 0,466; в) 0,19.
№ 371 Производится испытание трех элементов, работающих независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону: для первого элемента f1(t) = 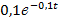 , для второго f2(t) =
, для второго f2(t) = 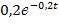 , для третьего элемента f3(t) =
, для третьего элемента f3(t) = 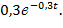 Найти вероятности того, что в интервале времени (0, 10) ч откажут: а) хотя бы один элемент; б) не менее двух элементов.
Найти вероятности того, что в интервале времени (0, 10) ч откажут: а) хотя бы один элемент; б) не менее двух элементов.
Решение.
б) Для того, чтобы узнать вероятность того, что в интервале времени (0, 10) ч откажут не менее двух элементов воспользуемся результатами задачи № 370 (как сказано в указании к задаче № 371)
P1q2q3 + q1q3P2 + q1q2P3 + P1P2q3 + P1q2P3 + q1P2P3= 0.466+ 0.19= 0.656.
Ответ: б) 0.656.
№ 372 Показательным законом надежности называют функцию надежности, определяемую равенством R(t)= 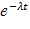 , где положительное число λ- интенсивность отказов. Доказать характеристическое свойство показательного закона надежности: вероятность безотказной работы элемента в интервале времени длительностью t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности интервала t (при заданной интенсивности отказов λ).
, где положительное число λ- интенсивность отказов. Доказать характеристическое свойство показательного закона надежности: вероятность безотказной работы элемента в интервале времени длительностью t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности интервала t (при заданной интенсивности отказов λ).
Решение.
Введем обозначений событий: А - безотказная работа элемента в интервале (0, t0) длительностью t0; В - безотказная работа элемента в интервале (t0, t0+ t) длительностью t.
Тогда АВ- безотказная работа в интервале (0, t0+ t) длительностью t0+ t.
По формуле R(t)= 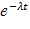 найдем вероятности этих событий:
найдем вероятности этих событий:
P(A)= 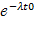 , P(B)=
, P(B)= 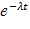 , P(AB)=
, P(AB)= 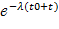 =
=  .
.
Найдем условную вероятность того, что элемент будет работать безотказно в интервале (t0, t0+ t) при условии, что он уже проработал безотказно в предшествующем интервале (0, t0):
PA(B)=  =
= 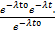 =
= 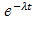 .
.
Так как в полученной формуле не содержится t0, а содержится только t, то это и означает, что время работы в предшествующем интервале не влияет на величину вероятности безотказной работы на последующем интервале, а зависит только от длины t последующего интервала (t0+ t), что и требовалось доказать.
Другими словами, условная вероятность PA(B) безотказной работы в интервале времени длительностью t, вычисленная в предположении, что элемент проработал безотказно на предшествующем интервале, равна безусловной вероятности P(B).
Кравченко Антонина
№373. Дискретная случайная величина X задана законом
распределения:
X 1 3 5
р 0,4 0,1 0,5
Найти закон распределения случайной величины Y = 3Х.
Решение.
Найдем возможные значения величины Y = 3Х.
Имеем:  . Видим, что различным
. Видим, что различным
возможным значениям X соответствуют различные значения Y. Это
объясняется тем, что функция  монотонная. Найдем
монотонная. Найдем
вероятности возможных значений Y. Для того чтобы Y = 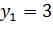 достаточно, чтобы величина X приняла значение
достаточно, чтобы величина X приняла значение 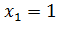 . Вероятность же события Х =1 по условию равна 0,4; следовательно, и вероятность события Y =
. Вероятность же события Х =1 по условию равна 0,4; следовательно, и вероятность события Y = 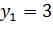 также равна 0,4.
также равна 0,4.
Аналогично получим вероятности остальных возможных значений Y:
P(Y=9)=P(X=3)=0,1
P(Y=15)=P(X=5)=0,5
Напишем искомый закон распределения Y:
Y 3 9 15
р 0,4 0,1 0,5
№374. Дискретная случайная величина X задана законом
распределения:
X 3 6 10
р 0,2 0,1 0,7
Найти закон распределения случайной величины Y = 2Х+1.
Решение.
Найдем возможные значения величины Y = 2Х+1.
Имеем: 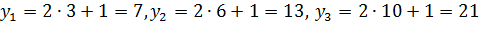 .Видим, что различным возможным значениям X соответствуют различные значения Y. Это объясняется тем, что функция
.Видим, что различным возможным значениям X соответствуют различные значения Y. Это объясняется тем, что функция 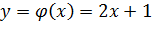 монотонная. Найдем
монотонная. Найдем
вероятности возможных значений Y. Для того чтобы Y =  достаточно, чтобы величина X приняла значение
достаточно, чтобы величина X приняла значение  . Вероятность же события Х =3 по условию равна 0,2; следовательно, и вероятность события Y =
. Вероятность же события Х =3 по условию равна 0,2; следовательно, и вероятность события Y =  также равна 0,2.
также равна 0,2.
Аналогично получим вероятности остальных возможных значений Y:
P(Y=13)=P(X=6)=0,1
P(Y=21)=P(X=10)=0,7
Напишем искомый закон распределения Y:
Y 7 13 21
р 0,2 0,1 0,7
№375. Дискретная случайная величина X задана законом
распределения:
X —1 —2 1 2
p 0,3 0,1 0,2 0,4
Найти закон распределения случайной величины 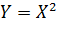
Решение.
Найдем возможные значения Y:


Итак, различным значениям X соответствуют одинаковые значения
Y. Это объясняется тем, что возможные значения X принадлежат
интервалу, на котором функция 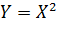 не монотонна.
не монотонна.
Найдем вероятности возможных значений Y. Для того чтобы






