Случайные величины и независимы. Найти дисперсию случайной величины , если из- известно, что , . 3 страница

Решение:

Так как события и противоположные, то сумма их вероятностей равна единице. Т.е.,

 

 

№238 Используя неравенство Чебышева в форме, приведенной в задаче 237, оценить вероятность того, что случайная величина X отклонится от своего математического ожидания не меньше чем на два средних квадратических отклонения.

Решение:

 

Ответ:

 

№239 Используя неравенство Чебышева, оценить вероятность того, что

Решение:

Ответ: P=0,9

 

№240 Дано: и

Используя неравенство Чебышева, оценить ε снизу.

Решение:

 

№241 Устройство состоит из 10 независимо-работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,05. С помощью неравенства Чебышева оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время Т окажется:

а) меньше двух;

б) не меньше двух.

 

Решение:

а) Обозначим через X дискретную случайную величину - число отказавших элементов за время Т. Тогда

M(X) =np=10*0.05=0.5

D(X) =npq=10*0.05*0.95=0.475

Воспользуемся неравенством Чебышева:

P (|X-M(X)|<e)>=1- (D(X)/e*e)

Подставив сюда М (Х)=0,5; D(X) =0,475, e = 2, получим

P (| X- 0.5 | <2)>=1-(0.475/4)=0.88

 

б) События |X-0.5|<2 и |X-0.5|>=2 противопоположны, поэтому сумма их вероятностей равна единице. Следовательно,

P (|X-0.5|>2)<=1-0.88=0.12

№243. Вероятность появления события А в каждом испытании равна 1/2. Используя неравенство Чебышева, оценить вероятность того, что число X появлений события А заключено в пределах от 40 до 60, если будет произведено 100 независимых испытаний.

Решение.

Найдем математическое ожидание и дисперсию дискретной

случайной величины X —числа появлений события А в 100

независимых испытаниях:

Найдем максимальную разность между заданным числом появле*

НИИ события и математическим ожиданием :

Воспользуемся неравенством Чебышева в форме

Подставляя M(X)=50, D(X)=25, = 10 получим

№244

Вероятность появления события А в каждом испытании равна ¼. Используя неравенство Чебышева, оценить вероятность того, что число Х появлений события А заключено в пределах от 150 до 250, если будет произведено 800 независимых испытаний.

Решение.

Найдем математическое ожидание и дисперсию дискретной случайной величины Х – числа появлений события А в 800 независимых испытаниях:

М(Х) = n*p = 800* ¼ = 200; D(X) = n*p*q= 800* ¼ * ¾ =150.

Найдем максимальную разность между заданным числом появлений события и математическим ожиданием М(Х) = 200:

ε = 250 – 200 = 10.

Воспользуемся неравенством Чебышева в форме

Р(|Х – М(Х)|< ε) ≥ 1 – D(X)/ε2.

Подставляя М(Х) = 200, D(X) = 150, ε=50, получим

Р(|Х – 200|< 50) ≥ 1 – 150/502 = 1 – 0,06 = 0,94.

№245 Дискретная случайная величина X задана законом распределения

X 0,3 0,6

р 0,2 0,8

Используя неравенство Чебышева, оценить вероятность

того, что |Х — М(Х)|<0,2.

Решение:

Найдем математическое ожидание и дисперсию величины X:

M(X)=0,3 0,2 + 0,6 0,8=0,54

D(X)=M(X2)-[M(X)]2= (0,32 0,2+0,62 0,8) – 0,542 =0,0144.

Воспользуемся неравенством Чебышева в форме

Р (| Х — М (X) | < ) ≥1-D (Х)/ 2

Подставляя М(Х)=0,54, D(X) =0,0144, =0,2, окончательно

получим

Р (| X- 0,54| < 0,2) ≥1 -0,0144/0,04 =0,64.

 

№246 Дискретная случайная величина X задана законом

распределения

X 0,1 0,4 0,6

р 0,2 0,3 0,5

Используя неравенство Чебышева, оценить вероятность

того, что |Х — М(Х)|<

Решение:

Найдем математическое ожидание и дисперсию величины X:

M(X)=0,1 0,2 + 0,4 0,3+0,6 0,5 = 0,44

D(X)=M(X2)-[M(X)]2= (0,12 0,2 + 0,42 0,3+0,62 0,5) – 0,442 =0,0364.

Воспользуемся неравенством Чебышева в форме

Р (| Х — М (X) | < ) ≥1-D (Х)/ 2

Подставляя М(Х)=0,44, D(X) =0,0364, = окончательно

получим

Р (| X- 0,44| < ) ≥1 -0,0364/0,4 =0,909.

 

№247 Последовательность независимых случайных величин задана законом распределения

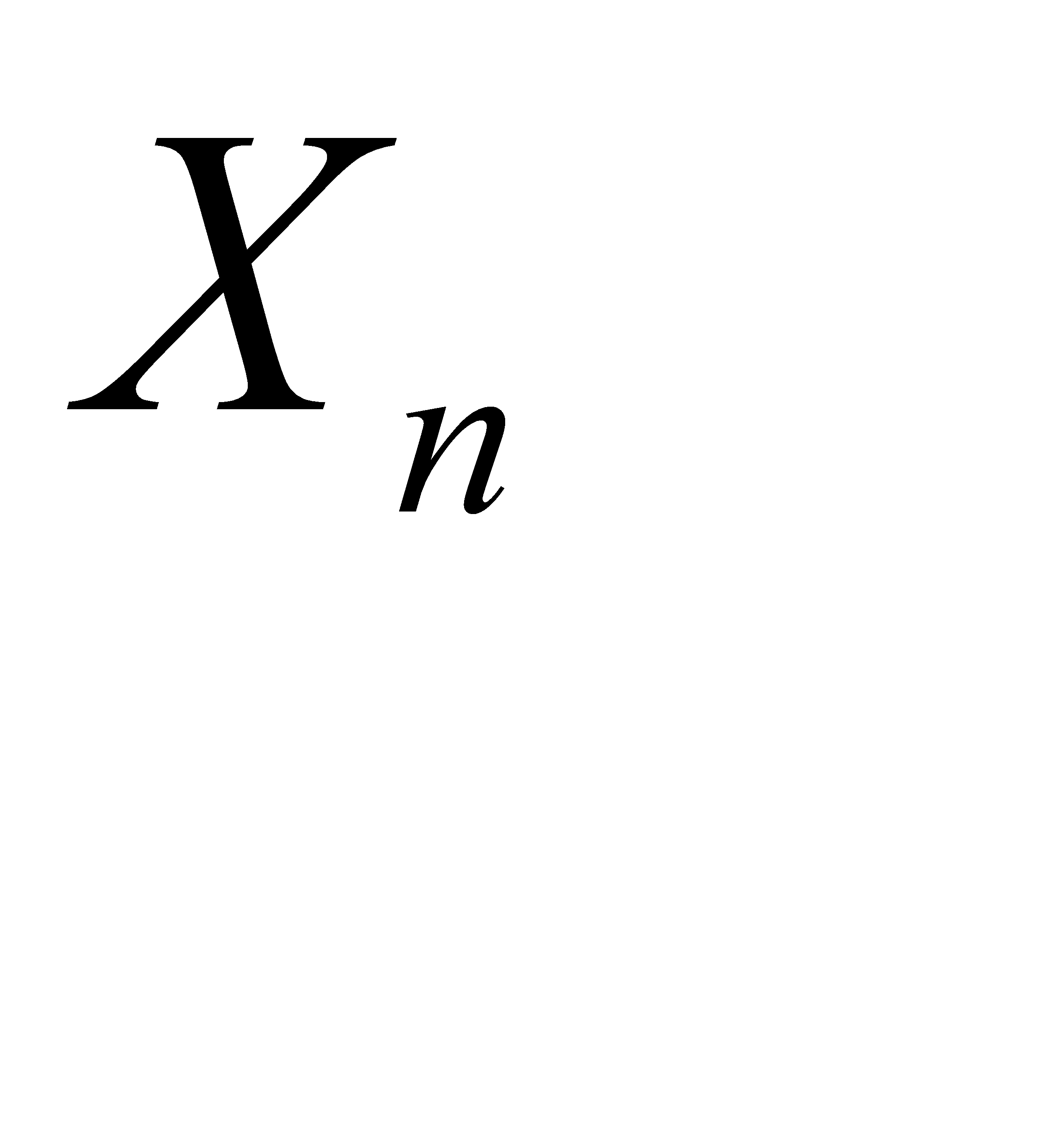
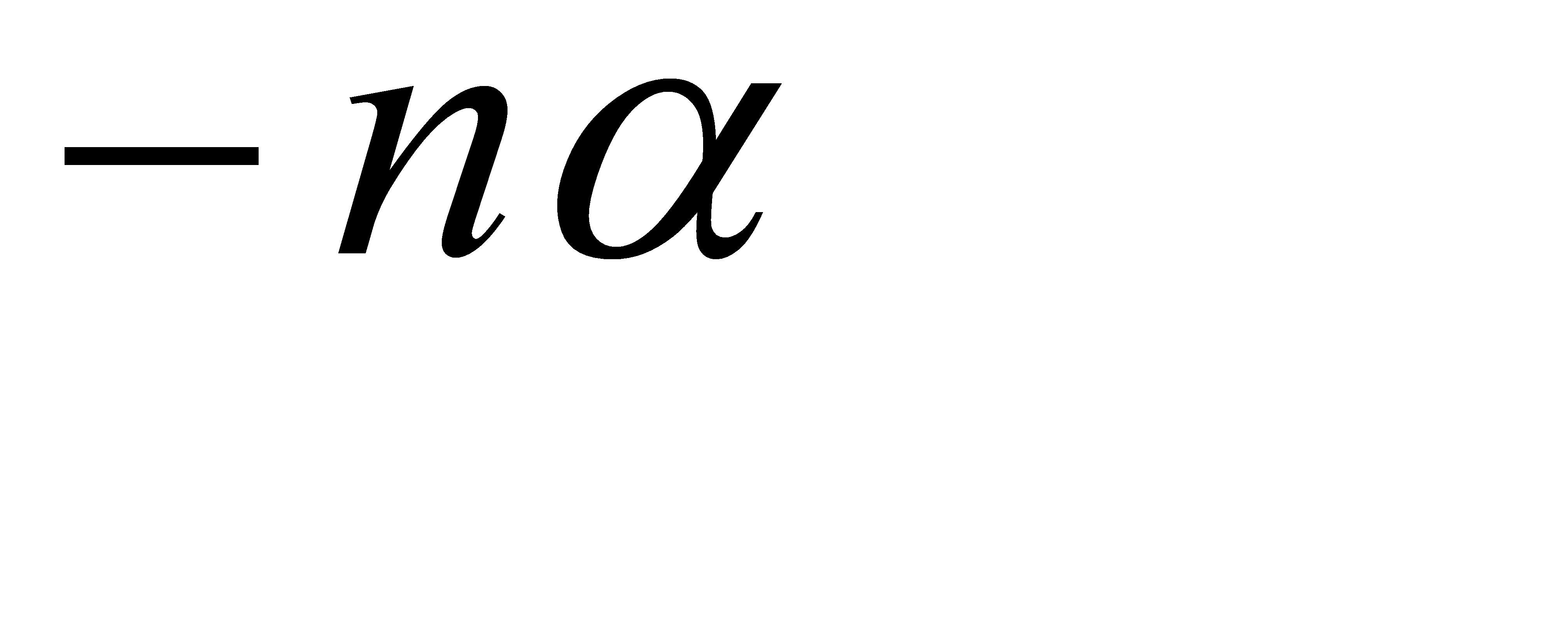
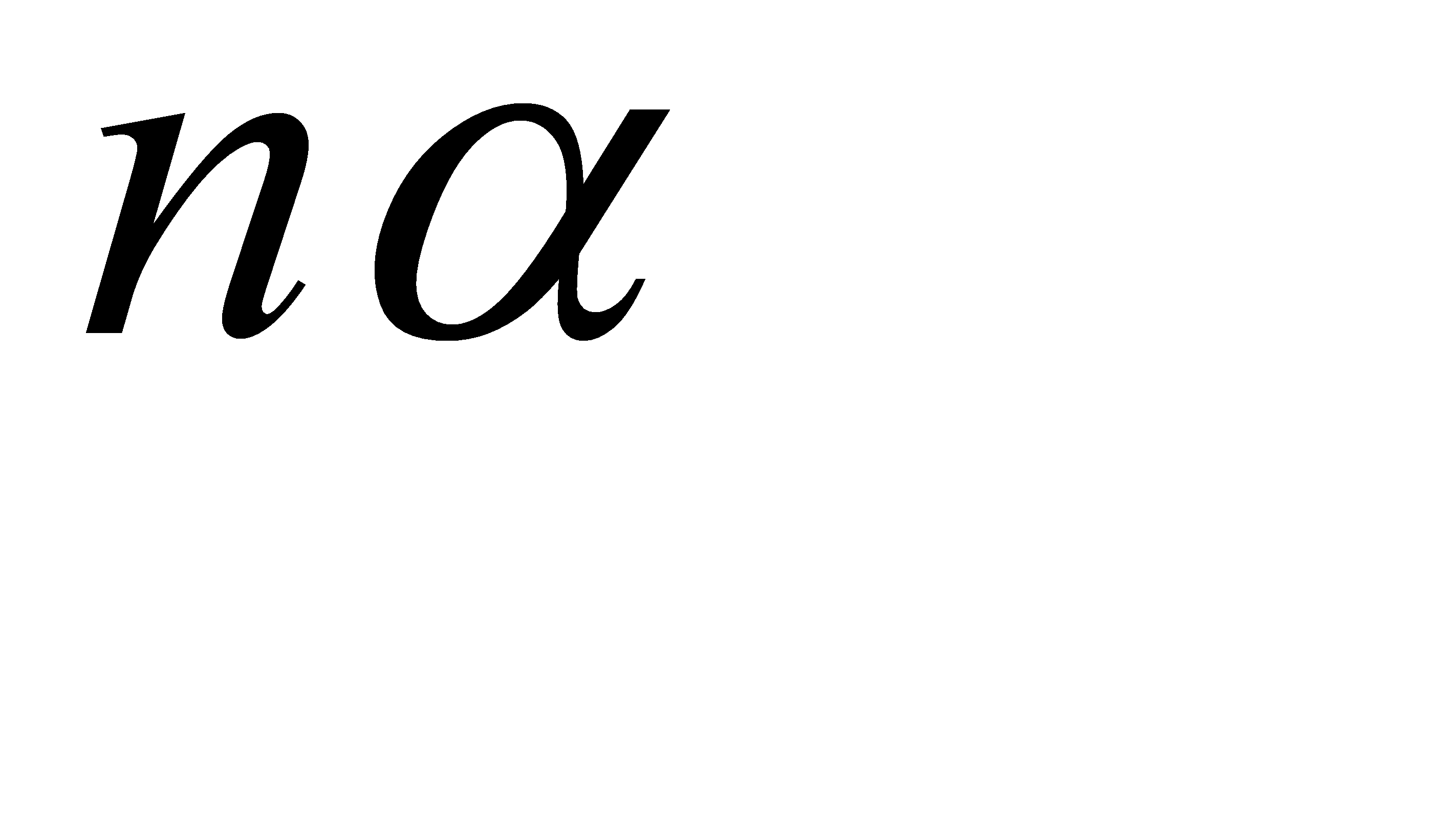
p

Применима ли к заданной последовательности теорема Чебышева?

Решение:

Для того, чтобы к последовательности случайных величин была применимы теорема Чебышева, достаточно, чтобы

1) эти величины были попарно независимы,

2) имели конечные математические ожидания,

3) имели равномерно ограниченные дисперсии.

Поскольку случайные величины независимы, то они подавно попарно независимы, т.е. первое требование теоремы Чебышева выполняется.

Проверим, выполняется ли требование конечности математических ожиданий:

 

 

Таким образом, каждая случайная величина имеет конечное (равное нулю) математическое ожидание, т.е. второе требование теоремы выполняется.

Проверим, выполняется ли требование равномерной ограниченности дисперсии. Напишем закон распределения :

p

или, сложив вероятности одинаковых возможных значений,

p

 

Найдём математическое ожидание :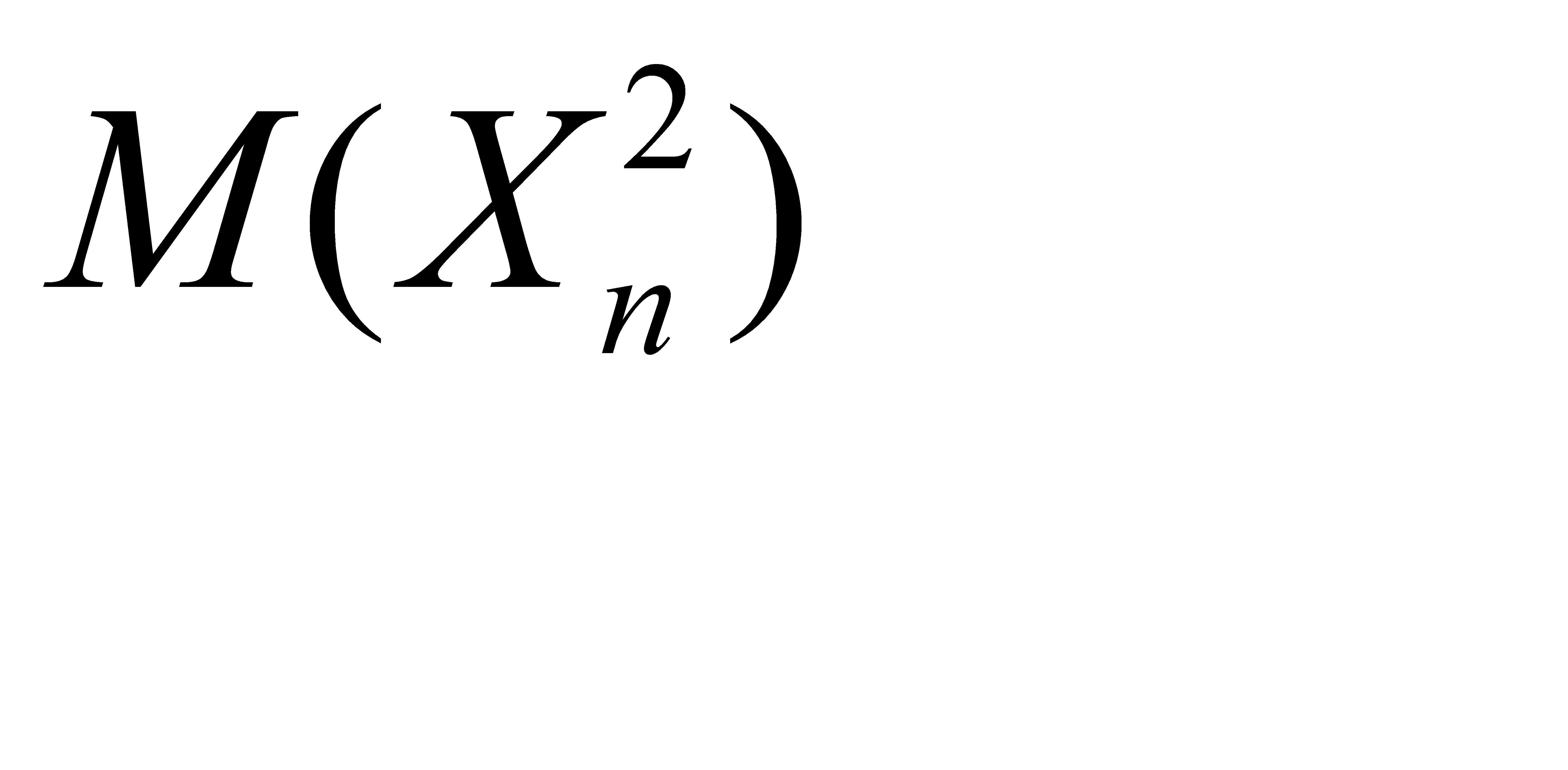

 

 

Найдём дисперсию :

 

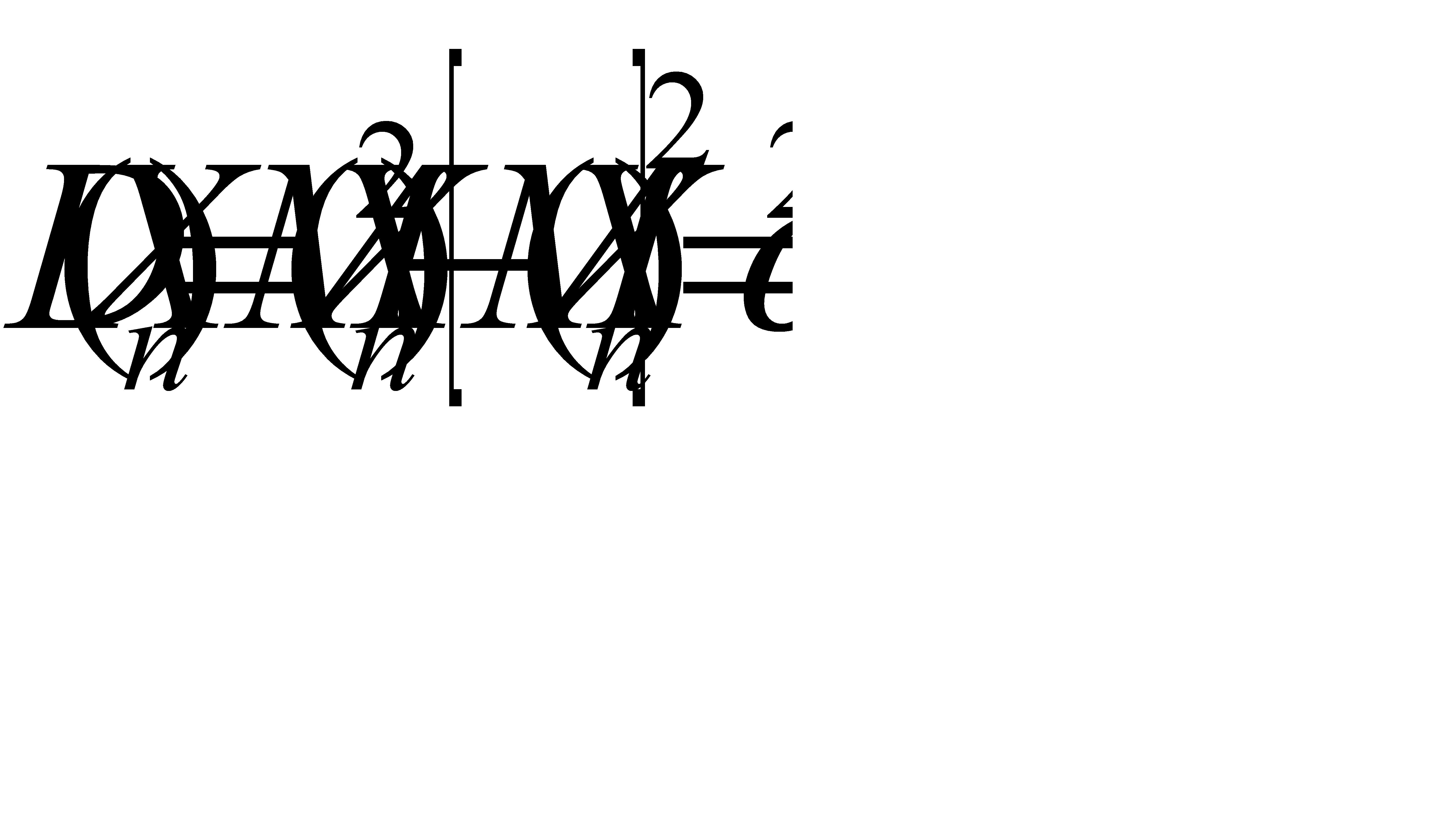
Таким образом, дисперсии заданных случайных величин равномерно ограничены

числом , т.е. третье требование выполняется.

Итак, поскольку все требования выполняются, к рассматриваемой последовательности случайных величин теорема Чебышева применима.

Ответ: применима.

 

№248 Последовательность независимых случайных величин задана законом распределения

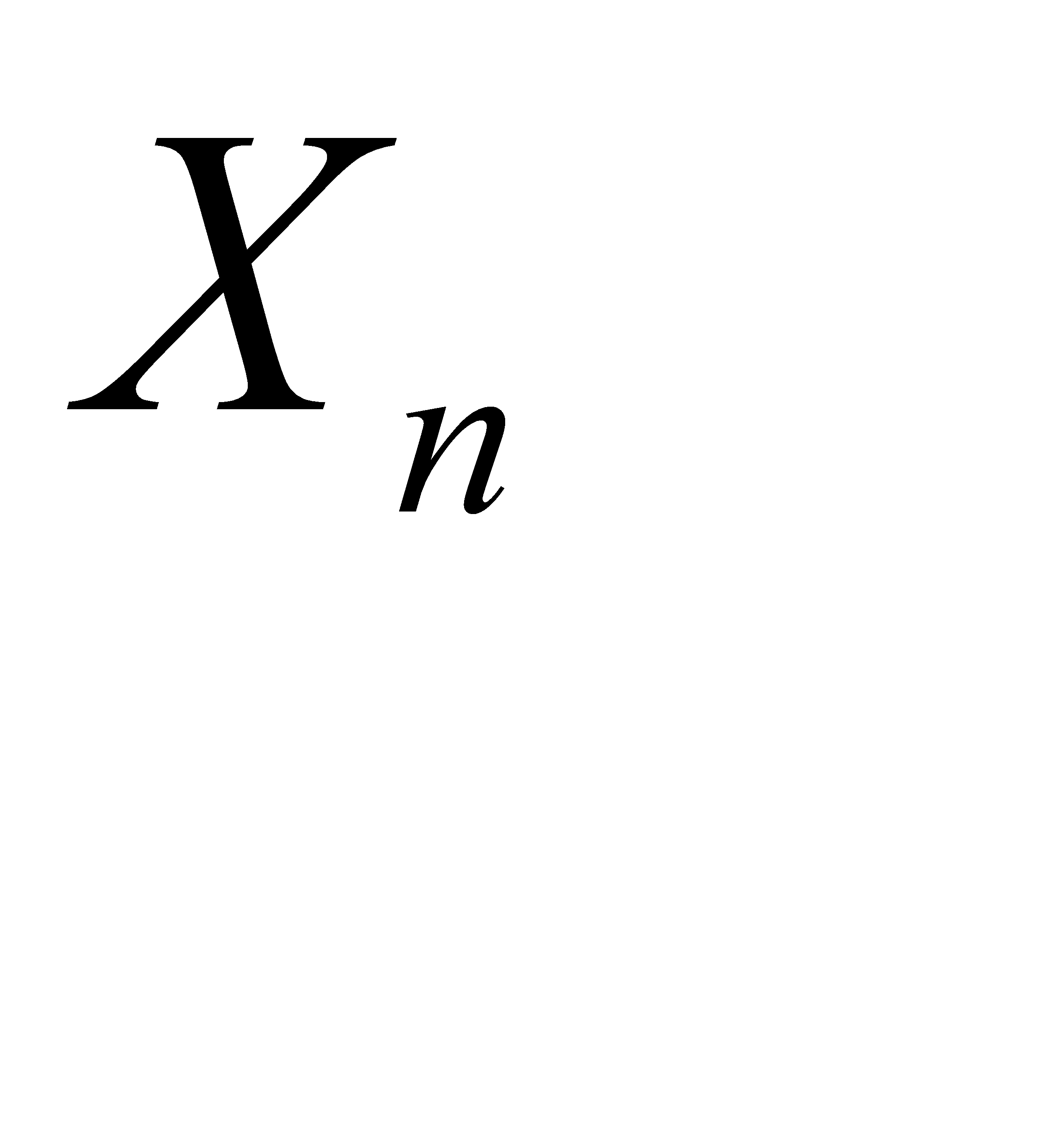
	a	-a
p

Применима ли к заданной последовательности теорема Чебышева?

Решение:

Для того, чтобы к последовательности случайных величин была применимы теорема Чебышева, достаточно, чтобы

1) эти величины были попарно независимы,

2) имели конечные математические ожидания,

3) имели равномерно ограниченные дисперсии.

Поскольку случайные величины независимы, то они подавно попарно независимы, т.е. первое требование теоремы Чебышева выполняется.

Проверим, выполняется ли требование конечности математических ожиданий:

 

 

Таким образом, каждая случайная величина имеет конечное (равное ) математическое ожидание, т.е. второе требование теоремы выполняется.

Проверим, выполняется ли требование равномерной ограниченности дисперсии. Напишем закон распределения :

	a 2	a 2
p

или, сложив вероятности одинаковых возможных значений,

	a 2
p

 

Найдём математическое ожидание :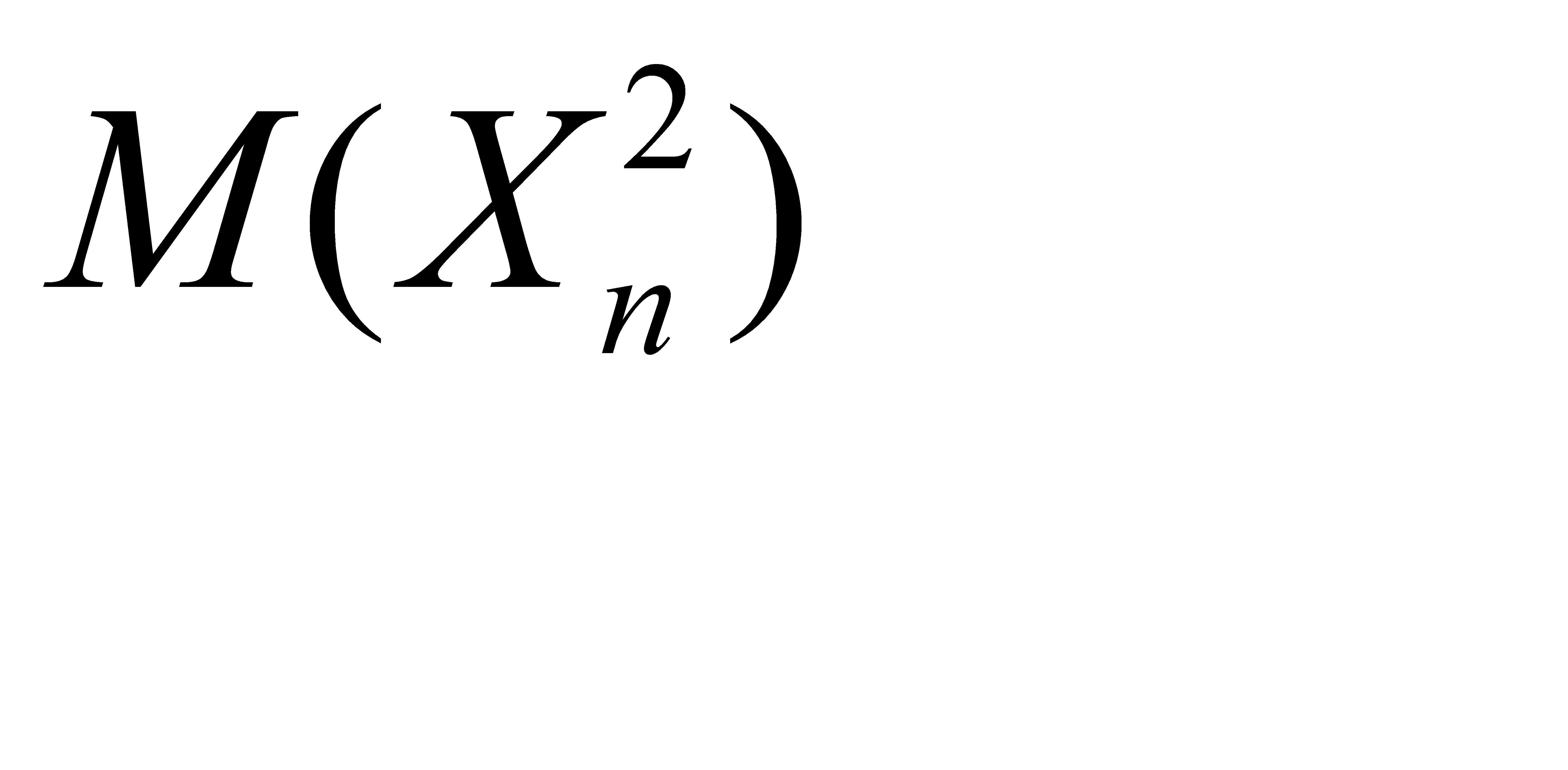

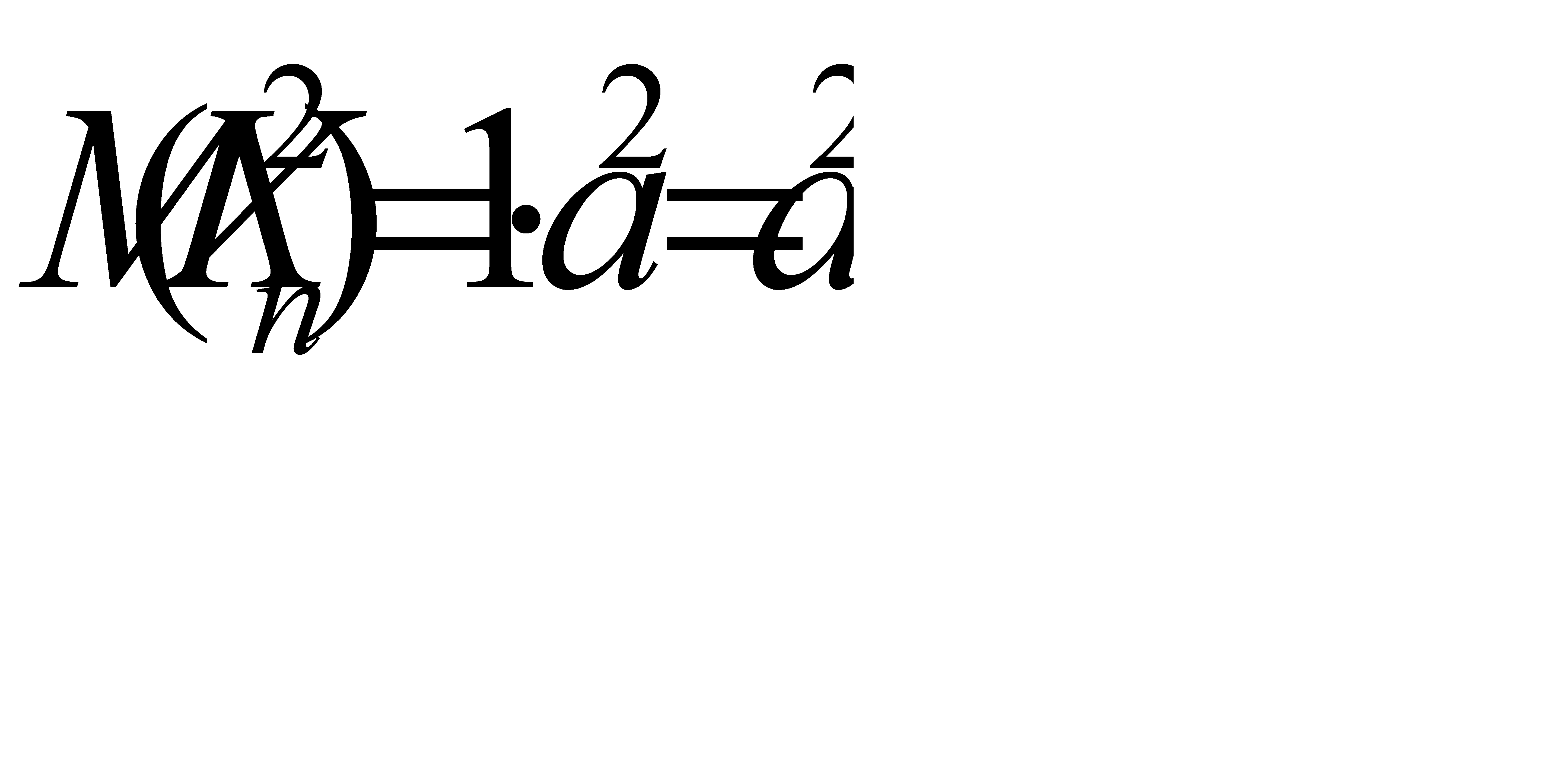
Найдём дисперсию :

Эта функция возрастает, следовательно, чтобы вычислить константу, ограничивающую дисперсию, можно вычислить предел:

 

Таким образом, дисперсии заданных случайных величин равномерно ограничены

числом , т.е. третье требование выполняется.

Итак, поскольку все требования выполняются, к рассматриваемой последовательности случайных величин теорема Чебышева применима.

 

Ответ: применима.

 

Спесивцева Наталья

№249 Последовательность независимых случайных величин задана законом распределения

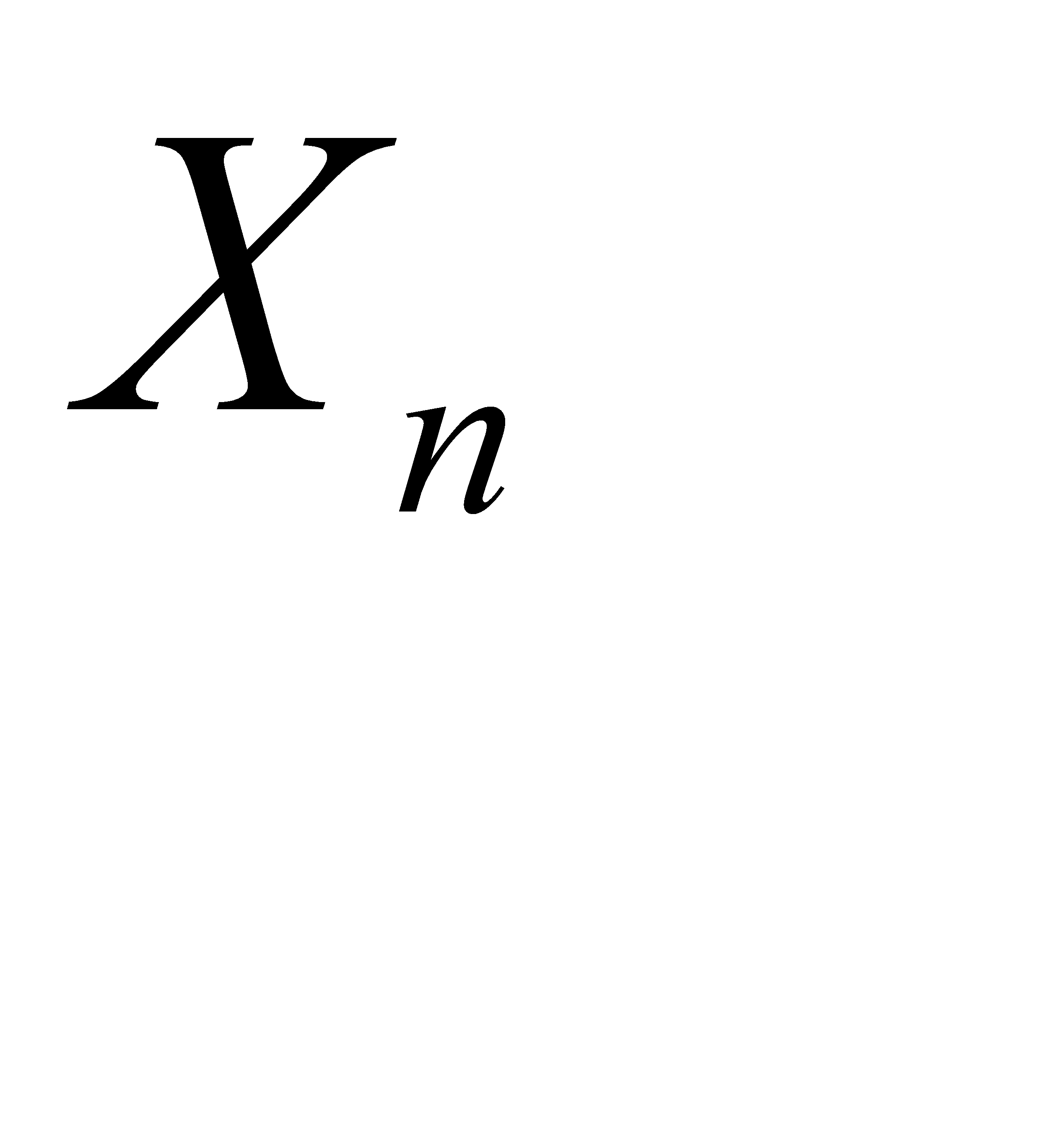
	n+1	-n
p

А) убедиться, что требование теоремы Чебышева о равномерной ограниченности дисперсии не выполняется

Б) можно ли отсюда заключить, что к рассматриваемой последовательности теорема Чебышева неприменима?

Решение:

А) Найдём математическое ожидание :

Проверим, выполняется ли требование равномерной ограниченности дисперсии. Напишем закон распределения :

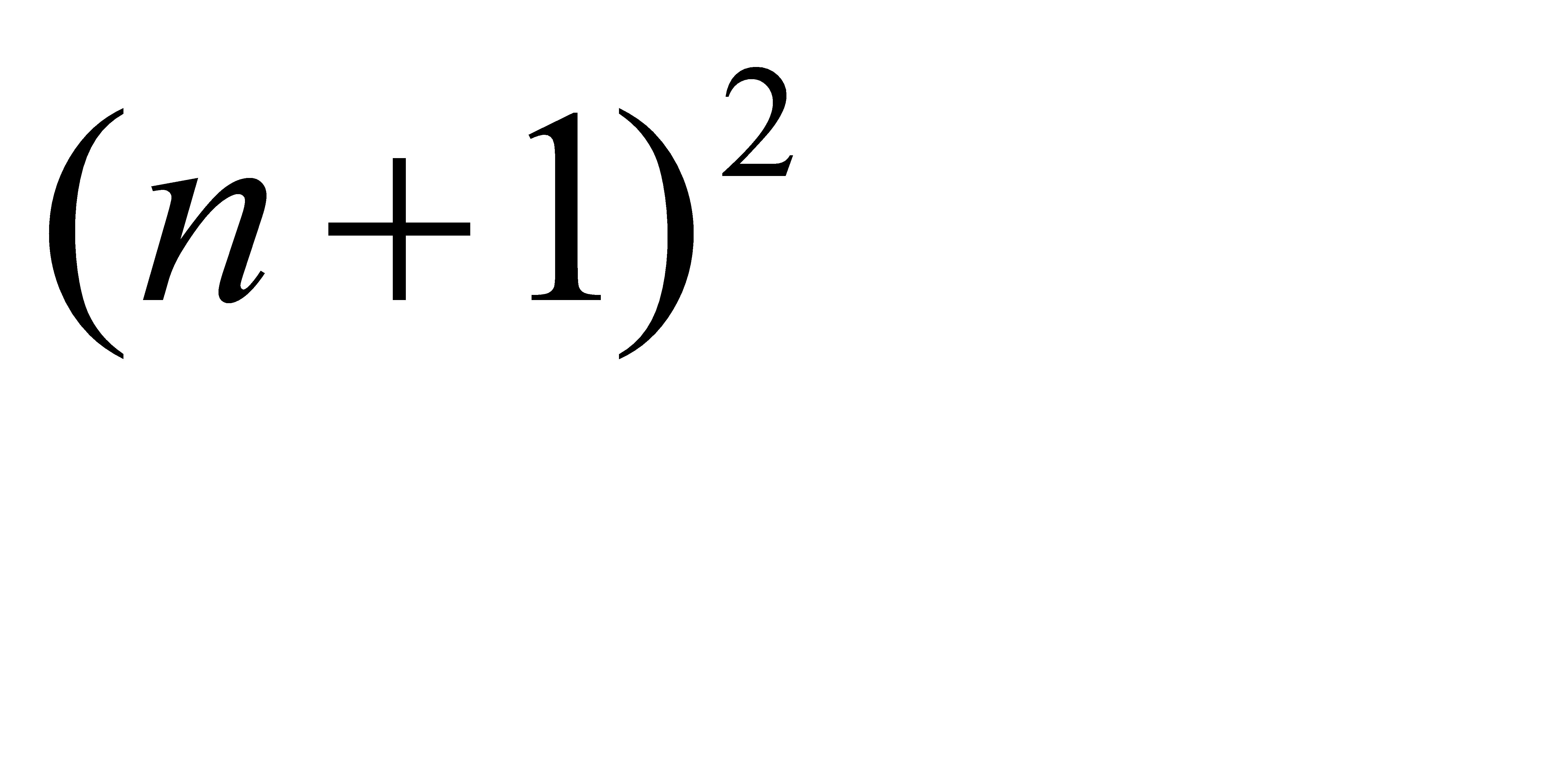
p

Найдём математическое ожидание :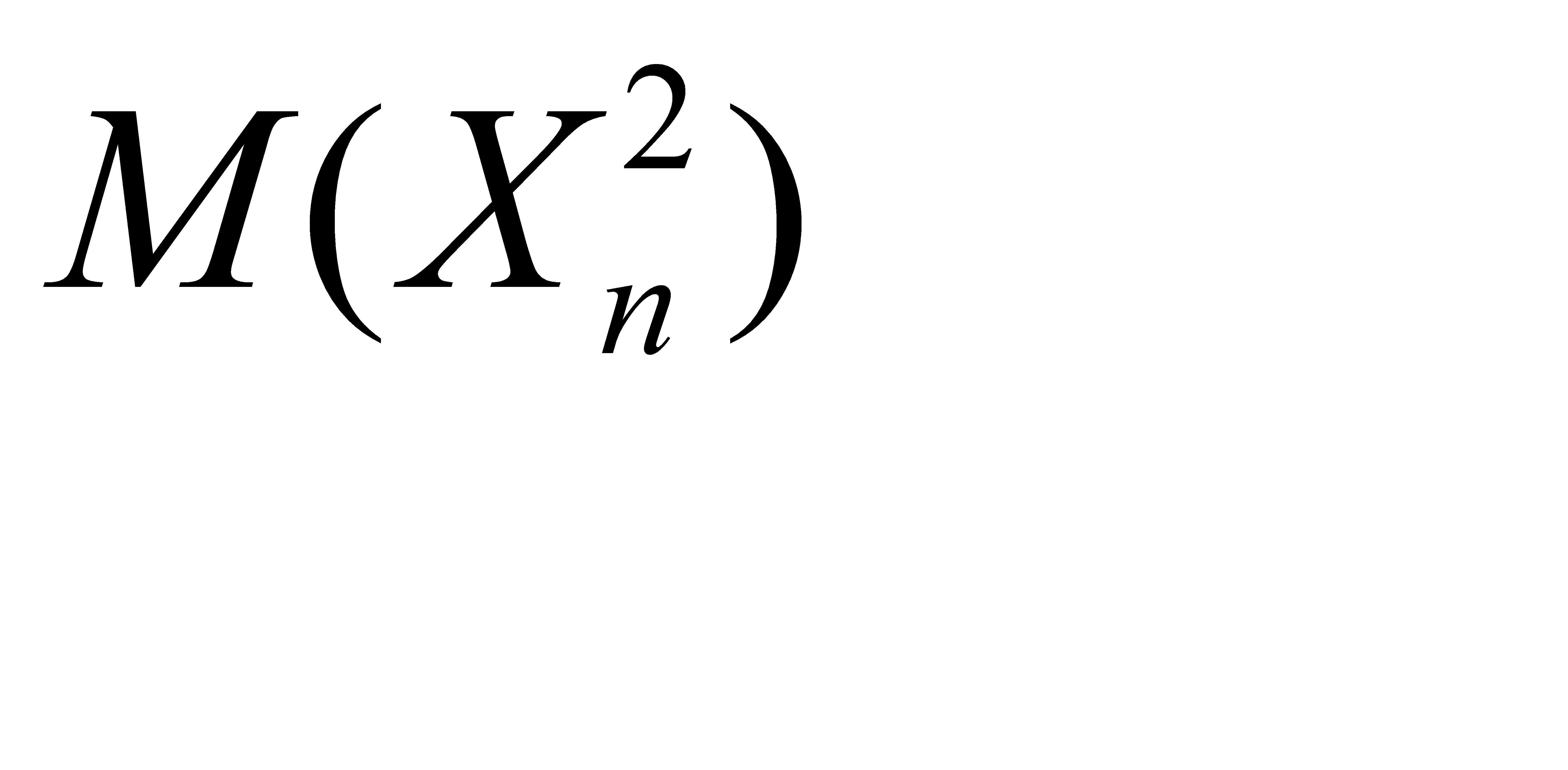

Найдём дисперсию :

Эта функция возрастает, следовательно, чтобы вычислить константу, ограничивающую дисперсию, можно вычислить предел:

Таким образом, дисперсии заданных случайных величин неограниченны, что и требовалось доказать.

Б) Из формулировки теоремы Чебышева следует, что требование равномерной ограниченности дисперсий является достаточным, но не необходимым условием, поэтому нельзя утверждать, что к данной последовательности эту теорему применить нельзя.

№250 Последовательность независимых случайных величин Х₁, Х₂, …, Х_n, … задана законом распределения

Применима ли к заданной последовательности теорема Чебышева?

Решение:

Поскольку случайные величины Х_n независимы, то они подавно и попарно независимы, т.е. первое требование теоремы Чебышева выполняется.

Легко найти, что M(X_n)=0, т.е.первое требование конечности математических ожиданий выполняется.

Остается проверить выполнимость требования равномерной ограниченности дисперсий. По формуле

D(X_n)=M(X_n²)-[M(X_n)]²,

учитывай, что M(X_n)=0, найдем (выкладки предоставляются выполнить читателю)

Временно предположим, что n изменяется непрерывно (чтобы подчеркнуть это допущение, обозначим n через х), и исследуем на экстремум функцию φ(х)=х²/2^х-1.

Приравняв первую производную этой функции к нулю, найдем критические точки х₁=0 и х₂=ln 2.

Отбросим первую точку как не представляющую интереса (n не принимает значения, равного нулю); легко видеть, что в точек х₂=2/ln 2 функция φ(х) имеет максимум. Учитывая, что 2/ln 2 ≈ 2.9 и что N – целое положительное число, вычислим дисперсию D(X_n)= (n²/2^n-1)α² для ближайших к числу 2.9 (слева и справа) целых чисел, т.е. для n=2 и n=3.

При n=2 дисперсия D(X₂)=2α², при n=3 дисперсия D(Х₃)=9/4α². Очевидно,

(9/4)α² > 2α².

Таким образом, наибольшая возможная дисперсия равна (9/4)α², т.е. дисперсии случайных величин Хn равномерно ограничены числом (9/4)α².

Итак, все требования теоремы Чебышева выполняются, следовательно, к рассматриваемой последовательности эта теорема применима.

 

№251 Последовательность независимых случайных величин X₁, X₂, …, X_n, … задана законом распределения

Применима ли к заданной последовательности теорема Чебышева?

Замечание. Поскольку случайные величины Х, одинаково распределены и независимы, то читатель, знакомый с теоремой Хинчина, может ограничиться вычислением лишь математического ожидания и убедиться, что оно кончено.

Решение:

Поскольку случайные величины Х_n независимы, то они подавно и попарно независимы, т.е. первое требование теоремы Чебышева выполняется.

Легко найти, что M(X_n)=0, т.е.первое требование конечности математических ожиданий выполняется.

Остается проверить выполнимость требования равномерной ограниченности дисперсий. По формуле

D(X_n)=M(X_n²)-[M(X_n)]²,

учитывай, что M(X_n)=0, найдем

D(X_n)=2

Таким образом, наибольшая возможная дисперсия равна 2, т.е. дисперсии случайных величин Х_n равномерно ограничены числом 2.

Итак, все требования теоремы Чебышева выполняются, следовательно, к рассматриваемой последовательности эта теорема применима.

№252 Случайная величина Х задана функцией распределения

Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (0, 1/3).

Решение:

Вероятность того, что Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: P(a<X<b)=F(b)-F(a). Положив а=0, b=1/3, получим

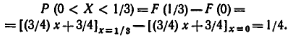
№253 Случайная величина Х задана на всей оси Ох функцией распределена F(x)=1/2+(arctg x)/π. Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (0, 1).

Решение:

Вероятность того, что Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: P(a<X<b)=F(b)-F(a). Положив а=0, b=1, получим

Р(0< Х <1) = F(1)-F(0) = [1/2+1/4]_x=1 - [1/2+0]_x=0 = 1/4

 

№254 Случайная величина Х функцией распределения

Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (-1, 1).

 

Решение:

Вероятность того, что Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: P(a<X<b)=F(b)-F(a). Положив а=-1, b=1, получим

Р(-1< Х <1) = F(1)-F(-1) = [1/2+5/6]_x=-1 – [1/2+1/6]_x=1 = 1/3.

 

 

№255 Функция распределения непрерывной случайной величины Х (времени безотказной работы некоторого устройства) равна F(х)=1-е-х/T(х≥0). Найти вероятность безотказной работы устройства за время х≥Т.

Решение:

Вероятность того, что Х примет значение, заключенное в интервале x≥T, равна приращению функции распределения на этом интервале: P(0<X<T)=F(T)-F(0). Положив это, получим

P(x≥T) = 1 - P(T<x) = 1 - P(0< X <T) = 1 – F(T)+F(0) = 1 - (1-1/e)+(1-1) = 1/e

 

№256 Случайная величина Х задана функцией распределения

Найти вероятность того, что в результате испытания Х примет значение: а) меньшее 0.2; б) меньшее трех; в) не меньшее трех; г) не меньшее пяти.

Решение:

а) Так как при х≤2 функция F(х)=0, то F(0, 2)=0, т.е. P(х < 0, 2)=0;

б) Р(Х < 3) = F(3) = [0.5x-1]_x=3 = 1.5-1 = 0.5;

в) события Х≥3 и Х<3 противоположны, поэтому Р(Х≥3)+Р(Х<3)=1. Отсюда, учитывая, что Р(Х<3)=0.5 [см. п. б.], получим Р(Х≥3) = 1-0.5 = 0.5;

г) сумма вероятностей противоположных событий равна единице, поэтому Р(Х≥5)+Р(Х<5)=1. Отсюда, используя условие, в силу которого при х>4 функция F(x)=1, получим Р(Х≥5) = 1-Р(Х<5) = 1-F(5) = 1-1 = 0.

 

№257 Случайная величина Х задана функцией распределения

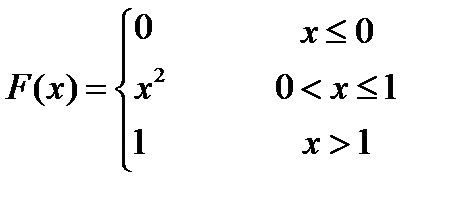
Найти вероятность того, что в результате четырех независимых испытаний величина Х ровно три раза примет значение, принадлежащее интервалу (0.25, 0.75).

Решение:

Вероятность того, что Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: P(a<X<b)=F(b)-F(a). Положив а=0.25, b=0.75, получим

P(0.25< X <0.75) = F(0.75)-F(0.25) = 0.5

Найдем вероятность того, что в результате четырех независимых испытаний величина Х ровно три раза примет значение, принадлежащее интервалу (0.25, 0.75). Для этого воспользуемся формулой Бернулли:

По условию n=4, k=3, p=0.5, q=1-0.5=0.5. Тогда

.

Ответ: 0,25.

 

№258 Случайная величина X задана на всей оси Ox функцией распределения . Найти возможное значения x₁, удовлетворяющее условию: с вероятностью ¼ случайная X в результате испытания примет значение большее x_{1 .}

Решение.

События X ≤ x₁ и X > x₁ - противоположные, поэтому . Следовательно, . Так как P(X=x₁) =0, то .

По определению функции распределения, .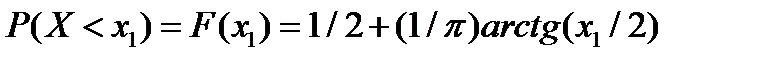

Следовательно, ½+(1/π)arctg(x₁/2)=(3/4), или . Отсюда x₁/2=1, или x₁=2.

Ответ: 2.

№259 Случайная величина X задана на всей оси Ox функцией распределения . Найти возможное значения x₁, удовлетворяющее условию: с вероятностью 1/6 случайная X в результате испытания примет значение большее x_{1 .}

Решение.

События X ≤ x₁ и X > x₁ - противоположные, поэтому . Следовательно, . Так как P(X=x₁) =0, то .

По определению функции распределения, .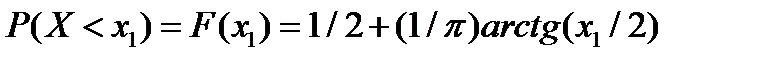

Следовательно, ½+(1/π)arctg(x₁/2)=(3/4), или . Отсюда, или .

 

№260 Дискретная случайная величина X задана законом распределения

X
p	0,5	0,2	0,3

 

Найти функцию распределения F(x) и начертить ее график.

Решение.

Если x ≤ 2, то F(x)=0. Действительно, значений меньших 2 величина X не принимает. Следовательно, при x ≤ 2 функция F(x)=P(X<x)=0.