Вывести полярное уравнение прямой, зная ее расстояние от полюса p и полярный угол нормали  .
Задача 0380
РЕШЕНИЕ. 1-Й СПОСОБ. На данной прямой s (рис.) возьмем произвольную точку М с полярными координатами .
Задача 0380
РЕШЕНИЕ. 1-Й СПОСОБ. На данной прямой s (рис.) возьмем произвольную точку М с полярными координатами  и и  . Точку пересечения прямой s с ее нормалью обозначим буквой Р. Из прямоугольного треугольника ОРМ находим: . Точку пересечения прямой s с ее нормалью обозначим буквой Р. Из прямоугольного треугольника ОРМ находим:
 (1)
Мы получили уравнение с двумя переменными (1)
Мы получили уравнение с двумя переменными  и и  , которму удовлетворяют координаты всякой точки М, лежащей на прямой s, и не удовлетворяют координаты никакой точки, не лежащей на этой прямой. Следовательно, уравнение (1) является уравнением прямой. Таким образом, задача решена. , которму удовлетворяют координаты всякой точки М, лежащей на прямой s, и не удовлетворяют координаты никакой точки, не лежащей на этой прямой. Следовательно, уравнение (1) является уравнением прямой. Таким образом, задача решена.
 2-Й СПОСОБ. Будем рассматривать декартову прямоугольную систему координат, положительная полуось абсцисс которой совпадает с полярной осью заданной полярной системы. В этой декартовой системе имеем нормальное уравнение прямой s:
2-Й СПОСОБ. Будем рассматривать декартову прямоугольную систему координат, положительная полуось абсцисс которой совпадает с полярной осью заданной полярной системы. В этой декартовой системе имеем нормальное уравнение прямой s:
 (2)
Воспользуемся формулами преобразования полярных координат в декартовы: (2)
Воспользуемся формулами преобразования полярных координат в декартовы:
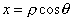 , ,  (3)
Подставив в уравнение (2) вместо х и у выражения (3), получим (3)
Подставив в уравнение (2) вместо х и у выражения (3), получим
 или
или
 . .
| ||
| Вывести полярное уравнение прямой, если даны: | ||
| 381.1 | Угол 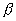 наклона прямой к полярной оси и длину перпендикуляра p,опущенного из полюса на эту пряму; написать уравнение этой прямой в случае наклона прямой к полярной оси и длину перпендикуляра p,опущенного из полюса на эту пряму; написать уравнение этой прямой в случае  , p=3; , p=3;

| |
| 381.2 | Отрезок а, который отсекает прямая на полярной оси, осчитая от полюса, и полярный угол  нормали этой прямой; написать уравнение этой прямой в случае а=2; нормали этой прямой; написать уравнение этой прямой в случае а=2;  ; ;

| |
| 381.3 | Угол 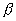 наклона прямой к полярной оси и отрезок а, который отекает прямая на полярной оси, считая от полюса; написать уравнение этой прямой в случае наклона прямой к полярной оси и отрезок а, который отекает прямая на полярной оси, считая от полюса; написать уравнение этой прямой в случае  , а=6. , а=6.
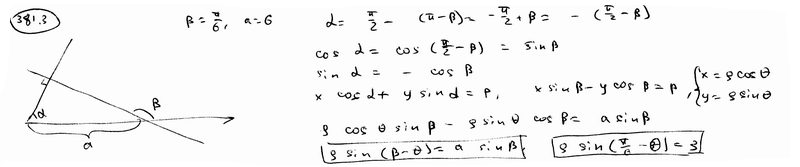
| |
Вывести полярное уравнение прямой, проходящей через точку M1( ; ;  ) и наклоненной к полярной оси под углом ) и наклоненной к полярной оси под углом 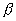 . .

| ||
Вывести полярное уравнение прямой, проходящей через точку M1( ; ;  ), полярный угол нормали которой равен ), полярный угол нормали которой равен  . .
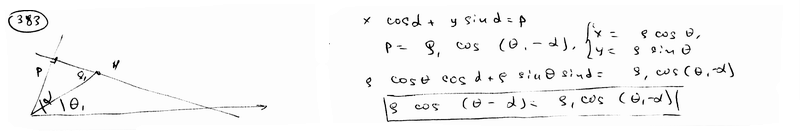
| ||
Составить уравнение прямой, проходящей через точки M1( ; ;  ) и M2( ) и M2( ; ;  ). ).

|
ЧАСТЬ 4. Геометрические свойства линий второго порядка
Глава 17. Окружность
| Составить уравнение окружности в каждом из следующих случаев: | ||
| 385.1 | центр окружности совпадает с началом координат и ее радиус R=3;

| |
| 385.2 | центр окружности совпадает с точкой С(2; -3) и ее радиус R=7;

| |
| 385.3 | окружность проходит через начало координат и ее центр совпадает с точкой С(6; -8);

| |
| 385.4 | окружность проходит через точку А(2; 6) и ее центр совпадает с точкой С(-1; 2);

| |
| 385.5 | точки А(3; 2) и В(-1; 6) являются концами одного из диаметров окружности;

| |
| 385.6 | центр окружности совпадает с началом координат и прямая  является касательной к окружности; является касательной к окружности;

| |
| 385.7 | центр окружности совпадает с точкой С(1; -1) и прямая  является касательной к окружности; является касательной к окружности;
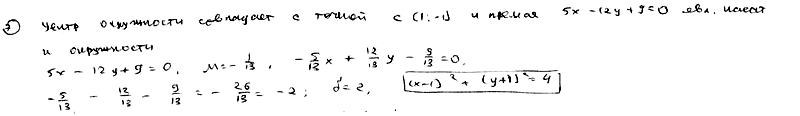
| |
| 385.8 | окружность проходит через точки А(3; 1) и В(-1; 3), а ее центр лежит на прямой 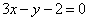 ; ;

| |
| 385.9 | окружность проходит через три точки А(1; 1), В(1; -1), С(2; 0);

| |
| 385.10 | окружность проходит через три точки: М1(-1; 5), М2(-2; -2). М3(5; 5).

| |
Точка С(3; -1) является центром окружности, отсекающей на прямой  хорду, длина которой равна 6. Составить уравнение этой окружности. хорду, длина которой равна 6. Составить уравнение этой окружности.

| ||
Написать уравнения окружностей радиуса  , касающихся прямой , касающихся прямой  в точке М1(3; 1). в точке М1(3; 1).

| ||
Составить уравнение окружности, касающейся прямых  , ,  , причем одна из них – в точке А(2; 1). , причем одна из них – в точке А(2; 1).

| ||
Составить уравнения окружностей, которые проходят через точку А(1; 0) и касаются прямых  , ,  . .

| ||
Составить уравнение окружности, которая, имея центр на прямой 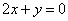 , касается прямых , касается прямых  , ,  . .

| ||
Составить уравнения окружностей, касающихся прямых  , ,  , причем одной из них – в точке М1(1; 2). , причем одной из них – в точке М1(1; 2).

| ||
Составить уравнения окружностей, проходящих через начало координат и касающихся прямых 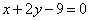 , ,  . .

| ||
Составить уравнение окружностей, которые, имея центры на прямой  , касаются прямых , касаются прямых  , ,  . .

| ||
Написать уравнения окружностей, проходящих через точку А(-1; 5) и касающихся прямых  , ,  . .

| ||
Написать уравнения окружностей, касающихся прямых  , ,  , ,  . .

| ||
Написать уравнения окружностей, касающихся прямых  , ,  , , 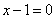 . .

| ||
| Какие из нижеприводимых уравнений определяют окружности? Найти центр С и радиус R каждой из них: | ||
| 397.1 |  ; ;
| |
| 397.2 | 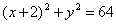 ; ;
| |
| 397.3 |  ; ;
| |
| 397.4 | 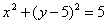 ; ;
| |
| 397.5 |  ; ;
| |
| 397.6 |  ; ;
| |
| 397.7 |  ; ;
| |
| 397.8 | 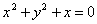 ; ;
| |
| 397.9 |  ; ;
| |
| 397.10 |  . .

| |
| Установить, какие линии определяются следующими уравнениями. Изобразить эти линии на чертеже. | ||
| 398.1 |  ; ;
| |
| 398.2 |  ; ;
| |
| 398.3 |  ; ;
| |
| 398.4 |  ; ;
| |
| 398.5 |  ; ;
| |
| 398.6 |  ; ;
| |
| 398.7 |  ; ;
| |
| 398.8 |  ; ;
| |
| 398.9 | 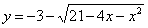 ; ;
| |
| 398.10 |  . .

| |
| Установить, как расположена точка А(1; -2) относительно каждой из следующих окружностей – внутри, вне или на контуре: | ||
| 399.1 |  ; ;
| |
| 399.2 |  ; ;
| |
| 399.3 |  ; ;
| |
| 399.4 |  ; ;
| |
| 399.5 |  . .

| |
| Определить уравнение линии центров двух окружностей, заданных уравнениями: | ||
| 400.1 |  и и 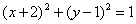 ; ;
| |
| 400.2 |  и и  ; ;
| |
| 400.3 |  и и  ; ;
| |
| 400.4 |  и и  . .

| |
Составить уравнение диаметра окружности  , перпендикулярного к прямой , перпендикулярного к прямой  . .

| ||
| Вычислить кратчайшее расстояние от точки до окружности в каждом из следующих случаев: | ||
| 402.1 | А(6; -8),  ; ;
| |
| 402.2 | В(3; 9),  ; ;
| |
| 402.3 | С(-7; 2),  . .

| |
Определить координаты точек пересечения прямой  и окружности и окружности  . .

| ||
| Определить, как расположена прямая относительно окружности (пересекает ли, касаетлся или проходит вне ее), если прямая и окружность заданы следующими уравнениями: | ||
| 404.1 |  , ,  ; ;
| |
| 404.2 | 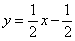 , ,  ; ;
| |
| 404.3 |  , ,  . .

| |
Определить, при каких значениях углового коэффициента k прямая  : :
| ||
| 405.1 | пересекает окружность  ; ;
| |
| 405.2 | касается этой окружности; | |
| 405.3 | проходит вне этой окружности.

| |
Вывести условие, при котором прямая  касается окружности касается окружности  . .

| ||
Составить уравнние диаметра окружности 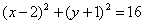 , проходящего через середину хорды, отсекаемой на прямой , проходящего через середину хорды, отсекаемой на прямой  . .

| ||
Составить уравнение хорды окружности  , делящейся в точке М(8,5; 3,5) пополам. , делящейся в точке М(8,5; 3,5) пополам.

| ||
Определить длину хорды окружности  , делящейся в точке А(1; 2) пополам. , делящейся в точке А(1; 2) пополам.

| ||
Дано уравнение пучка прямых 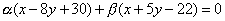 . Найти прямые этого пучка, на которых окружность . Найти прямые этого пучка, на которых окружность  отсекает хорды длиною отсекает хорды длиною 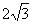 . .

| ||
Даны окружности  , ,  , пересекающиеся в точках М1(x1, y1), М2(x2, y2). Доказать, что любая окружность, проходящая через точки М1, М2, а также прямая М1М2 могут быть определены уравнением вида , пересекающиеся в точках М1(x1, y1), М2(x2, y2). Доказать, что любая окружность, проходящая через точки М1, М2, а также прямая М1М2 могут быть определены уравнением вида  при надлежащем выборе числе при надлежащем выборе числе  и и 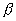 . .

| ||
Составить уравнение окружности, проходящей через точку А(1; -1) и точки пересечения окружностей  , , 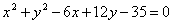 . .

| ||
Составить уравнение окружности, проходящей через начало координат и точки пересечения окружностей  , ,  . .

| ||
Составить уравнение прямой, проходящей через точки пересечения окружностей  , ,  . .

| ||
Вычислить расстояние от центра окружности 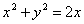 до прямой, проходящей через точки пересечения окружностей до прямой, проходящей через точки пересечения окружностей  , ,  . .

| ||
Определить длину общей хорды окружностей  , ,  . .

| ||
Центр окружности лежит на прямой  . Составить уравнение этой окружности, если известно, что она проходит через точки пересечения окружностей . Составить уравнение этой окружности, если известно, что она проходит через точки пересечения окружностей  , ,  . .

| ||
Составить уравнение касательной к окружности  в точке А(-1; 2). в точке А(-1; 2).

| ||
Составить уравнение касательной к окружности  в точке А(-5; 7). в точке А(-5; 7).

| ||
На окружности  найти точку М1, ближайшую к прямой найти точку М1, ближайшую к прямой  , и вычислить расстояние d от точки М1 до этой прямой. , и вычислить расстояние d от точки М1 до этой прямой.

| ||
Точка М1(x1, y1) лежит на окружности  . Составить уравнение касательной к этой окружности в точке М1. . Составить уравнение касательной к этой окружности в точке М1.
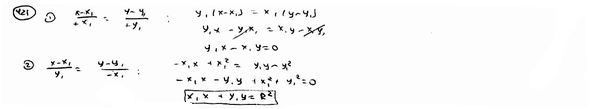
| ||
Точка М1(x1, y1) лежит на окружности  . Составить уравнение касательной к этой окружности в точке М1. . Составить уравнение касательной к этой окружности в точке М1.
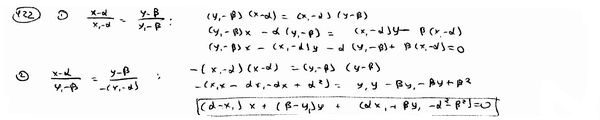
| ||
Определить острый угол, образованный при пересечении прямой 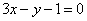 и окружности и окружности  (углом между прямой и окружности называется угол между прямой и касательной к окружности, проведенной к точке их пересечения). (углом между прямой и окружности называется угол между прямой и касательной к окружности, проведенной к точке их пересечения).

| ||
Определить, при каким углом пересекаются окружности  , , 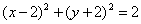 (углом между окружностями называется угол между их касательными в точке пересечения). (углом между окружностями называется угол между их касательными в точке пересечения).

| ||
Вывести условие, при котором окружности  , ,  пересекаются под прямым углом. пересекаются под прямым углом.

| ||
Доказать, что окружности  , ,  пересекаются под прямым углом. пересекаются под прямым углом.
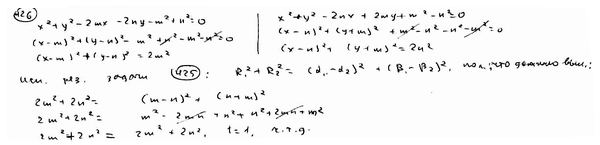
| ||
Из точки А(5/3; -5/3) проведены касательной к окружности  . Составить их уравнения. . Составить их уравнения.

| ||
Из точки А(1; 6) проведены касательные к окружности 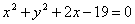 . Составить их уравнения. . Составить их уравнения.

| ||
Дано уравнение пучка прямых  . Найти прямые этого пучка, которые касаются окружности . Найти прямые этого пучка, которые касаются окружности  . .

| ||
Из точки А(4; 2) проведены касательные к окружности  . Определить угол, образованный этими касательными. . Определить угол, образованный этими касательными.

| ||
Из точки Р(2; -3) проведены касательные к окружности  . Составить уравнение хорды, соединяющий точки касания. . Составить уравнение хорды, соединяющий точки касания.

| ||
Из точки С(6; -8) проведены касательные к окружности  . Вычислить расстояние d от точки С до хорды, соединяющей точки касания. . Вычислить расстояние d от точки С до хорды, соединяющей точки касания.

| ||
Из точки Р(-9; 3) проведены касательные к окружности 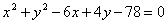 . Вычислить расстояние d от центра окружности до хорды, соединяющей точки касания. . Вычислить расстояние d от центра окружности до хорды, соединяющей точки касания.

| ||
Из точки Р(4; -4) проведены касательные к окружности  . Вычислить длину d хорды, соединяющей точки касания. . Вычислить длину d хорды, соединяющей точки касания.

| ||
Вычислить длину касательной, проведенной из точки А(1; -2) к окружности 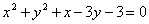 . .

| ||
Составить уравнение касательных к окружности 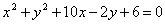 , параллельных прямой , параллельных прямой  . .

| ||
Составить уравнения касательных к окружности  , перпендикулярных к прямой , перпендикулярных к прямой  . .

| ||
Составить уравнение окружности в полярных координатах в полярных координатах по данному радиусу R и полярным координатам центра C(R,  ). ).

| ||
| Составить уравнение окружности в полярных координатах по данному радиусу R и полярным координатам центра окружности: | ||
| 439.1 | C(R, 0); | |
| 439.2 | C(R,  ); );
| |
| 439.3 | C(R,  ); );
| |
| 439.4 | C(R,  ). ).

| |
| Определить полярные координаты центра и радиус каждой из следующих окружностей: | ||
| 440.1 |  ; ;
| |
| 440.2 |  ; ;
| |
| 440.3 |  ; ;
| |
| 440.4 |  ; ;
| |
| 440.5 |  ; ;
| |
| 440.6 |  ; ;
| |
| 440.7 |  ). ).
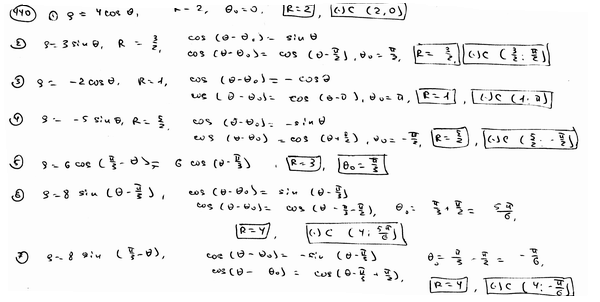
| |
| Окружности заданы уравнениями в полярных координатах. Составить их уравнения в декартовых прямоугольных координатах при условии, что полярная ось совпадает с положительной полуосью Ох, а полюс – с началом координат. | ||
| 441.1 |  ; ;
| |
| 441.2 |  ; ;
| |
| 441.3 |  . .

| |
| Окружности заданы уравнениями в декартовых прямоугольных координатах. Составить уравнения этих окружностей в полярных координатах при условии, что полярная ось совпадает с положительной полуосью Ох, а полюс – с началом координат. | ||
| 442.1 |  ; ;
| |
| 442.2 |  ; ;
| |
| 442.3 |  ; ;
| |
| 442.4 |  ; ;
| |
| 442.5 |  . .

| |
Составить полярное уравнение касательной к окружности  в точке М1(R, в точке М1(R,  ). ).

|






