Глава 20. Парабола
| Составить уравнение параболы, вершина которой находится в начале координат, зная, что: | ||
| 583.1 | парабола расположена в правой полуплоскости, симметрично относительно оси Ох и ее параметр р=3; | |
| 583.2 | парабола расположена в левой полуплоскости симетрично относительно оси Ох и ее параметр р=0,5. | |
| 583.3 | парабола расположена в верхней полуплоскости симметрично относительно оси Оу и ее параметр р=1/4. | |
| 583.4 | парабола расположена в нижней полуплоскости симметрично оси Оу и ее параметр р=3.
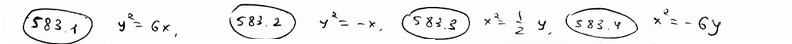
| |
| Определить величину параметра и расположение относительно координатных осей следующих парабол: | ||
| 584.1 | 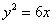 ; ;
| |
| 584.2 | 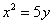 ; ;
| |
| 584.3 | 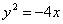 ; ;
| |
| 584.4 | 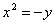 . .

| |
| Составить уравнение параболы, вершина которой находится в начале координат, зная, что: | ||
| 585.1 | парабола расположена симметрично относительно оси Ох и проходит через точку А(9; 6); | |
| 585.2 | парабола расположена симметрично относительно оси Ох и проходит через точку В(-1; 3); | |
| 585.3 | парабола расположена симметрично относительно оси Оу и проходит через точку С(1; 1); | |
| 585.4 | парабола расположена симметрично относительно оси Оу и проходит через точку D(4; -8).

| |
Стальной трос подвешен за два конца; точки крепления расположены на одинаковой высоте; расстояние между ними равно 20 см. Величина его прогиба на расстоянии 2 м от точки крепления, считая по горизонтали, равна 14,4 см. Определить величину прогиба этого троса в середине между точками крепления, приближенно считая, что трос имеет форму дуги параболы.
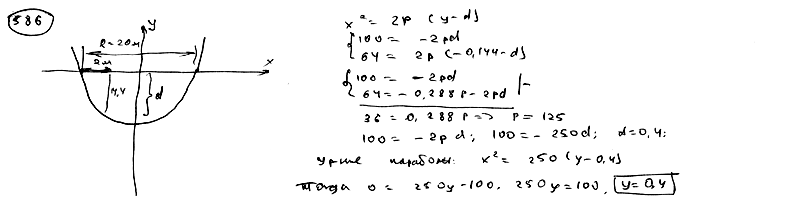
| ||
Составить уравнение параболы, которая имеет фокус Е(0; -3) и проходит через начало координат, зная, что ее осью служит ось Оу.
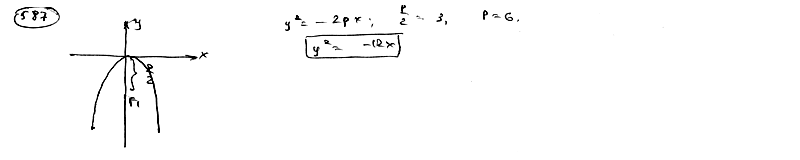
| ||
| Установить, какие линии определяются следующими уравнениями. Изобразить эти линии на чертеже. | ||
| 588.1 | 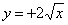 ; ;
| |
| 588.2 | 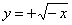 ; ;
| |
| 588.3 | 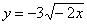 ; ;
| |
| 588.4 | 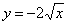 ; ;
| |
| 588.5 | 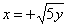 ; ;
| |
| 588.6 | 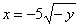 ; ;
| |
| 588.7 | 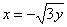 ; ;
| |
| 588.8 | 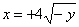 . .
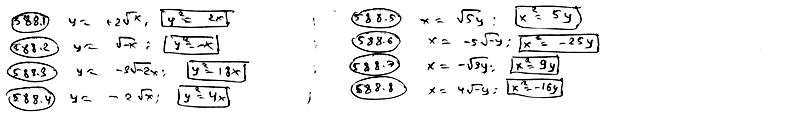
| |
Найти фокус F и уравнение директрисы параболы 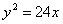 . .

| ||
Вычислить фокальный радиус точки М параболы 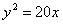 , если абсцисса точки М равна 7. , если абсцисса точки М равна 7.
| ||
Вычислить фокальный радиус точки М параболы 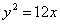 , если ордината точки М равна 6. , если ордината точки М равна 6.

| ||
На параболе 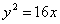 найти точки, фокальный радиус которых равен 13. найти точки, фокальный радиус которых равен 13.
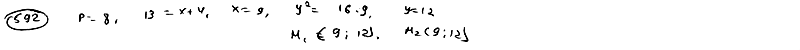
| ||
Составить уравнение параболы, если дан фокус F(-7; 0) и уравнение директрисы 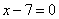 . .
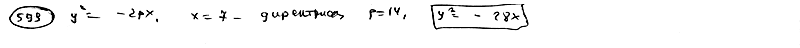
| ||
Составить уравнение параболы, зная, что ее вершина совпадает с точкой ( ; ; 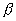 ), параметр равен p, ось параллельна оси Ох и парабола простирается в бесконечность: ), параметр равен p, ось параллельна оси Ох и парабола простирается в бесконечность:
| ||
| 594.1 | в положительном направлении оси Ох; | |
| 594.2 | в отрицательном направлении оси Ох.

| |
Составить уравнение параболы, зная, что ее вершина совпадает с точкой ( ; ; 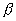 ), параметр равен p, ось параллельна оси Оу и парабола простирается в бесконечность: ), параметр равен p, ось параллельна оси Оу и парабола простирается в бесконечность:
| ||
| 595.1 | в положительном направлении оси Оу (т.е. парабола является восходящей); | |
| 595.2 | в отрицательном направлении оси Оу (т.е. парабола являетя нисходящей).

| |
| Установить, что каждое из следующих уравнений определяет параболу, и найти ее вершины А, величину параметра р и уравнение директрисы: | ||
| 596.1 | 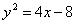 ; ;
| |
| 596.2 | 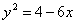 ; ;
| |
| 596.3 | 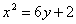 ; ;
| |
| 596.4 | 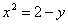 . .
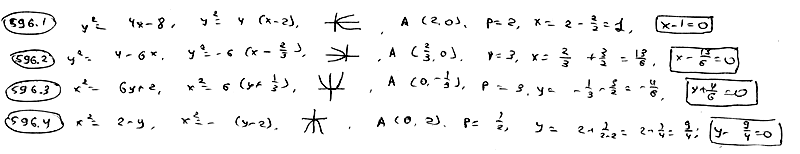
| |
| Установить, что каждое из следующих уравнений определяет параболу, и найти координаты ее вершины А и величину параметра р: | ||
| 597.1 | 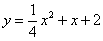 ; ;
| |
| 597.2 | 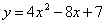 ; ;
| |
| 597.3 | 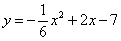 . .
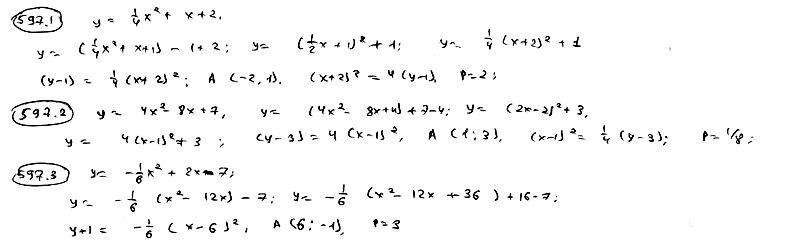
| |
| Установить, что каждое из следующих уравнений определяет параболу, и найти ее вершины А и величину параметра р: | ||
| 598.1 | 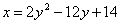 ; ;
| |
| 598.2 | 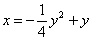 ; ;
| |
| 598.3 | 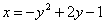 . .
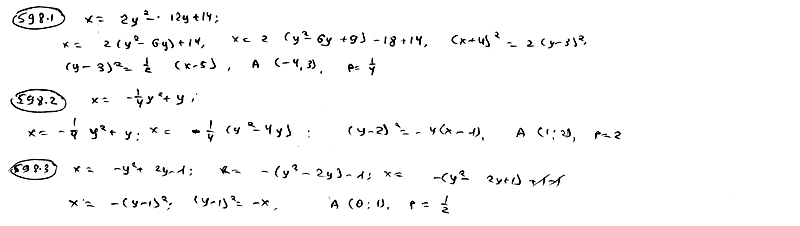
| |
| Установить, какие линии определяются следующими уравнениями: | ||
| 599.1 | 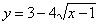 ; ;
| |
| 599.2 | 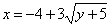 ; ;
| |
| 599.3 | 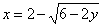 ; ;
| |
| 599.4 | 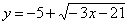 . .
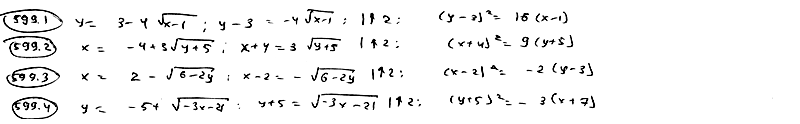
| |
Составить уравнение параболы, если даны ее фокус F(4; 3) и директриса 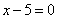 . .
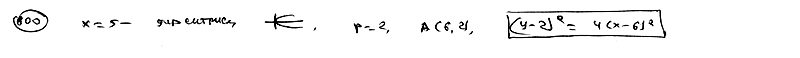
| ||
Составить уравнение параболы, если даны ее фокус F(4; 3) и директриса 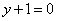 . .
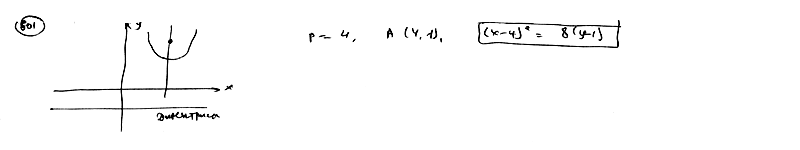
| ||
Составить уравнение параболы, если даны ее фокус F(2; -1) и директриса  . .

| ||
Даны вершина параболы А(6; -3) и уравнение ее директрисы 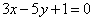 . Найти фокус F этой параболы. . Найти фокус F этой параболы.

| ||
Даны вершина параболы А(-2; -1) и уравнение е директрисы  . Составить уравнение этой параболы. . Составить уравнение этой параболы.

| ||
Определить точки пересечения прямой 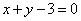 и параболы и параболы 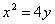 . .
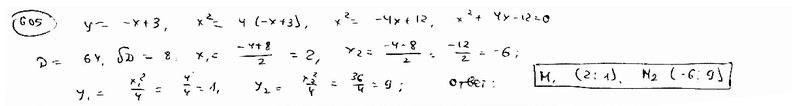
| ||
Определить точки пересечения прямой 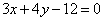 и параболы и параболы 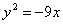 . .
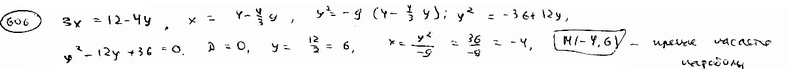
| ||
Определить точки пересечения прямой 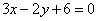 и параболы и параболы 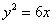 . .
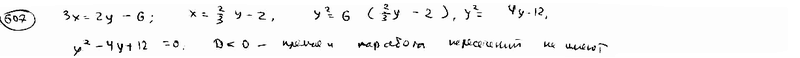
| ||
| В следующих случаях определить, как расположена данная прямая относительно данной параболы – пересекает ли, касается или проходит вне ее: | ||
| 608.1 | 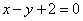 , , 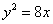 ; ;
| |
| 608.2 | 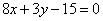 , ,  ; ;
| |
| 608.3 | 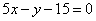 , , 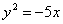 . .
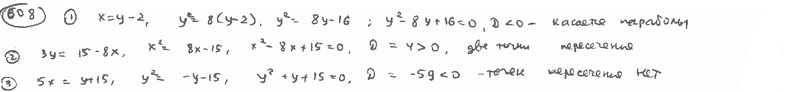
| |
Определить, при каких значениях углового коэффициента k прямая 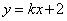 : :
| ||
| 609.1 | пересекает параболу 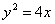 ; ;
| |
| 609.2 | касается ее; | |
| 609.3 | проходит вне этой параболы.

| |
Вывести условие, при котором прямая  касается параболы касается параболы 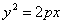 . .
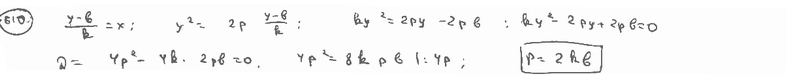
| ||
Доказать, что к параболе 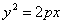 можно провести одну и только одну касательную с угловым коэффициентом можно провести одну и только одну касательную с угловым коэффициентом 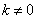 . .
| ||

| ||
Составить уравнение касательной к параболе 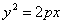 в ее точке М1(x1; y1). в ее точке М1(x1; y1).

| ||
Составить уравнение прямой, которая касается параболы 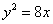 и параллельна прямой и параллельна прямой 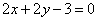 . .
| ||
Составить уравнение прямой, которая касается параболы 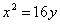 и перпендикулярна к прямой и перпендикулярна к прямой 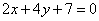 . .

| ||
Провести касательную к параболе 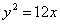 параллельно прямой параллельно прямой 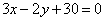 и вычислить расстояние d между этой касательной и данной прямой. и вычислить расстояние d между этой касательной и данной прямой.

| ||
На параболе 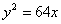 найти точку М1, ближайшую к прямой найти точку М1, ближайшую к прямой 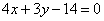 , и вычислить расстояние d от точки М1 до этой прямой. , и вычислить расстояние d от точки М1 до этой прямой.
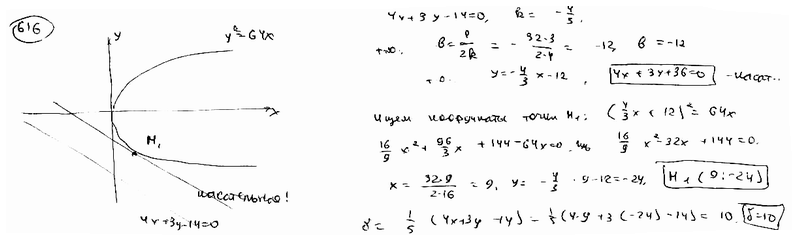
| ||
Составить уравнения касательных к параболе 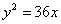 , проведенных из точки А(2; 9). , проведенных из точки А(2; 9).
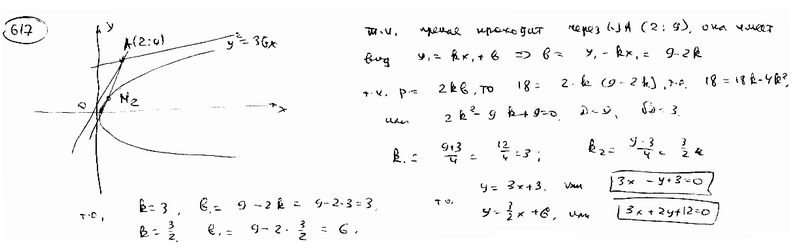
| ||
К параболе 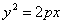 проведена касательная. Доказать, что вершина этой параболы лежит посередине между точкой пересечения касательной с осью Ох и проекцией точки касания на ось Ох. проведена касательная. Доказать, что вершина этой параболы лежит посередине между точкой пересечения касательной с осью Ох и проекцией точки касания на ось Ох.
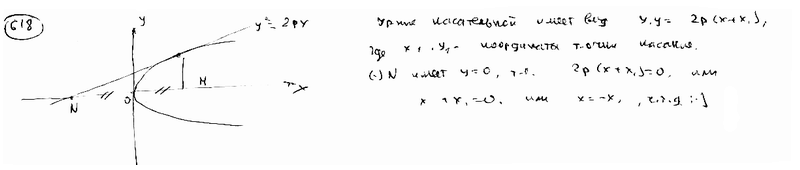
| ||
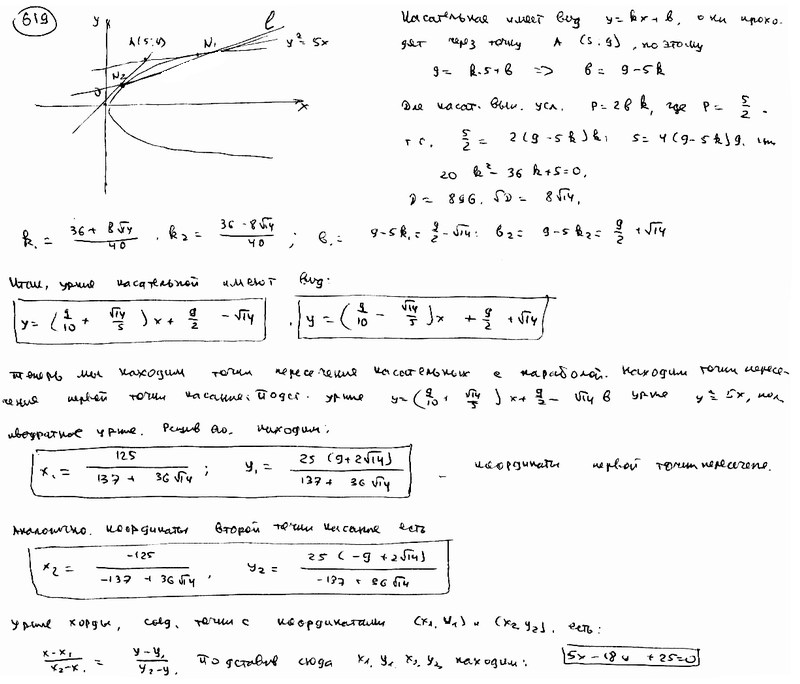
Из точки А(5; 9) проведены касательные к параболе 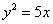 . Составить уравнение хорды, соединяющей точки касания. . Составить уравнение хорды, соединяющей точки касания.
| ||
Из точки Р(-3; 12) проведены касательные к параболе 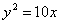 . Вычислить расстояние d от точки Р до хорды параболы, соединяющей точки касания. . Вычислить расстояние d от точки Р до хорды параболы, соединяющей точки касания.

| ||
Определить точки пересечения эллипса 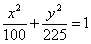 и параболы и параболы 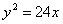 . .

| ||
Определить точки пересечения гиперболы 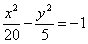 и параболы и параболы  . .

| ||
Определить точки пересечения парабол 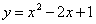 , , 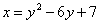 . .

| ||
Доказать, что прямая, касающаяся параболы в некоторой точке М, составляет равные углы с фокальным радиусом точки М и с лучом, который, исходя из М, идет параллельно оси параболы в ту сторону, куда парабола бесконечно простирается.

| ||
Из фокуса параболы 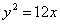 под острым углом под острым углом  к оси Ох направлен луч света. Известно, что к оси Ох направлен луч света. Известно, что 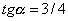 . Дойдя до параболы, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч. . Дойдя до параболы, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.

| ||
Доказать, что две параболы, имеющую общую ось и общий фокус, расположенный между ее вершинами, пересекаются под прямым углом.

| ||
Доказать, что если две параболы со взаимно перпендикулярными осями пересекаются в четырех точках, то эти точки лежат на одной окружности.
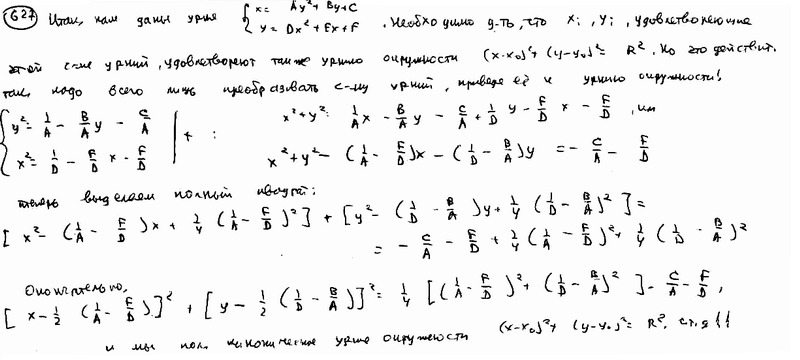
|






