Вывести уравнение геометрического места точек, одинаково удаленных от координатных осей.

| ||
Вывести уравнение геометрического места точек, находящихся на расстоянии а от оси Оу.

| ||
Вывести уравнение геометрического места точек, находящихся на расстоянии b от оси Ох.

| ||
Из точки Р(6; -8) проведены всевозможные лучи до пересечения с осью абсцисс. Составить уравнение геометрического места их середин.

| ||
Из точки С(10; -3) проведены всевозможные лучи до пересечения с осью ординат. Составить уравнение геометрического места их середины.

| ||
| Вывести уравнение траектории точки, которая в каждый момент движения одинаково удалена от точек: | ||
| 179.1 | А(3; 2) и В(2; 3); | |
| 179.2 | А(5; -1) и В(1; -5); | |
| 179.3 | А(5; -2) и В(-3; -2); | |
| 179.4 | А(3; -1) и В(3; 5).

| |
Составить уравнение геометрического места точек, разность квадратов расстояний которых до точек А(-а; 0) и В(а; 0) равна с.
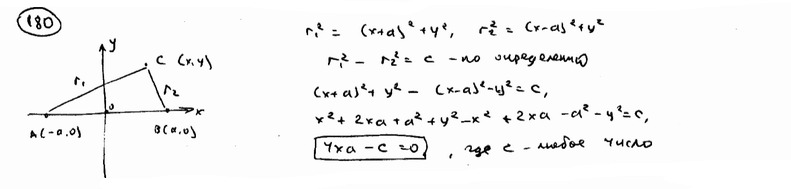
| ||
Вывести уравнение окружности, имеющей центр в начале координат и радиус r.

| ||
Вывести уравнение окружности, имеющей, имеющей центр С( ; ; 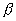 ) и радиус r. ) и радиус r.

| ||
Дано уравнение окружности  . Составить уравнение геометрического места середин тех хорд этой окружности, длина которых равна 8. . Составить уравнение геометрического места середин тех хорд этой окружности, длина которых равна 8.

| ||
Составить уравнение геометрического места точек, сумма квадратов расстояний которых до точек А(-3; 0) и В(3; 0) равна 50.
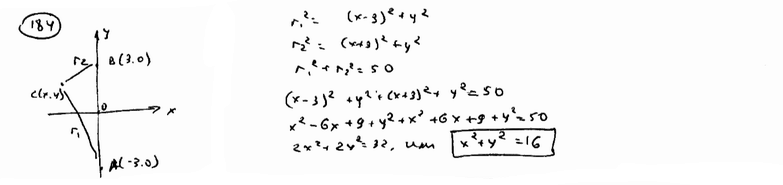
| ||
Ввершины квадрата суть точки А(а; а), В(-а; а), С(-а; -а) и D(а; -а). Составить уравнение геометрического места точек, сумма квадратов расстояний которых до сторон этого квадрата есть величина постоянная, равна 6а2.

| ||
Через начало координат проведены всевозможные хорды окружности  . Составить уравнение геометрического места середин этих хорд. . Составить уравнение геометрического места середин этих хорд.

| ||
Вывести уравнение геометрического места точек, сумма расстояний которых до двух данных точек F1(-3; 0), F2(3; 0) есть величина постоянная, равная 10.
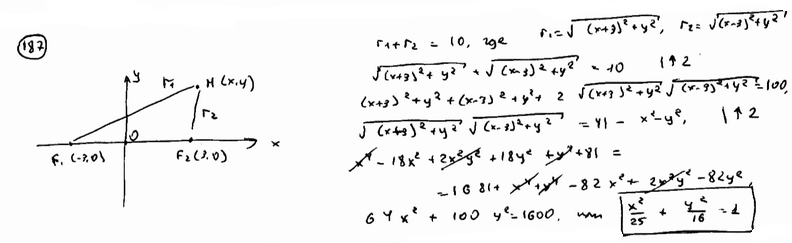
| ||
Вывести уравнение геометрического места точек, разность расстояний которых до двух данных точек F1(-5; 0), F2(5; 0) есть величина постоянная, равная 6.
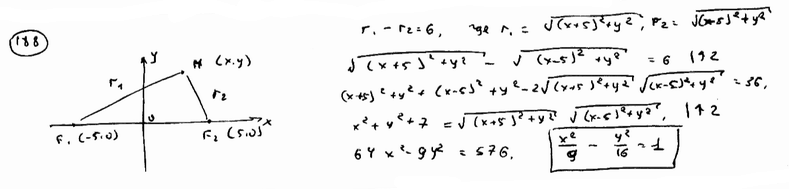
| ||
Вывести уравнение геометрического места точек, для которых расстояние до данной точки F(3; 0) равно расстоянию до данной прямой  . .

| ||
Вывести уравнение геометрического места точек, сумма расстояний которых до двух данных точек F1(-c; 0), F2(c; 0) есть величина постоянная, равная 2а. Это геометрическое место называется эллипсом, точки F1 и F2 – фокусами эллипса. Доказать, что уравнение эллипса имеет вид  , где , где 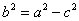 . .

| ||
Вывести уравнение геометрического места точек, разность расстояний которых до двух данных точек F1(-c; 0), F2(c; 0) есть величина постоянная, равная 2а. Это геометрическое место называется гиперболой, точки F1 и F2 – фокусами гиперболы. Доказать, что уравнение гиперболы имеет вид  , где , где 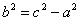 . .

| ||
Вывести уравнение геометрического места точек, для которых расстояние до данной точки F(p/2; 0) равно расстоянию до данной прямой x=-p/2. Это геометрическое место называется параболой, точка F – фокусом параболы, данная прямая – ее директрисой.
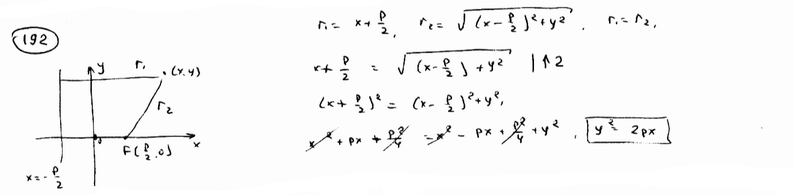
| ||
Вывести уравнение геометрического места точек, для которых отношение расстояния до данной точки F(-4; 0) к расстоянию до данной прямой 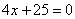 равно 4/5. равно 4/5.

| ||
Вывести уравнение геометрического места точек, для которых отношение расстояния до данной точки F(-5;0) к расстоянию до данной прямой  равно 5/4. равно 5/4.

| ||
Вывести уравнение геометрического места точек, для которых кратчайшие расстояния до двух данных окружностей 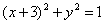 , ,  равны между собой. равны между собой.

| ||
Вывести уравнение геометрического места точек, для которых кратчайшие расстояния до двух данных окружностей  , ,  равны между собой. равны между собой.
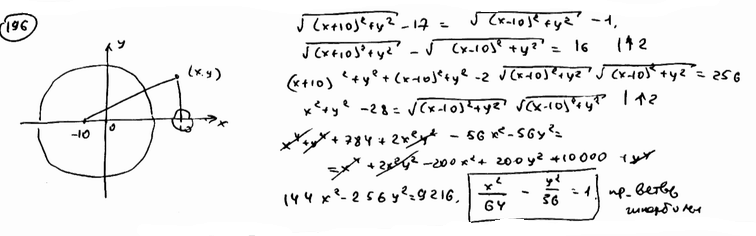
| ||
Вывести уравнение геометрического места точек, для которых кратчайшие расстояния до данной окружности 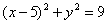 и до данной прямой и до данной прямой  равны между собой. равны между собой.
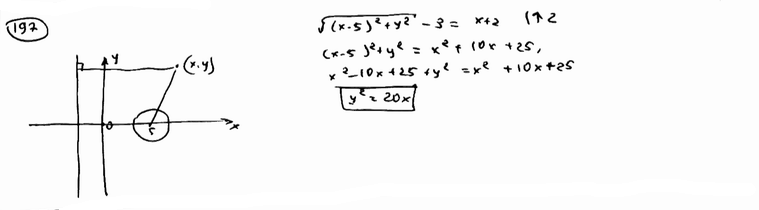
| ||
Прямая перпендикулярна полярной оси и отсекает на ней отрезок, равный 3. Составить уравнение этой прямой в полярных координатах.

| ||
Луч выходит из полюса и наклонен к полярной оси под углом  . Составить уравнение этого луча в полярных координатах. . Составить уравнение этого луча в полярных координатах.

| ||
Прямая проходит через полюс и наклонена к полярной оси под углом 450. Составить уравнение этой прямой в полярных координатах.

| ||
В полярных координатах составить уравнение геометрического места точек, расстояния которых от полярной оси равны 5.

| ||
Окружность радиуса R=5 проходит через полюс, ее центр лежит на полярной оси. Составить уравнение этой окружности в полярной системе координат.
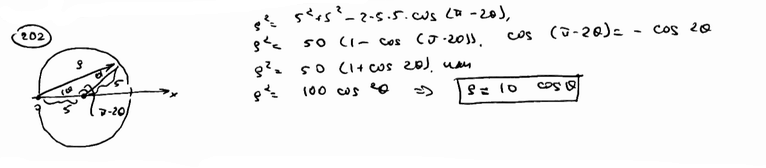
| ||
Окружность радиуса R=3 касается полярной оси в полюсе. Составить уравнение этой окружности в полярной системе координат.

|

Поиск:
Рекомендуем:
 Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ
Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки)
Нейроглия (или проще глия, глиальные клетки)
Категории:
Глава 10. Вывод уравнений заранее данных линий
|
|
|
|
|
|
|
|
|
|
Дата добавления: 2016-10-22; Мы поможем в написании ваших работ!; просмотров: 1465 | Нарушение авторских прав
Поиск на сайте:
Лучшие изречения:

