| Определить, какие из следующих уравнений прямых являются нормальными: | ||
| 309.1 | 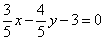 ; ;
| |
| 309.2 | 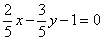 ; ;
| |
| 309.3 | 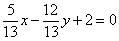 ; ;
| |
| 309.4 | 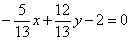 ; ;
| |
| 309.5 | 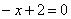 ; ;
| |
| 309.6 |  ; ;
| |
| 309.7 |  ; ;
| |
| 309.8 | 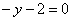 . .

| |
| Привести общее уравнение прямой к нормальному виду в каждом из следующих случаев: | ||
| 310.1 |  ; ;
| |
| 310.2 | 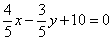 ; ;
| |
| 310.3 | 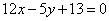 ; ;
| |
| 310.4 |  ; ;
| |
| 310.5 | 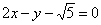 . .
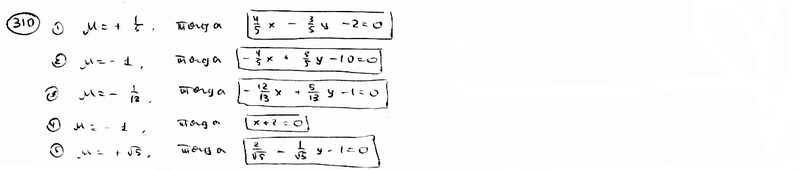
| |
Даны уравнения прямых. Определить полярный угол нормали  и отрезок p для каждой из данных прямых: по полученным значениям параметров и отрезок p для каждой из данных прямых: по полученным значениям параметров  и р построить эти прямые на четеже (в последних двух случаях построение прямой выполнить, считая и р построить эти прямые на четеже (в последних двух случаях построение прямой выполнить, считая 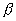 =300 и q=2). =300 и q=2).
| ||
| 311.1 |  ; ;
| |
| 311.2 |  ; ;
| |
| 311.3 |  ; ;
| |
| 311.4 |  ; ;
| |
| 311.5 | 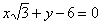 ; ;
| |
| 311.6 | 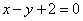 ; ;
| |
| 311.7 | 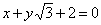 ; ;
| |
| 311.8 | 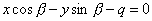 , q>0, , q>0, 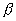 - острый угол. - острый угол.
| |
| 311.9 | 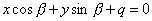 , q>0, , q>0, 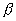 - острый угол. - острый угол.
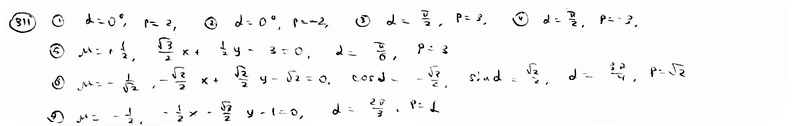
| |
Вычислить величину отклонения  и расстояние d от точки до прямой в каждом из следующих случаев: и расстояние d от точки до прямой в каждом из следующих случаев:
| ||
| 312.1 | A(2; -1), 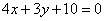 ; ;
| |
| 312.2 | B(0; -3), 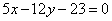 ; ;
| |
| 312.3 | P(-2; 3), 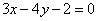 ; ;
| |
| 312.4 | Q(1; -2), 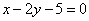 . .

| |
| Установить, лежат ли точка М(1; -3) и начало координат по одну или разные стороны каждой из следующих прямых: | ||
| 313.1 |  ; ;
| |
| 313.2 | 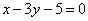 ; ;
| |
| 313.3 |  ; ;
| |
| 313.4 |  ; ;
| |
| 313.5 | 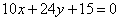 . .
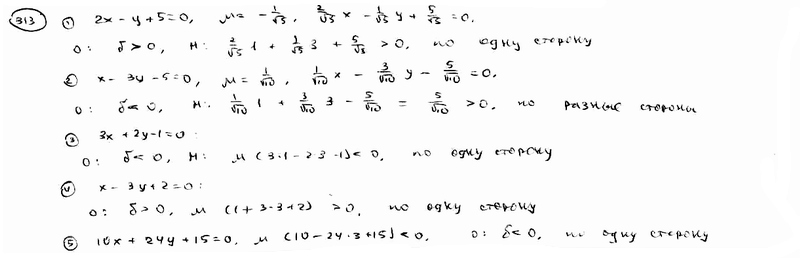
| |
Точка А(2; -5) является вершиной квадрата, одна из сторон которого лежит на прямой  . Вычислить площадь этого квадрата. . Вычислить площадь этого квадрата.
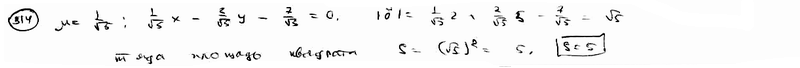
| ||
Даны уравнения двух сторон прямоугольника 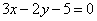 , ,  и одна из его вершин А(-2; 1). Вычислить площадь этого прямоугольника. и одна из его вершин А(-2; 1). Вычислить площадь этого прямоугольника.
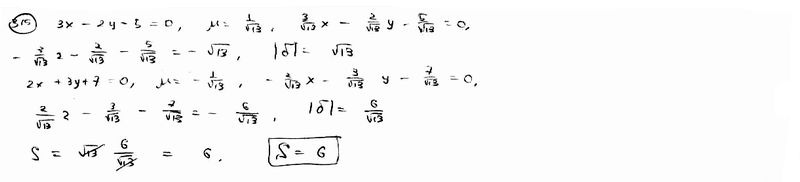
| ||
Доказать, что прямая 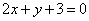 пересекает отрезок, ограниченный точками А(-5; 1), В(3; 7). пересекает отрезок, ограниченный точками А(-5; 1), В(3; 7).
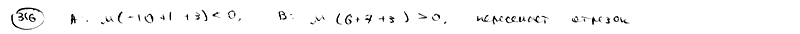
| ||
Доказать, что прямая 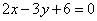 не пересекает отрезка, ограниченного точками M1(-2; -3), M2(1; -2). не пересекает отрезка, ограниченного точками M1(-2; -3), M2(1; -2).
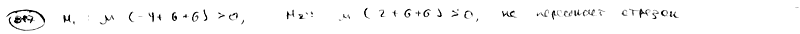
| ||
Последовательные вершины четырехугольника суть точки A(-1; 6), B(-1; -4), C(7; -1), D(2; 9). Установить, является ли этот четырехугольник выпуклым.

| ||
Последовательные вершины четырехугольника суть точки A(-1; 6), B(1; -3), C(4; 10), D(9; 0). Установит, является ли этот четырехугольник выпуклым.

| ||
Даны вершины треугольника A(-10; -13), B(-2; 3), C(2; 1). Вычислить длину перпендикуляра, оущенного из вершины В на медиану, проведенную из вершины С.
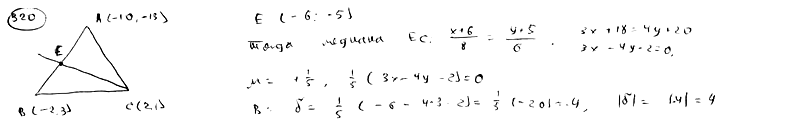
| ||
Стороны АВ, ВС, СА треугольника АВС, соответственно даны уравнениями 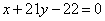 , , 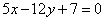 , , 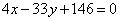 . Вычислить расстояние от центра масс этого треугольника до стороны ВС. . Вычислить расстояние от центра масс этого треугольника до стороны ВС.
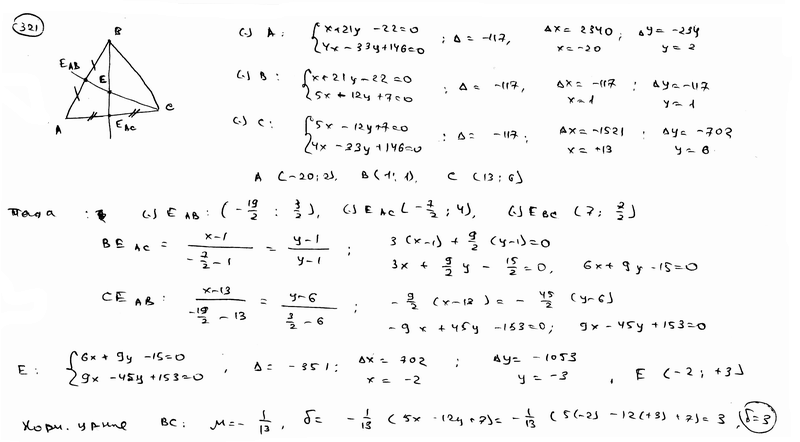
| ||
| Вычислить расстояние d между параллельными прямыми в каждом из следующих случаев: | ||
| 322.1 | 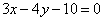 , , 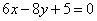 ; ;
| |
| 322.2 | 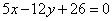 , , 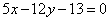 ; ;
| |
| 322.3 | 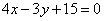 , , 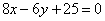 ; ;
| |
| 322.4 | 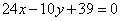 , , 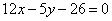 . .
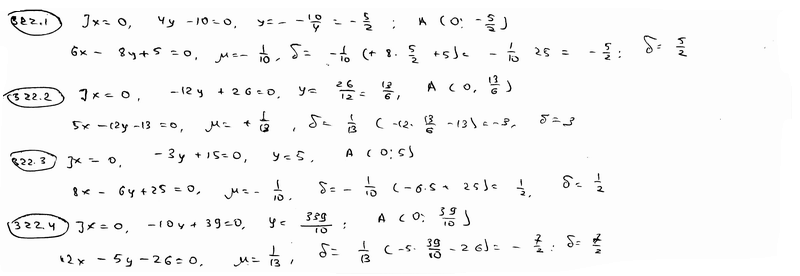
| |
Две стороны квадрата лежат на прямых 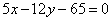 , , 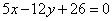 . Вычислить его площадь. . Вычислить его площадь.
| ||
Доказать, что прямая 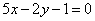 параллельна прямым параллельна прямым 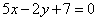 , , 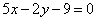 и делит расстояние между ними пополам. и делит расстояние между ними пополам.
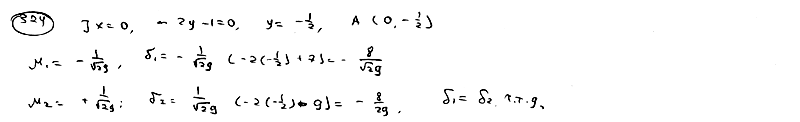
| ||
Даны параллельные прямые 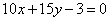 , ,  , ,  . Установить, что первая из них лежит между двумя другими, и вычислить отношение, в котором она делит расстояние между ними. . Установить, что первая из них лежит между двумя другими, и вычислить отношение, в котором она делит расстояние между ними.
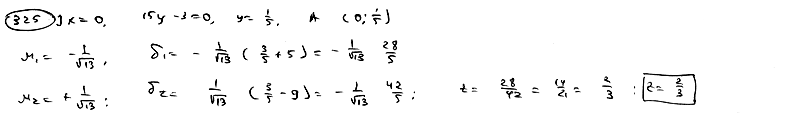
| ||
Доказать, что через точку Р(2; 7) можно провести две прямые так, чтобы их расстояния от точки Q(1; 2) были равны 5. Составить уравнения этих прямых.

| ||
Доказать, что через точку Р(2; 5) можно провести две прямые так, чтобы их расстояния от точки Q(5; 1) были равны 3. Составить уравнения этих прямых.

| ||
Доказать, что через точку С(7; -2) можно провести только одну прямую так, чтобы расстояние ее от точки А(4; -6) было равно 5. Составить ее уравнение.
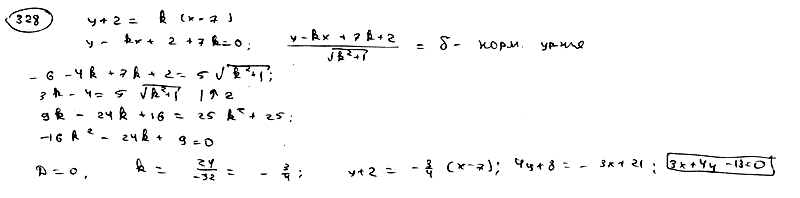
| ||
Доказать, что через точку В(4; -5) невозможно провести прямую, чтобы расстояние от точки С(-2; 3) было равно 12.
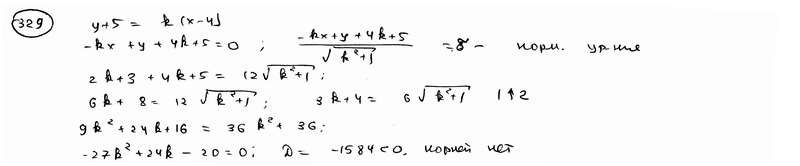
| ||
Вывести уравнение геометрического места точек, отклонение которых от прямых 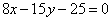 равно –2. равно –2.

| ||
Составить уравнение прямых, параллельных прямой 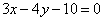 и отстоящие от нее на расстояние d=3. и отстоящие от нее на расстояние d=3.
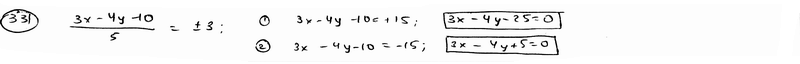
| ||
Даны две смежные вершины квадрата А(2; 0) и В(-1; 4). Составить уравнения его сторон.

| ||
Точка А(5; -1) является вершиной квадрата, одна из сторон которого лежит на прямой 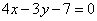 . Составить уравнения прямых, на которых лежат остальные стороны этого квадрата. . Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.

| ||
Даны уравнения двух сторон квадрата 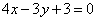 , , 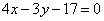 и одна из его вершин А(2; -3). Составить уравнения двух других сторон этого квадрата. и одна из его вершин А(2; -3). Составить уравнения двух других сторон этого квадрата.
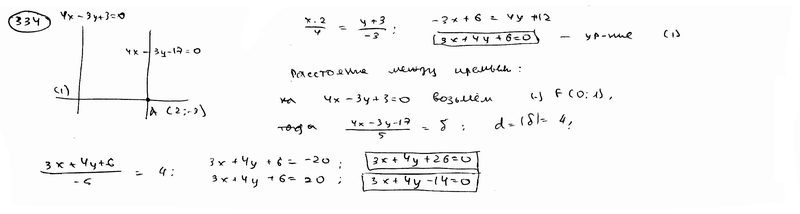
| ||
Даны уравнения двух сторон квадрата 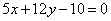 , , 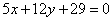 . Составить уравнения двух других его сторон при условии, что точка M1(-3; 5) лежит на стороне этого квадрата. . Составить уравнения двух других его сторон при условии, что точка M1(-3; 5) лежит на стороне этого квадрата.
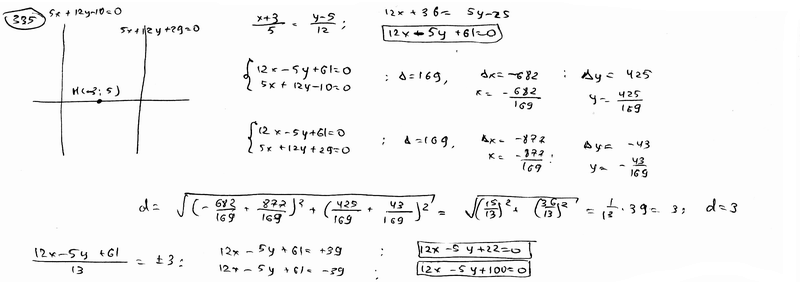
| ||
Отклонения точки М от прямых 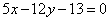 , , 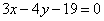 равны соответственно –3 и –5. Определить координаты точки М. равны соответственно –3 и –5. Определить координаты точки М.
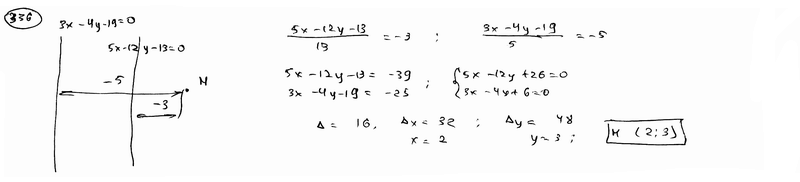
| ||
| Составить уравнение прямой, проходящей через точку Р(-2; 3) на одинаковых расстояниях от точек А(5; -1) и В(3; 7). | ||
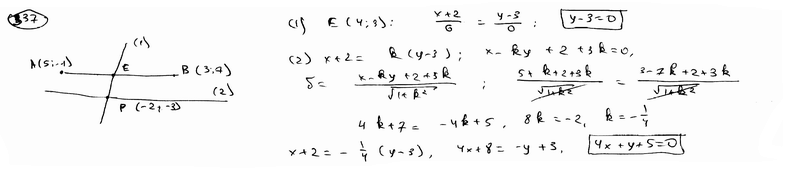
| ||
| Составить уравнения биссектрис углов, образованных двумя пересекающимися прямыми: | ||
| 338.1 | 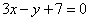 , , 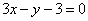 ; ;
| |
| 338.2 | 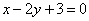 , , 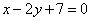 ; ;
| |
| 338.3 | 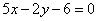 , , 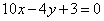 ; ;
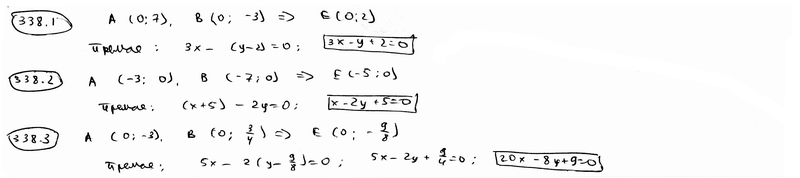
| |
| Составить уравнения биссектрис углов, образованных двумя пересекающимися прямыми: | ||
| 339.1 | 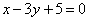 , , 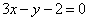 ; ;
| |
| 339.2 |  , , 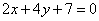 ; ;
| |
| 339.3 |  , , 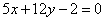 . .

| |
Составить уравнения прямых, которые проходят через точку Р(2; -1) и вместе с прямыми  , , 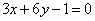 образуют равнобедренные треугольники. образуют равнобедренные треугольники.

| ||
| Определить, лежат ли точки М(1; -2) и начало координат в одном, в смежных или вертикальных углах, образованных при пересечении двух прямых: | ||
| 341.1 |  , , 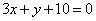 ; ;
| |
| 341.2 | 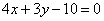 , , 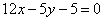 ; ;
| |
| 341.3 |  , , 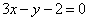 . .
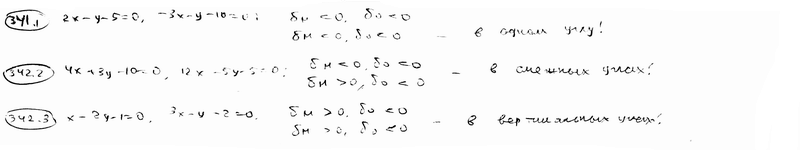
| |
| Определить, лежат ли точки М(2; 3) и N(5; -1) в одном, в смежных или вертикальных углах, образованных при пересечении двух прямых: | ||
| 342.1 | 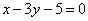 , , 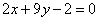 ; ;
| |
| 342.2 | 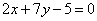 , , 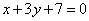 ; ;
| |
| 342.3 | 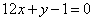 , , 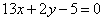 . .

| |
Определить, лежит ли начало координат внутри или вне треугольника, стороны которого даны уравнениями  , , 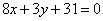 , , 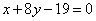 . .

| ||
Определить, лежит ли точка М(-3; 2) внутри или вне треугольника стороны которого даны уравнениями 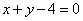 , , 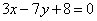 , , 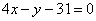 . .

| ||
Определить, какой из углов, острый или тупой, образованных двумя прямыми  , , 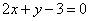 содержит начало координат. содержит начало координат.
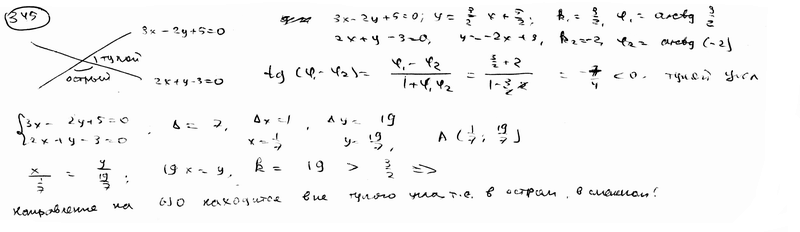
| ||
Определить, какой из углов, острый или тупой, образованный двумя прямыми 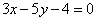 , ,  , содержит точку М(2; -5). , содержит точку М(2; -5).
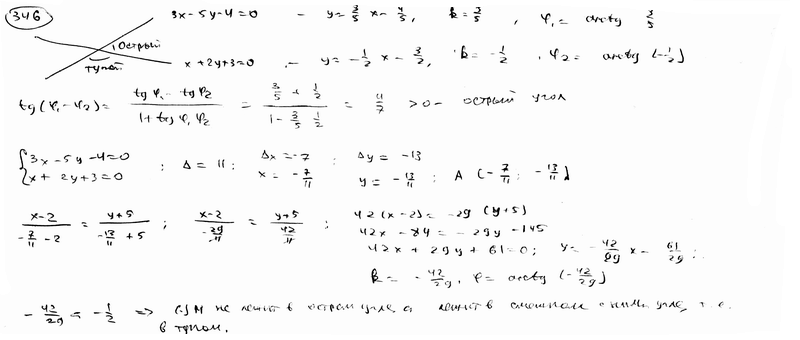
| ||
Составить уравнение биссектрисы угла между прямыми 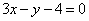 , , 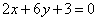 , в котором лежит начало координат. , в котором лежит начало координат.
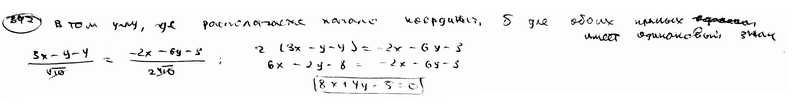
| ||
Составить уравнение биссектрисы угла между прямыми 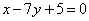 , , 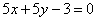 , смежного с углом, содержащего начало координат. , смежного с углом, содержащего начало координат.
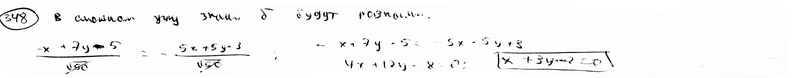
| ||
Составить уравнение биссектрисы угла между прямыми 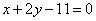 , , 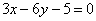 , в котором лежит точка М(1; -3). , в котором лежит точка М(1; -3).

| ||
Составить уравнение биссектрисы угла между прямыми 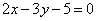 , , 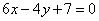 , смежного с углом, содержащим точку С(2; -1). , смежного с углом, содержащим точку С(2; -1).

| ||
Составить уравнение биссектрисы острого угла, образованного двумя прямыми 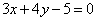 , , 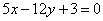 . .
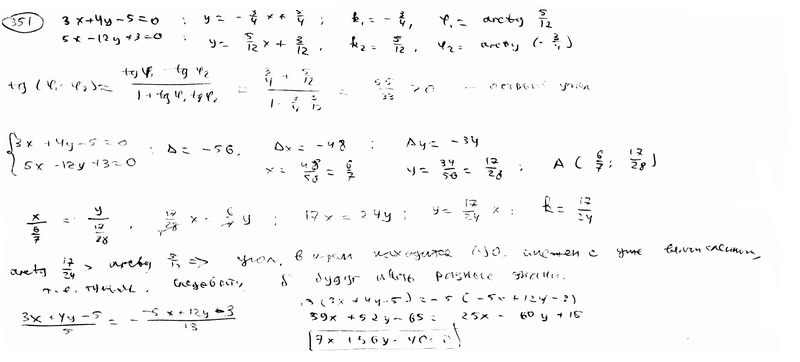
| ||
Составить уравнение биссектрисы тупого угла, образованного двумя прямыми 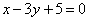 , , 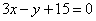 . .
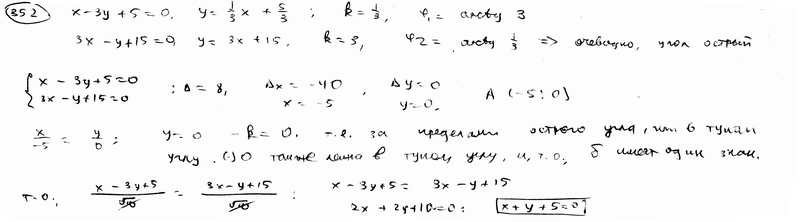
|

Поиск:
Рекомендуем:
 Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ
Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки)
Нейроглия (или проще глия, глиальные клетки)
Категории:
Глава 14. Нормальное уравнение прямой. Расстояние от точки до прямой
|
|
|
|
|
|
|
|
|
|
Дата добавления: 2016-10-22; Мы поможем в написании ваших работ!; просмотров: 1819 | Нарушение авторских прав
Поиск на сайте:
Лучшие изречения:

