Глава 22. Диаметры линий второго порядка

		Составить уравнение диаметра эллипса , проходящего через середину его хорды, отсекаемой на прямой .
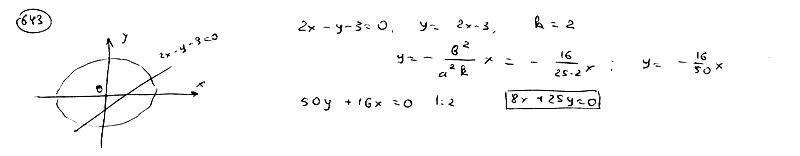
		Составить уравнение хорды эллипса , проходящей через точку А(1; -2) и делящейся ею пополам.
		Составить уравнения двух взаимно сопряженных диаметров эллипса , из которых один образует с осью Ох угол 45⁰.
		Составить уравнения двух взаимно двух взаимно сопряженных диаметров эллипса , из которых один параллелен прямой .
		Составить уравнения двух взаимно сопряженных диаметров эллипса , из которых один перпендикулярен к прямой .
		На чертеже изображен эллипс. Пользуясь циркулем и линейкой, построить его центр.
		Доказать, что оси эллипса являются единственной парой его главных диаметров.
		Пользуясь свойствами сопряженных диаметров, доказать, что каждый диаметр окружности является главным.
		а). В эллипс вписан равнобедренный треугольник так, что его вершина совпадает с одной из вершин эллипса. Доказать, что основание этого треугольника параллельно одной из осей эллипса; б). Доказать, что стороны прямоугольника вписанного в эллипс,параллельны осям этого эллипса; в). На чертеже изображен эллипс. Пользуясь циркулем и линейкой, построить его главные диаметры.
		Доказать, что хорды эллипса, соединяющие его произвольную произвольную точку с концами любого диаметра этого эллипса, праллельны паре его сопряженных диаметров.
		а). Доказать, что сумма квадратов двух сопряженных полудиаметров эллипса есть величина постоянная (равная сумме квадратов его полуосей), б). Доказать, что площадь параллелограмма, построенного на двух сопряженных полудиаметрах эллипса, есть величина постоянная (равная площади прямоугольника, построенного на его полуосях).
		Составить уравнение диаметра гиперболы 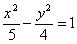, походящего через середину ее хорды, отсекаемой на прямой .
		Дана гипербола . Составить уравнение ее хорды, которая проходит через точку А(3; -1) и делится точкой А пополам.
		Составить уравнениядвух сопряженных диаметров гиперболы , из которых один проходит через точку А(8; 1).
		Составить уравнения сопряженных диаметров гиперболы , угол между которыми равен 45⁰.
		На чертеже изображена гипербола. Пользуясь циркулем и линейкой, построить ее центр.
		Доказать, что оси гиперболы являются единственной парой ее главных диаметров.
		На чертеже изображена гипербола. Пользуясь циркулем и линейкой, построить ее главные диаметры.
		Составить уравнение диаметра параболы 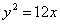, проходящего через середину ее хорды, отсекаемой на прямой .
		Дана парабола 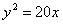. Составить уравнение ее хорды, которая проходит через точку А(2; 5) и делится точкой А пополам.
		Доказать, что ось параболы является единственной ее главным диаметром.
		На чертеже изображена парабола. Пользуясь циркулем и линейкой, построить ее главный диаметр.