Найти центр пучка прямых, данного уравнением  . .

| ||
Найти уравнение прямой, принадлежащей пучку прямых  и и
| ||
| 354.1 | Проходящей через точку А(3; -1); | |
| 354.2 | Проходящей через начало координат; | |
| 354.3 | Параллельной оси Ox; | |
| 354.4 | Параллельной оси Oy; | |
| 354.5 | Параллельной прямой  ; ;
| |
| 354.6 | Перпендикулярной к прямой  . .

| |
Составить уравнение прямой, проходящей через точку пересечения прямых  , ,  и отсекающий на оси ординат отрезок b=-3. Решить задачу, не определяя координат точки пересечения данных прямых. и отсекающий на оси ординат отрезок b=-3. Решить задачу, не определяя координат точки пересечения данных прямых.

| ||
Составить уравнение прямой, которая проходит через точку пересечения прямых  , ,  и делит пополам отрезок, ограниченный точками M1(5; -6), M2(-1; -4). Решить задачу, не вычисляя координат точки пересечения данных прямых. и делит пополам отрезок, ограниченный точками M1(5; -6), M2(-1; -4). Решить задачу, не вычисляя координат точки пересечения данных прямых.

| ||
Дано уравнение пучка прямых  . Написать уравнение прямой этого пучка, проходящей через центр масс однородной треугольной пластинки, вершины которой суть точки A(-1; 2), B(4; -4), C(6; -1). . Написать уравнение прямой этого пучка, проходящей через центр масс однородной треугольной пластинки, вершины которой суть точки A(-1; 2), B(4; -4), C(6; -1).

| ||
Дано уравнение пучка прямых  . Найти прямую этого пука, проходящую через середину отрезка прямой . Найти прямую этого пука, проходящую через середину отрезка прямой  , заключенного между прямыми , заключенного между прямыми  , ,  . .

| ||
Даны уравнения сторон треугольника  , ,  , ,  . Не определяя координат его вершин, составить уравнения высот этого трегоульника. . Не определяя координат его вершин, составить уравнения высот этого трегоульника.
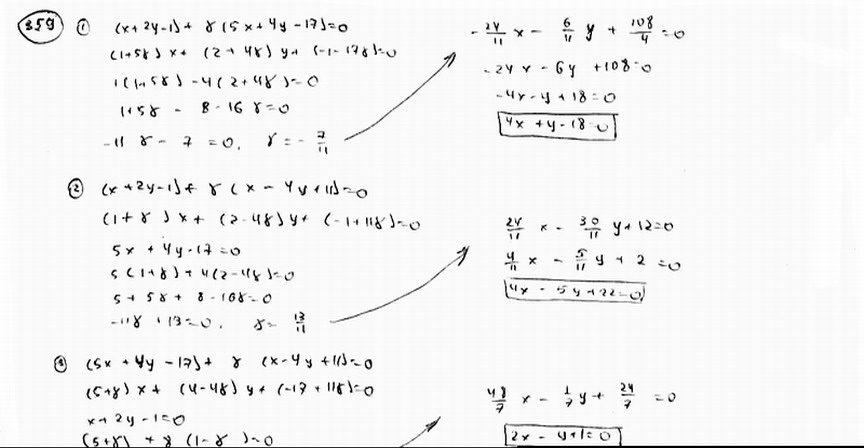 (ВНИМАНИЕ. ИЗОБРАЖЕНИЕ РЕШЕНИЯ ОБРЕЗАНО ВНИЗУ. РЕШЕНИЕ НЕ ПОЛНОЕ).
(ВНИМАНИЕ. ИЗОБРАЖЕНИЕ РЕШЕНИЯ ОБРЕЗАНО ВНИЗУ. РЕШЕНИЕ НЕ ПОЛНОЕ).
| ||
Составить уравнение прямой, проходящей через точку пересечения прямых  , ,  под углом 450 к прямой под углом 450 к прямой  . Решить задачу, не вычисляя координат точки пересечения данных прямых. . Решить задачу, не вычисляя координат точки пересечения данных прямых.

| ||
В треугольнике АВС даны уравнения высоты AN:  , высоты BN: , высоты BN:  и стороны АВ: и стороны АВ:  . Не определяя координат вершин и точки пересечения высот треугольника, составить уравнение двух других сторон и третьей высоты. . Не определяя координат вершин и точки пересечения высот треугольника, составить уравнение двух других сторон и третьей высоты.

| ||
Составить уравнения сторон треугольника АВС, зная одну его вершину А(2; -1), а также уравнения высоты  и биссектрисы и биссектрисы  , проведенных из одной вершины. Решить задачу, не вычисляя координат вершин В и С. , проведенных из одной вершины. Решить задачу, не вычисляя координат вершин В и С.

| ||
Дано уравнение пучка прямых  . Найти прямые этого пучка, отрезки которых, заключенные между прямыми . Найти прямые этого пучка, отрезки которых, заключенные между прямыми  , ,  , равны , равны  . .

| ||
Дано уравнение пучка прямых  . Доказать, что прямая . Доказать, что прямая  принадлежит этому пучку. принадлежит этому пучку.

| ||
Дано уравнение пучка прямых  . Доказать, что прямая . Доказать, что прямая  не принадлежит этому пучку. не принадлежит этому пучку.

| ||
Дано уравнение пучка прямых  . Найти, при каком значении С прямая . Найти, при каком значении С прямая  будет принадлежать этому пучку. будет принадлежать этому пучку.

| ||
Дано уравнение пучка прямых  . Найти, при каких значениях a прямая . Найти, при каких значениях a прямая  не будет принадлежать этому пучку. не будет принадлежать этому пучку.

| ||
Центр пучка прямых  является вершиной квадрата, диагональ которого лежит на прямой является вершиной квадрата, диагональ которого лежит на прямой  . Составить уравнения сторон и второй диагонали этого квадрата. . Составить уравнения сторон и второй диагонали этого квадрата.

| ||
Дано уравнение пучка прямых  . Найти прямую этого пучка, отсекающую на координатных осях отличные от нуля отрезки равной величины (считая от начала координат). . Найти прямую этого пучка, отсекающую на координатных осях отличные от нуля отрезки равной величины (считая от начала координат).

| ||
Дано уравнение пучка прямых  . Найти прямые этого пучка, отсекающие на координатных осях отрезки равной длины (считая от начала координат). . Найти прямые этого пучка, отсекающие на координатных осях отрезки равной длины (считая от начала координат).

| ||
Дано уравнение пучка прямых  . Найти прямые этого пучка, отсекающие от координатных углов треугольники с площадью, равной 9. . Найти прямые этого пучка, отсекающие от координатных углов треугольники с площадью, равной 9.

| ||
Дано уравнение пучка прямых  . Доказать, что среди прямых этого пучка существует только одна прямая, отстоящая от точки Р(2; -3) на расстояние . Доказать, что среди прямых этого пучка существует только одна прямая, отстоящая от точки Р(2; -3) на расстояние  . Написать уравнение этой прямой. . Написать уравнение этой прямой.

| ||
Дано уравнение пучка прямых  . Доказать, что среди прямых этого пучка нет прямой, отстоящей от точки Р(3; -1) на расстояние d=3. . Доказать, что среди прямых этого пучка нет прямой, отстоящей от точки Р(3; -1) на расстояние d=3.

| ||
Составить уравнение прямой, проходящей через точку пересечения прямых  , ,  и отстоящей от точки С(-1; 2) на расстояние d=5. Решить задачу, не вычисляя точки пересечения даных прямых. и отстоящей от точки С(-1; 2) на расстояние d=5. Решить задачу, не вычисляя точки пересечения даных прямых.

| ||
Дано уравнение пучка прямых  . Написать уравнения прямых этого пучка, которые вместе с прямыми . Написать уравнения прямых этого пучка, которые вместе с прямыми  , ,  образуют равнобедренные треугольники. образуют равнобедренные треугольники.

| ||
Составить уравнение прямой, которая проходит через точку пересечения прямых 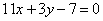 , ,  на одинаковых расстояниях от точек А(3; -2) и В(-1; 6). Решить задачу, не вычисляя координат точки пересечения данных прямых. на одинаковых расстояниях от точек А(3; -2) и В(-1; 6). Решить задачу, не вычисляя координат точки пересечения данных прямых.

| ||
Даны уравнения двух пучков прямых  , ,  . Не определяя их центров, составить уравнение прямой, принадлежащей обоим пучкам. . Не определяя их центров, составить уравнение прямой, принадлежащей обоим пучкам.

| ||
Стороны АВ, ВС, CD, DA четырехугольника ABCD заданы соответственно уравнениями  , ,  , ,  , ,  . Не определяя координат вершин этого четырехугольника, составить уравнения его диагоналей AC и BD. . Не определяя координат вершин этого четырехугольника, составить уравнения его диагоналей AC и BD.

| ||
Центр пучка прямых  является одной из вершин треугольника, две высоты которого даны уравнениями является одной из вершин треугольника, две высоты которого даны уравнениями  , ,  . Составить уравнения сторон этого треугольника. . Составить уравнения сторон этого треугольника.

|

Поиск:
Рекомендуем:
 Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ
Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки)
Нейроглия (или проще глия, глиальные клетки)
Категории:
Глава 15. Уравнение пучка прямых
|
|
|
|
|
|
|
|
|
|
Дата добавления: 2016-10-22; Мы поможем в написании ваших работ!; просмотров: 1228 | Нарушение авторских прав
Поиск на сайте:
Лучшие изречения:

