Даны две функции P и Q, расстояние между которыми равно а, и функция  , где d 1=MP и d 2=MQ. Определить выражение этой функции, если в качестве начала координат принята точка P, а ось Ох направлена по отрезку PQ. , где d 1=MP и d 2=MQ. Определить выражение этой функции, если в качестве начала координат принята точка P, а ось Ох направлена по отрезку PQ.

| ||
| При условиях задачи 146 определить выражение функции f (M) (непосредственно и при помощи преобразования координат, используя результат задачи 146), если: | ||
| 147.1 | Начало координат выбрано в середине отрезка PQ, ось Ох направлена по отрезку PQ. | |
| 147.2 | Начало координат выбрано в точке Р, а ось Ох направлена по отрезку QP.

| |
Даны квадрат ABCD со стороной a и функция  , где d 1=MA, d 2=MB, d 3=MC, d 4=MD. Определить выражение этой функции, если за оси координат приняты диагонали квадрата (причем ось Ох направлена по отрезку АС, ось Оу – по отрезку BD). , где d 1=MA, d 2=MB, d 3=MC, d 4=MD. Определить выражение этой функции, если за оси координат приняты диагонали квадрата (причем ось Ох направлена по отрезку АС, ось Оу – по отрезку BD).

| ||
При условиях задачи 148 определить выражение для f (M) (непосредственно и при помощи преобразования координат, используя результат задачи 148), если начало координат выбрано в точке А, а оси координат направлены по его сторонам (ось Ох – по отрезку АВ, ось Оу – по отрезку AD).

| ||
Дана функция f (x, y)= x 2+ y 2+6 x +8 y. Определить выражение этой функции в новой системе координат, если начало координат перенесено (без изенения направления осей) в точку О’ (3; –4).

| ||
Дана функция f (x, y)= x 2– y 2–16. Определить выражение этой функции в новой системе координат, если координатные оси повернуты на угол –45°.

| ||
Дана функция f (x, y)= x 2+ y 2. Определить выражение этой функции в новой системе координат, если координатные оси повернуты на некоторый угол a.

| ||
Найти такую точку, чтобы при переносе в нее начала координат выражение функции f (x, y)= x 2–4 y 2–6 x +8 y +3=0 после преобразования не содержало членов первой степени относительно новых переменных.
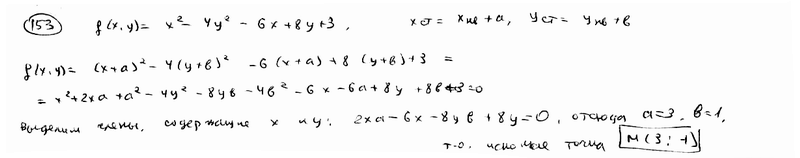
| ||
Найти такую точку, чтобы при переносе в нее начала координат выражение функции f (x, y)== x 2–4 xy +4 y 2+2 x + y –7 не содержало членов первой степени относительно новых переменных.

| ||
На какой угол нужно повернуть координатные оси, чтобы выражение функции f (x, y)== x 2–2 xy + y 2+6 x +3 после преобразования не содержало члена с произведением новых переменных?

| ||
На какой угол нужно повернуть координатные оси, чтобы выражение функции  после преобразования не содержало члена с произведением новых переменных? после преобразования не содержало члена с произведением новых переменных?

|

Поиск:
Рекомендуем:
 Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ
Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки)
Нейроглия (или проще глия, глиальные клетки)
Категории:
Глава 8. Функция двух переменных
|
|
|
|
 , и какие не лежат на ней. Какая линия определена данным уравнением? (Изобразить ее на чертеже).
, и какие не лежат на ней. Какая линия определена данным уравнением? (Изобразить ее на чертеже).

 , найти точки, абсциссы которых равны следующим числам: 1). 0; 2). –3; 3). 5; 4). 7; на этой же линии найти точки, ординаты которых равны следующим числам: 5). 3; 6). –5; 7). –8. Какая линия определена данным уравнением? (Изобразить ее на чертеже).
, найти точки, абсциссы которых равны следующим числам: 1). 0; 2). –3; 3). 5; 4). 7; на этой же линии найти точки, ординаты которых равны следующим числам: 5). 3; 6). –5; 7). –8. Какая линия определена данным уравнением? (Изобразить ее на чертеже).

 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.

 ;
;
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.

 ,
,  ,
,  ,
,  ,
,  .
.

 /3), М2(2; 0), М3(2,
/3), М2(2; 0), М3(2, 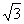 ;
;  , и какие не лежат на ней. Какая линия определяется данным уравнением? (Изобразить ее на чертеже).
, и какие не лежат на ней. Какая линия определяется данным уравнением? (Изобразить ее на чертеже).

 , найти точки, полярные углы которых равны следующим числам: а).
, найти точки, полярные углы которых равны следующим числам: а).  , б).
, б).  ; в). 0; г).
; в). 0; г).  . Какая линия определена данным уравнением: (Построить ее на чертеже).
. Какая линия определена данным уравнением: (Построить ее на чертеже).

 , найти точки, полярные радиусы которых равны следующим числам: а). 1; б). 2; в).
, найти точки, полярные радиусы которых равны следующим числам: а). 1; б). 2; в).  . Какая линия определена данным уравнением? (Построить ее на чертеже).
. Какая линия определена данным уравнением? (Построить ее на чертеже).

 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.

 ;
;
 ;
;
 ;
;
 .
.

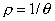 ;
;
 ;
;
 .
.

 ;
;
 .
.

 луч, выходящий из полюса и наклоненный к полярной оси под углом
луч, выходящий из полюса и наклоненный к полярной оси под углом  . Сделать чертеж.
. Сделать чертеж.

 взята точка С, полярный радиус которой равен 47. Определить, на сколько частей эта спираль рассекает полярный радиус точки С. Сделать чертеж.
взята точка С, полярный радиус которой равен 47. Определить, на сколько частей эта спираль рассекает полярный радиус точки С. Сделать чертеж.

 найти точку Р, полярный радиус которой равен 12. Сделать чертеж.
найти точку Р, полярный радиус которой равен 12. Сделать чертеж.

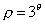 найти точку Q, полярный радиус которой равен 81. Сделать чертеж.
найти точку Q, полярный радиус которой равен 81. Сделать чертеж.


