| 44 | Вычислить проекцию отрезка на ось u, если даны его длина d и угол j наклона к оси: | |||||
| 44.1 | d=6, j =p /3; | |||||
| 44.2 | d=6, j =2p /3; | |||||
| 44.3 | d=7, j =p /2; | |||||
| 44.4 | d=5, j =0; | |||||
| 44.5 | d=5, j =p; | |||||
| 44.6 | d=4, j = -p /3.

| |||||
| 45 | Построить на чертеже отрезки, исходящие из начала координат, зная их проекции на координатные оси: | |||||
| 45.1 | X=3, Y=2; | |||||
| 45.2 | X=2, Y=-5; | |||||
| 45.3 | X=-5, Y=0; | |||||
| 45.4 | X=-2, Y=3; | |||||
| 45.5 | X=0, Y=3; | |||||
| 45.6 | X=-5, Y=-1;

| |||||
| 46 | Построить на чертеже отрезки, имеющие началом точку M(2; -1), зная их проекции на координатные оси: | |||||
| 46.1 | X=4. Y=3; | |||||
| 46.2 | X=2, Y=0; | |||||
| 46.3 | X=-3, Y=1; | |||||
| 46.4 | X=-4, Y=-2; | |||||
| 46.5 | X=0, Y=-3; | |||||
| 46.6 | X=1, Y=-3.

| |||||
| 47 | Даны точки М1(1; -2), М2(2; 1), М3(5; 0), М4(-1; 4), М5(0; -3). Найти проекции на координатные оси следующих отрезков: | |||||
| 47.1 | 
| |||||
| 47.2 | 
| |||||
| 47.3 | 
| |||||
| 47.4 | 

| |||||
| 48 | Даны проекции X=5, Y=-5 отрезка 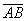 на координатные оси;
зная, что его начало в точке М1(-2; 3), найти координаты его конца. на координатные оси;
зная, что его начало в точке М1(-2; 3), найти координаты его конца.

| |||||
| 49 |
Даны проекции X=4, Y=-5 отрезка 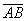 на координатные оси;
зная, что его конец в точке B(1; -3), найти координаты его начала. на координатные оси;
зная, что его конец в точке B(1; -3), найти координаты его начала.

| |||||
| 50 | Построить на чертеже отрезки, исходящие оиз начала координат, зная длину d и полярный угол q каждого из них: | |||||
| 50.1 | d=5, q =p /5; | |||||
| 50.2 | d=3, q =5p /6; | |||||
| 50.3 | d=4, q =-p /3; | |||||
| 50.4 | d=3, q =-4p /3.

| |||||
| 51 | Построить на чертеже отрезки, имеющие началом точку М(2; 3), зная длину и полярный угол каждого из них (координаты точки М декартовы): | |||||
| 51.1 | d=2, q =-p /10; | |||||
| 51.2 | d=1, q =p /9; | |||||
| 51.3 | d=5, q =-p /2ж

| |||||
| 52 | Вычислить проекции на координатные оси отрезков, зная длину d и полярный угол q каждого из них: | |||||
| 52.1 | d=12, q =2p /3; | |||||
| 52.2 | d=6, q =-p /6; | |||||
| 52.3 | d=2, q =-p /4.

| |||||
| 53 | Даны проекции отрезков на координатные оси. Вычислить длину каждого из них. | |||||
| 53.1 | X=3, Y=-4; | |||||
| 53.2 | X=12, Y=5; | |||||
| 53.3 | X=-8, Y=6.

| |||||
| 54 | Даны проекции отрезков на координатные оси. Вычислить длину d и полярный угол q каждого из них. | |||||
| 54.1 | X=1, Y= 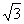 ; ;
| |||||
| 54.2 | X=  , Y= , Y=  ; ;
| |||||
| 54.3 | X=  , Y=2. , Y=2.

| |||||
| 55 | Даны точки М1(2; -3), M2(1; -4), M3(-1; -7), M4(-4; 8). Вычислить длину и полярный угол слдующих отрезков: | |||||
| 55.1 | 
| |||||
| 55.2 | 
| |||||
| 55.3 | 
| |||||
| 55.4 | 

| |||||
| 56 | Длина d отрезка равна 5, его проекция на ось абсцисс равна 4. Найти проекцию этого отрезка на ось ординат при условии, что он образует с осью ординат: | |||||
| 56.1 | Острый угол; | |||||
| 56.2 | Тупой угол.

| |||||
| 57 | Длина отрезка  равна 13; его начало в точке М(3; -2),
проекция на ось абсцисс равна –12.
Найти координаты конца этого отрезка при условии, что он образует с осью ординат: равна 13; его начало в точке М(3; -2),
проекция на ось абсцисс равна –12.
Найти координаты конца этого отрезка при условии, что он образует с осью ординат:
| |||||
| 57.1 | Острый угол; | |||||
| 57.2 | Тупой угол.

| |||||
| 58 | Длина отрезка  равна 17, его конец в точке N(-7; 3),
проекция на ось ординат равна 15.
Найти координаты начала этого отрезка при условии, что он образует с осью абсцисс: равна 17, его конец в точке N(-7; 3),
проекция на ось ординат равна 15.
Найти координаты начала этого отрезка при условии, что он образует с осью абсцисс:
| |||||
| 58.1 | Острый угол; | |||||
| 58.2 | Тупой угол.

| |||||
| 59 | Зная проекции X=1, Y=  отрезка на координатные оси,
найти его проекцию на ось, которая составляет с осью Ox угол q =2p /3. отрезка на координатные оси,
найти его проекцию на ось, которая составляет с осью Ox угол q =2p /3.

| |||||
| 60 |
Даны две точки M1(1; -5), M2(4; -1).
Найти проекцию отрезка  на ось, которая составляет с осью Ox угол q =-p /6. на ось, которая составляет с осью Ox угол q =-p /6.
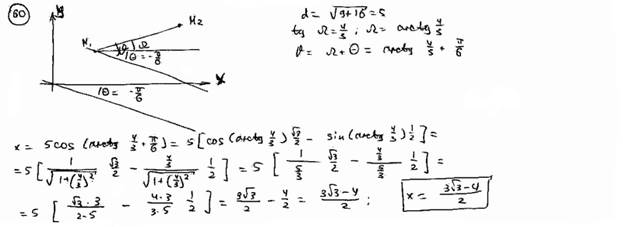
| |||||
| 61 |
Даны две точки P(-5; 2), Q(3; 1).
Найти проекцию отрезка  на ось, которая составляет с осью Ox угол на ось, которая составляет с осью Ox угол 

| |||||
| 62 |
Даны две точки M1(2; -2), M2(7; -3).
Найти проекцию отрезка  на ось, проходящую через точки
A(5; -4), B(-7; 1) и направленную: на ось, проходящую через точки
A(5; -4), B(-7; 1) и направленную:
| |||||
| 62.1 | от А к В; | |||||
| 62.2 | от В к А.

| |||||
| 63 | Даны точки A(0; 0), B(3; -4), C(-3; 4), D(-2; 2), E(10; -3). Определить расстояние d между точками: | |||||
| 63.1 | А и В. | |||||
| 63.2 | В и С. | |||||
| 63.3 | А и С. | |||||
| 63.4 | C и D. | |||||
| 63.5 | A и D. | |||||
| 63.6 | D и E.

| |||||
| 64 | Даны две смежные вершины квадрата A(3; -7) и В(-1; 4).
Вычислить его площадь.

| |||||
| 65 | Даны две противоположные вершины квадрата P(3; 5), Q(1; -3).
Вычислить его площадь.

| |||||
| 66 | Вычислить площадь правильного треугольника, две вершины которого суть
A(-3; 2), B(1; 6).

| |||||
| 67 | Даны три вершины А(3; -7), В(5; -7), С(-2; 5) параллелограмма ABCD,
четвертая вершина которого D противоположна B.
Определить длины диагоналей того параллелограмма.

| |||||
| 68 | Сторона ромба равна  , две его противоположные вершины суть точки
P(4; 9), Q(-2; 1). Вычислить площадь этого ромба. , две его противоположные вершины суть точки
P(4; 9), Q(-2; 1). Вычислить площадь этого ромба.

| |||||
| 69 | Сторона ромба равна  , две его противоположные вершины суть точки
P(3; -4), Q(1; 2). Вычислить длину высоты этого ромба. , две его противоположные вершины суть точки
P(3; -4), Q(1; 2). Вычислить длину высоты этого ромба.

| |||||
| 70 | Доказать, что точки А(3; -5), В(-2; -7), С(18; 1) лежат на одной прямой.

| |||||
| 71 | Доказать, что треугольник с вершинами A1(1; 1), A2(2; 3), A3(5; -1) прямоугольный.

| |||||
| 72 | Доказать, что точки А(2; 2), В(-1; 6), С(-5; 3), D(-2; -1) являются вершинами квадрата.

| |||||
| 73 | Определить, есть ли среди внутренних углов треугольника с вершинами
M1(1; 1), M2(0; 2), M3(2; -1) тупой угол.

| |||||
| 74 | Доказать, что все внутренние углы треугольника с вершинами
M(-1; 3), N(1; 2), P(0, 4) острые.

| |||||
| 75 | Вершины треугольника суть точки A(5; 0), B(0; 1), C(3; 3).
Вычислить его внутренние углы.

| |||||
| 76 | Вершины треугольника суть точки А( ; 1), B(0, 2), C( ; 1), B(0, 2), C( ; 2).
Вычислить его внешний угол при вершине А. ; 2).
Вычислить его внешний угол при вершине А.

| |||||
| 77 | На оси абсцисс найти такую точку М,
расстояние от которой до точки N(2; -3) равнялось бы 5.

| |||||
| 78 | На оси ординат найти такую точку М, расстояние от которой до точки
N(-8; 13 равнялось бы 17.

| |||||
| 79 | Даны две точки M(2; 2), N(5; -2); на оси абсцисс найти такую точку
Р, чтобы угол MPN был прямым.

| |||||
| 80 | Через точку А(4; 2) проведена окружность, касающаяся обеих координатных осей.
Определить ее центр С и радиус R.

| |||||
| 81 | Через точку М1(1; -2) проведена окружность радиуса 5, касающаяся оси Ox.
Определить центр С окружности.

| |||||
| 82 | Определить координаты точки М2, симметричной точке М1(1; 2)
относительно прямой, проходящей через точки А(1; 0), В(-1; -2).

| |||||
| 83 | Даны две противоположные вершины квадрата А(3; 0) и С(-4; 1).
Найти две его другие вершины.

| |||||
| 84 | Даны две смежные веришны квадрата А(2; -1) и В(-1; 3).
Определить две его другие вершины.

| |||||
| 85 | Даны вершины треугольника M1(-3; 6), M2(9; -10), M3(-5; 4).
Определить центр С и радиус R круга, описанного около этого треугольника.

| |||||

Поиск:
Рекомендуем:
 Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ
Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки)
Нейроглия (или проще глия, глиальные клетки)
Категории:
Глава 4. Направленный отрезок. Проекция отрезка на произвольную ось. Проекции отрезка на координатные оси. Длина и полярный угол отрезка. Расстояние между двумя точками
|
|
|
|
|
|
|
|
|
|
Дата добавления: 2016-10-22; Мы поможем в написании ваших работ!; просмотров: 1478 | Нарушение авторских прав
Поиск на сайте:
Лучшие изречения:

