Пусть данная фигура, ограниченная линиями y=f1(x), y=f2(x), x=a, x=b, представляет собой материальную плоскую фигуру. Поверхностною плотность, то есть массу единицы площади поверхности, будем считать постоянной и равной d для всех частей фигуры.
Разобьем данную фигуру прямыми x=a, x=x1,..., x=xn=b на полоски ширины Dx1, Dx2,..., Dxn. Масса каждой полоски будет равна произведению ее площади на плотность d. Если каждую полоску заменить прямоугольником (рис.1) с основанием Dxi и высотой f2(x)-f1(x), где x, то масса полоски будет приближенно равна

(i = 1, 2,.,n).
Приближенно центр тяжести этой полоски будет находиться в центре соответствующего прямоугольника:

Заменяя теперь каждую полоску материальной точкой, масса которой равна массе соответствующей полоски и сосредоточена в центре тяжести этой полоски, найдем приближенное значение центра тяжести всей фигуры:

Переходя к пределу при  , получим точные координаты центра тяжести данной фигуры:
, получим точные координаты центра тяжести данной фигуры:

Эти формулы справедливы для любой однородной (т.е. имеющей постоянную плотность во всех точках) плоской фигуры. Как видно, координаты центра тяжести не зависят от плотности d фигуры (в процессе вычисления d сократилось).
Св-ва неопр-ного интеграла
1) 
|
| По опред. 1 имеем: |
(
|
| f(x) 0 |
2) d( ,имеем ,имеем
|
d(
|
| f(x) |
3)  ,в справедливости этого св-ва можно убедиться,найдя диф-л от левой и правой частей: ,в справедливости этого св-ва можно убедиться,найдя диф-л от левой и правой частей:
|
d( ,согласно св-ву 2, ,согласно св-ву 2,
|

|
4)  , ,
|
| находим произв-ю от левой части: |
(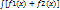 dx)`=f1(x) dx)`=f1(x)  f2(x), согласно св-ву 1. f2(x), согласно св-ву 1.
|
| Находим произв=ю от правой части: |
( , производные левой и правой частей совпадают,след-но это рав-во верно , производные левой и правой частей совпадают,след-но это рав-во верно
|
5)  где а-постоянная,т.е.пост-ю можно выносить за знак интеграла. где а-постоянная,т.е.пост-ю можно выносить за знак интеграла.
|
| Произв-я от левой части:(1 св-во) |

|
| Произв-я от правой части: |
(a 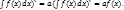 Произв-е от левой и правой частей совпадают,след-но равны интегралы,стоящие слева и справа. Произв-е от левой и правой частей совпадают,след-но равны интегралы,стоящие слева и справа.
|
Двойной интеграл в полярных коор-тах
| Часный случай |

|
I=  =p =p
|
| P=I |
 pdpd pdpd 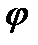
|
Выражение pdpd  являеться-элементом площади. являеться-элементом площади.
|
Таблица интегралов
1) 
|
2)  = = 
|
3) 
|
4) 
|
5) 
|
6) 
|
7) 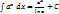
|
8) 
|
9) 
|
10) 
|
11) 
|
12) 
|
13) 
|
14) 
|
15) 
|
16) 
|
17) 
|
18) 
|
Замена перем-ных в двойном интеграле
Рассмотрим 
|
| x=(u,v), y=(u,v)-однозначные переменные ф-ии имеющие непрерывные производные |
Пусть также эта замена переменных переносит область  плоскости Xoy в некатор область плоскости Xoy в некатор область  плоскости UoV. плоскости UoV.
|
| Тогда справедлива след формула замена переменных интегрирован в двойном интеграле. |
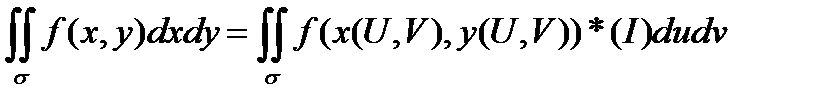
|
Где I-  - определитель Якоби или якобеан перехода от x,y к u,v - определитель Якоби или якобеан перехода от x,y к u,v
|
Интегрирование методом замены прем-х
Дано  ,сделаем замену. ,сделаем замену. 
|
x= 
|
| Подставляем это вертикально в данный интеграл. Имеем: |

|
Докажем. Для этого найдём произв-ю от левой части: (
|
От правой части: ( , ,
|
f( ,т.е.произв-е левой и правой частей совпадают,зн-т и интегралы справа и слева совпадают. ,т.е.произв-е левой и правой частей совпадают,зн-т и интегралы справа и слева совпадают.
|
 сделаем замену переменных сделаем замену переменных
|
x=  , dx=( , dx=( dt, t=lnx dt, t=lnx
|
 , ,  введем замену t=lnx, dt= введем замену t=lnx, dt= 
|
= 
|






