Теорема: если числовой ряд а1+ а2+…+аn+… (1) сходится, то предел его общ. члена при неогранич. Возрастании номера n-0
Limn→∞ an =0
Док-во: если ряд 1 сходится, то сущ-т предел Limn→∞ Sn(6), что тогда сущ-т также и предел Lim Sn-1=S(7) (т.к. если n→∞,то и n→1 тоже =>8
Вытикая из (6) и (7) имеем:
Limn→∞ Sn - Limn→0 = 0
Limn→∞ (Sn – Sn-1) = 0 ((Sn –Sn-1)=0)=an
(Sn= SN-1 + an)
Limn→∞ an = 0
Знаем, что это признак явл-ся необходимым, но сущ. недостаток, если Limn→∞ an =0 то это не означает, что ряд 1 сходится
Частные производные
Опр.Частной производной от ф-ции z=f(x,y) по переменной х, наз.предел отношения частного приращения 
этой ф-ции к приращению 
. Обозначим 
или 
. 
; 
. Определяем частную производную от переменной у: 
; 
Частной производной ф-ции z=f(x,y) по переменной х наз.обычная производная от ф-ции одной переменной х в кот.приращена ф-ция f(x,y), если предположить, что 2-ая переменная у постоянная. Производная этой ф-ции по у находится в предположении, что х постоянная.
Теоремы о сх-сти рядов
Теорема1: Если сходится ряд, получившийся из данного ряда отбрасыванием нескольких его членов, то сходится и сам данный ряд. Обратно, если сходится данный ряд, то сходится и ряд, получившийся из данного отбрасыванием нескольких членов.
Теорема2: Если ряд 
сходится и его сумма равна S, то ряд 
, где с – какое-либо фиксированное число, также сходится и его сумма равна сS.
Теорема3: Если ряды 
и 
сходятся и их суммы соответственно равны Sa и Sb, то ряды 
и 
тоже сходятся и их суммы соответственно равны Sa+Sb и Sa-Sb.
Полный диф-ал
Пусть дана ф-ция z-х перем-ых z=f(x,y).Ее полное приращ-е по опр-ю Δz= f(x+Δx,y)- f(x,y).Можно показ.,что это приращ-е можно предст. в виде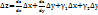 
, где 
(1) 
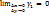
Гл.часть полн.приращ-я Δz, линейная относ-но Δx, Δу,полным дифф-лом ф-ии z(x,y).Обозн. dz.
.Диф-лы независ.перем-ых х и у по опред-ю равны их приращ-ям dx=Δx, dy=Δy. Поэтому 
.При достаточно малых зн-ях Δx,Δy 2-мя послед.слагаемыми в ф-ле(1). Можно принебречь.Тогда 
.
Числовые ряды.Сх-сть.Сумма ряда
Пусть дана числовая последовательность а1, а2, а3, +.., аn+
Выражение вида а1 + а2 + а3 +++ аn (1) - наз-ся числовым рядом
Числа а1, а2, +, аn - наз-ся членами ряда.
Числовой ряд (1) считается заданным, если извесен общий член ряда как функция an=f (n)
Произ-ная сложной ф-ции 2 перем-х.
Пусть дана ф-ия z= z (u,v),где перем-ые u и v не явл. независ., а тоже явл.ф-ми от 2-х перем-ых х и у: U= U(x,y) V=V(x,y).Т.е. мы имеем сложн. ф-цию: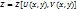 
.Найдем произв-ую этой ф-ии по перем-ной х.Дадим перем-ой х приращ-е Δх.Тогда перем-ные U и V получ. приращ-е 
, 
.При этом получ. приращ-е полное,опр-мое формулой 
: 
. Разделим обе части фор-лы наΔx.Перейдем к пределу при х→0. 
+ 
Если счит.,что ф-ии U(x,y) и V(x,y) равны, то при Δх→0, ΔU→0 и ΔV→0. Поэтому 
, 
(2).Аналогично можно найти: 
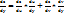.(3)
