Параметрич. задание ф-ции. Произ-ная ф-ции
Пусть xty ==ϕφ(),()- две функции одной независимой переменной. Если tT∈x=ϕ() монотонна на Т, то существует обратная к ней функция. Поэтому функцию t=−ϕ1() yt=φ(), можно рассматривать как сложную функцию, переводящую элемент х в элемент y посредством промежуточной переменной: t=−ϕ1() t
()xttxyttTytFx=⇒==⎧⎨⎩∈⇔==−ϕϕφφϕ()()(),()1 Переменную называют t параметром. В этом случае говорят, что сложная функция задана параметрически.
Замечание: всякую функцию можно задать параметрически.
Рассмотрим произвольную внутреннюю точку x0 области определения функции y = f(x).
Разность  , где x - также внутренняя точка области определения, называется приращением аргумента в точке x0. Разность  называется приращением функции в точке x0, соответствующим приращению и обозначается 
Производной функции y = f(x) в точке x0 называется предел отношения приращения функции к приращению аргумента в этой точке при стремлении приращения аргумента к нулю, если такой предел существует и конечен, т.е.
|
Нормал. закон распределения
Непрерывная случ. величина распред. по нормальному з-ну, если плотность распределения 
или 
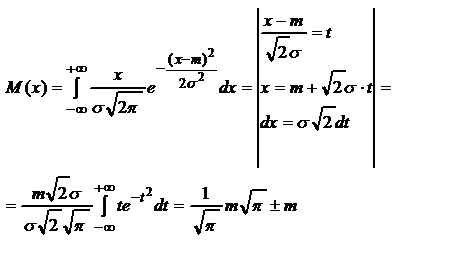
Произ-ная неявной ф-ции
Пусть значения двух переменных x и y связаны между собой некоторым уравнением, которое символически запишем так:F(x, y) = 0. (1)
Если на некотором множестве D каждому значению переменной x соответствует единственное значение y, которое вместе с x удовлетворяет уравнению (1), то будем говорить, что это уравнение задает неявную функцию y=f(x).
Из определения следует, что для любой неявной функции y=f(x), заданной уравнением (1), имеет место тождество F(x, f(x)) ≡ 0, справедливое при всех x Î D.
Заметим, что каждая явная функция y=f(x) может быть представлена и как неявная y–f(x) = 0.
Таким образом, неявная функция – это определенный способ задания зависимости между переменными x и y.
Чтобы найти производную у' неявной функции F(x, y)=0, нужно обе части этого уравнения продифференцировать по x, рассматривая у как функцию от x, и из этого полученного уравнения найти искомую производную y'. Чтобы найти y'', нужно уравнение F(x, y)=0 дважды продифференцировать по x и выразить y'' и т.д.
2.2.ф-ция распр-ния непрер.случ.величины и её матем.хар-ка
Ф-ция распределения СВ.
Ф-цией распределения или интегральной ф-цией наз. F(X)=P(X<x). Вер.того вер.Х меньше чем х:
| xi | X1 | X2 | … | xn |
| pi | P1 | P2 | … | pn |
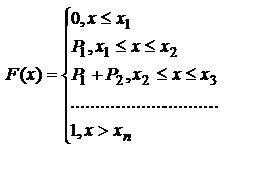
Свойства:
1. 
2.F(X)-функция неубывающая
X1 X2 X
Рассмотрим событие 
;
; 
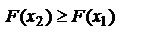-большему значению аргумента соответствует большее значение функции.
3. 
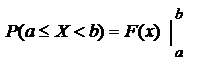
Замечание: если случ. Величина X непрерывна то вероятность того что СВХ примет значение х равна 0.
ж
Диф-ал
Дифференциа́л— линейная часть приращения функции. Итак, график дифференцируемой функции в окрестности каждой своей точки сколь угодно близко приближается к графику касательной в силу равенства: где α – бесконечно малая в окрестности функция. Для приближенного вычисления значения функции f в точке x0 + Δx эту бесконечно малую функцию можно отбросить: 
Линейную функцию 
называют дифференциалом функции f в точке и обозначают df. Для функции x производная в каждой точке равна 1, то есть. Поэтому пишут: 
Приближенное значение функции вблизи точки равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом: 
. Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется функция.
Дифференциал функции
Геометрически дифференциал функции df – это приращение ординаты касательной к графику функции в данной точке при изменении абсциссы точки на dx.
вер-сть попадания в заданный интервал непрер.случ.вел-ны
Вероятность того, что значение случайной величины Fx (x) попадает в интервал (a, b), равная P(a < x < b) = Fx (b) -Fx (a), вычисляется по формулам:
- для непрерывной случайной величины и
- для дискретной случайной величины.
Если a= - 
, то 
если b= , то 
4.1.применение диф-ла в приближённых вычис-ях
Пусть нам известно значение функции y0=f(x0) и ее производной y0' = f '(x0) в точке x0. Покажем, как найти значение функции в некоторой близкой точке x.
Как мы уже выяснили приращение функции Δyможно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dyили Δy»f'(x0)·Δx.
Т.к., по определению, Δy = f(x) – f(x0), то f(x) – f(x0)≈f'(x0)·Δx.
Откуда f(x) ≈ f(x0) + f'(x0)·Δx
y = x2 – 2x. Найти приближенно, с помощью дифференциала, изменение y (т.е. Δy), когда x изменяется от 3 до 3,01.
Имеем Δy≈dy=f'(x)·Δx.
f'(x)=2x – 2,f'(3)=4, Δx=0,01.
Поэтому Δy ≈ 4·0,01 = 0,04. y = x2 – 2x.
Пример:Найти приближенно, с помощью дифференциала, изменение y (т.е. Δy), когда x изменяется от 3 до 3,01.
Имеем Δy≈dy=f'(x)·Δx.
f'(x)=2x – 2,f'(3)=4, Δx=0,01.
Поэтому Δy ≈ 4·0,01 = 0,04.
