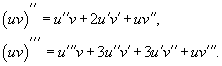
33.Дискретная случ.вел-на.Закон её распр-ния
| Перемен.величина x,кот принимается в результате испытаний между конечной и бесконечной последовательности значений x1,x2,…,хn,…наз. дискретной случайной величиной.отношение, устанавливающее связь между отдельными возможными значениями случайной величины и соответств. им вероятностями, наз. законом распред. дискретн. случайной величины. | ||||||||||
| Дискрет.случайная величина мот быть задана различн.способами | ||||||||||
| 1)табличн | ||||||||||
2)графический | ||||||||||
| ||||||||||
| 3)аналитический | ||||||||||
| Pk=(xk) | ||||||||||
Т.к случайная величина принимает одно из своих возм значений, то  .
| ||||||||||
| Значение величины имеющая наиб вероятность называется модой |
Диф-лы высших порядков
Рассм. дифференциал функции y=f(x) в произвольной точке промеж. (a,b):dy = f’(x)dx. Здесь dx - приращ. независимой переменной, кот. явл. числом и не зависит от x. Сам же дифференциал есть функция от x, и можно вычисл, дифференциал от этой функции: 
При 
этот дифференциал от дифференциала называется дифференциалом 2-ого порядка и вычисл. по формуле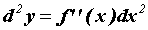 
Аналогично вычисл. дифференциал любого порядка 
.
Формула Байеса.Вер-сть гипотез
| Пусть событие А может происходить только с одним из событий В1,В2,…Вn,образуемых полную группу событий В1,В2,…Вn будем наз гипотезами.Вероятность события А может быть построена по формуле полной вероятности |
| P(A)=P(B1)*P(A/B1)+ P(B2)*P(A/B2)+ P(Bn)*P(A/Bn)(1) |
| A-нужно найти вероятность того,что оно произошло вместе с гипотезой P(Bk/A) |
| Вероятность событий A и Вк по правилу сложения вероятностей может быть представлено 2-мя способами: |
| P(AnBk)= P(Bk)*P(A/Bk) |
| P(AnBk)= P(A)*P(Bk/A) |
| Прировняли две части.После этого получили |
| P(Bk/A)= P(Bk)*P(A/Bk)/ P(A) |
| Знаменатель может быть найден по формуле полн вероятности(1) |
| Тогда формула Байесa принимает вид |
P(Bk/A)= P(Bk)*P(A/Bk)/ 
|
Теорема Роля
Если вещественная функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
Если непрерывная функция обращается в ноль в n различных точках, то ее производная обращается в ноль по крайней мере в n − 1 различных точках[1], причем эти нули производной лежат в выпуклой оболочке нулей исходной функции. Это следствие легко проверяется для случая действительных корней, однако имеет место и в комплексном случае.
Формула полной вер-сти
| Пусть имеется группа событий B 1, B 2,..., Bn, обладающая следующими свойствами: |
| 1) все события попарно несовместны |
| 2) их объединение образует пространство элементарных исходов |
| В этом случае будем говорить, что B 1, B 2,..., Bn образуют полную группу событий. Такие события иногда называют гипотезами. |
| формула полной вероятности: |
| P(A)=P(B1)*P(A/B1)+ P(B2)*P(A/B2)+ P(Bn)*P(A/Bn) |
Теорема Лагранжа
Если функция f(x) непрерывна на замкнутом интервале [а, b] и внутри него имеет производную f ' (x), то найдется хотя бы одно такое значение x0 (a < x0 < b), что
f(b) - f(a) = (b - a)f '(x).
Доказательство. Рассмотрим вспомогательную функцию
F(x) = f(x) - k(x - a),
где - угловой коэффициент хорды AB (смотри рисунок 2).
Эта функция удовлетворяет всем условиям теоремы Ролля.
В самом деле, при x = a имеем F(a) = f(a) - k(a - a) = f(a), при x = b имеем
Кроме того, так как функция f(x) и k(x - a) непрерывны на [a, b] и диференцируемы в (a, b), то и функция F(x) = f(x) - k(x - a) непрерывна на [a, b] и диференцируема в (a, b).
