Комплексным числом называется выражение вида z=x+iy, где x,y – действительные числа, i – мнимая единица, i2 = -1,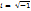 
|
| Числа z=x+iy и z=x-iy отличающиеся только знаком мнимой части называются сопряженными. |
| Комплексное число z=x+iy считается равным нулю z=0, тогда, когда его действительная и мнимая части равны нулю x = 0, y = 0. |
| Два комплексных числа z1=x1+iy1, z2=x2+iy2 считаются равными тогда, когда равны их действительные и мнимые части: x1 = x2, y1 = y2. |
Замена перем-х в тройном интеграле
Пусть исходный тройной интеграл задан в декартовых координатах x, y, z в области U: 
Требуется вычислить данный интеграл в новых координатах u, v, w. Взаимосвязь старых и новых координат описывается соотношениями:
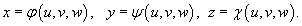
Предполагается, что выполнены следующие условия:
Функции φ, ψ, χ непрерывны вместе со своими частными производными;
Существует взаимно-однозначное соответствие между точками области интегрирования U в пространстве xyz и точками области U' в пространстве uvw;
Якобиан преобразования I (u,v,w), равный
отличен от нуля и сохраняет постоянный знак всюду в области интегрирования U.
Тогда формула замены переменных в тройном интеграле записывается в виде: 
В приведенном выражении означает абсолютное значение якобиана.
Тригонометрич.форма записи комплексного числа.
| Тригонометрическая форма записи комплексного числа: |
|
Вычисление тройного интеграла в декартовых коор-тах
| Рассмотрим трёхмерную область V обладающую. Свойствами. |
| 1) любая прямая проходящая через точку принадлежащую этой области пораллельно оси оси Oz пересекает границу этой области не более чем в 2-х точках. |
2) Проекцию  этой области на плоскость xOy явл. Правильной двумерной областью.
|
| Тогда справедливы след. Формула для вычисления тройного интеграла декартовых координат. |
|
Осн.действия над компл.числами в алгебраич.форме
| Алгебраическая форма комплексного числа: z=x + iy |
| Рассмотрим два комплексных числа z1=x1+iy1 и z2=x2+iy2 |
| Правила: |
| 1) Сумма: z1+z2= (x1+x2)+i(y1+y2) |
| 2) Разность: z1-z2= (x1-x2)+i(y1-y2) |
| 3)Правило умножения комплексных чисел: z1*z2= (x1x2-y1y2)+i(x1y2+x2y1) |
4) Частное: 
|
| Заметим, что если мнимые части y1, y2 комплексных чисел равны нулю, то из правила 1, 2, 3, 4 получаются обычные правила действие с действительными числами |
Св-ва тройного интеграла
| 1)множитель нужно выносить за знак интеграла |
 
|
| K-const |
| 2)интеграл от суммы функции равен сумме интегралов |
|
3)Если в области v выполняются неравенства  то тройной интеграл
|
|
| 4)Если область v состоит из нескольких областей V1,V2,V3……Vk,то тройной интеграл области V равен: |
|
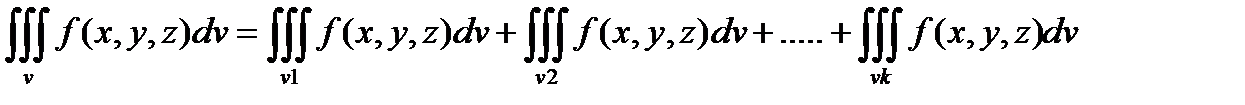
| 5)Теорема о среднем значении. |
Если функция f(x,y,z) непрерывна f ограниченной замкнутой трехмерной области V, то в этой области находиться точка (Xo,Yo,Zo) такая что тройной интеграл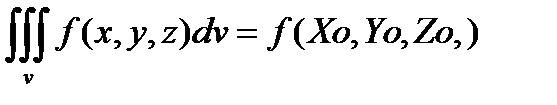 
|
| Здесь значение f(Xo,Yo,Zo) называется среднее занчение фун-ий f(x,y,z) в области V. |
