| Теорема: 1. Если функция f(x) имеющая производную на отрезке [а;b] возрастает (убывает) на этом отрезке, то f’(x) >= 0 (f(x) <=0)
|
| 2. Если функция f(x) не прерывна на отрезке [a,b] и диф-ма на интервале (a,b) и если f’(x)>0 (f’(x)<0), то ф-ия f(x) возрастает (убывает) на отрезке [a;b].
|
| Доказательство:
|
| 1.Пусть ф-ия f(x) возрастает на отрезке [a;b]. Дадим перемен х приращение ∆х. Тогда ф-ия f(x) получит приращение ∆y = f(x+∆x)-f(x). Рассмотрим отношение:
|
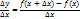
|
| Если ∆x>0, то ∆y>0 – ф-ия возрастает.
|
| Если ∆х<0, то ∆y<0- ф-ия убывает.
|
В любом случае 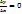
|
| И тогда в последнем неравенстве, переходя к пределу при ∆х→0 имеем:
|
 , т. е. f’(x)>=0 и т. д. , т. е. f’(x)>=0 и т. д.
|
| Аналогично можно показать, что если f(x) убывает, то f’(x)<=0.
|
| 2. Пусть f’(x)>0. Поскольку ф-ия f(x) дифференцируема, то к ней применима теорема Лоранжа.
|
| f(x2) –f(x1) = f’(ξ) (x2-x1) ξ – кси
|
| Поэтому, если f’(ξ)>0, то при x2 > x1 – f(x2 –x1), а при x2 < x1 – f(x2) < f(x1), т.е. f(x) возрастает.
|
| Аналогично можно показать, что если f’(x) < 0, то f(x) убывает.
|
| Доказанная теорема имеет простой геометрический смысл:
|

|
| Для возрастающей функции касательная к его графику образует острый угол α с положительным направлением оси Ох. Тогда f’(x) = tg α >0. Либо в некоторых точках касательная параллельна оси Ох α=0 f’(x) = tg 0 = 0 f’(x)>0.
|

|
| Если ф-ия f(x) убывает, то касательная к ее графику образует тупой угол с положительным направлением оси Ох, либо к некот точкам оси Ох, тогда α=0.
|
| В обоих случаях f’(x)= tg α = 0.
|
28.классич.опр-ние вер-стей.Непосред.подсчёт вер-стей
| Иногда вероятность события можно оценить не проводя испытаний, исходя из условий проведения испытаний.
|
| Пример:рассм. Игральную кость. Пусть наилуч. событие выпадение граней с числами L. Выпадение люб. грани
|
| одинаково возможно,в силу симметрии этой кости. Такие события, как выпадение различ. костей наз. равновозможными. При большом числе бросаний выпадение любого числа L (L=5) будет происходить приблиз. В 1/6 от числа всех испытаний. Относ. частота p=1/6, поэт. Вероятность появл. грани можно считать = 1/6.
|
| Случайные события наз. несовмест. в дан. испыт.,если никакие из 2 из них не могут появится вместе в одном из испытаний. Будем говорить, что случ. события образ. полную группу может появится люб. событие из данной группы и не может появится никакое другое событие несовместное с ними в данных испытаниях.События,кот образуют полную группу равновозможных не совместных событий наз случаями или шансами. Выпадение грани образ. полную группу из 6 равновоз-ых несовмест. событий.События из этой группы наз. благоприятствующими появлению некот. события А, если появление этого события влечет за собой появление события А.ПРИМЕР:
|
| Рассм. урну. в кот мах 10 шаров.Пустиь все шары пронумер. От 1 до 10.Пусть 1,2,3,4-белые,остальные-черные.Мы наугад достаем 1 из шаров.тогда пустьнаше событие А-появл. белого,тогда появление шара с №1,так же кА и шаров с №2,3,4 явл событиями благоприятствующ. Появлению белого шара. Вероятностью р события А наз. отношение m числа случаев благоприятствующих появл. события А к числу n всех случаев.образующих полную группу равновозможных не совмест. событий.
|
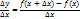
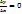
 , т. е. f’(x)>=0 и т. д.
, т. е. f’(x)>=0 и т. д.








