Этот метод предназначен для решения СЛАУ 
(1) с веществ., сим-ой, положительно определенной м-цей. Обозн. решение сист. (1) через 
. Из положит. опред. и сим-ти матрицы следует 
. Отсюда видно, что минимум функц-ла 
достигается на решении 
сист. (1). Т. о., решение сист. (1) сводится к минимизации функц-ла. Для минимизации функц-ла воспользуемся градиентным методом. В направлении градиента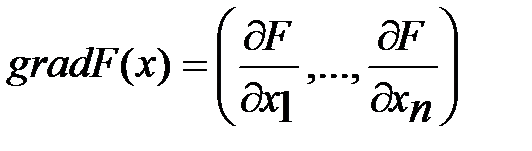 
скорость возрастания функц-ла наибольшая. В данном случае для градиента функц-ла справедливо рав-во 
. Действительно, проводя диф-ие, имеем
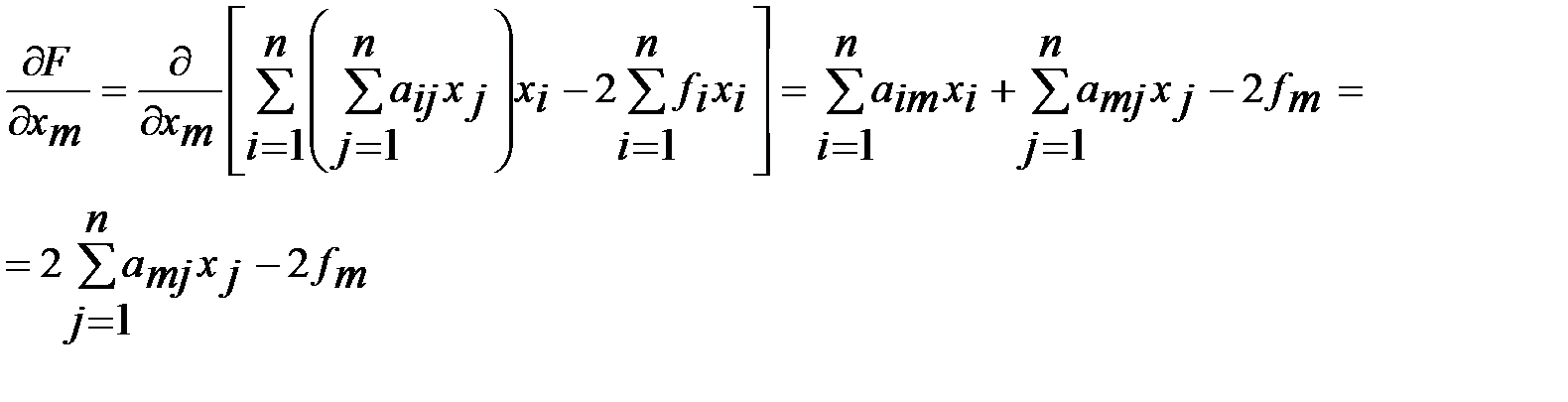Вектор 
задает направление, противоп. градиенту, то есть направление, в кот. скорость убывания функц-ла наибольшая, если двигаться из точки 
. Пусть найдено приближение 
к решению. Рассм. процесс нахождения очередного приближ. 
в методе скорейшего спуска. Направление наибольшей скорости убывания функционала в точке 
задается вектором 
.(2) Этот вектор наз. еще вектором невязок сист. для приближения 
. Точка 
находится на поверхности уровня 
и вектор невязок 
ортогонален этой поверхности уровня в точке 
. Будем искать минимум функц-ла на множ. точек 
, где числовой параметр t³0. При этом для функц-ла имеем 
, т.е. задача минимизации функц-ла на направлении наибольшей скорости его убывания сводится к нахождению минимума ф. одного переменного. Соотв. знач. числового параметра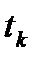 
определ. из усл. равенства нулю производной
.
Подставляя сюда выражение для 
, получаем ур.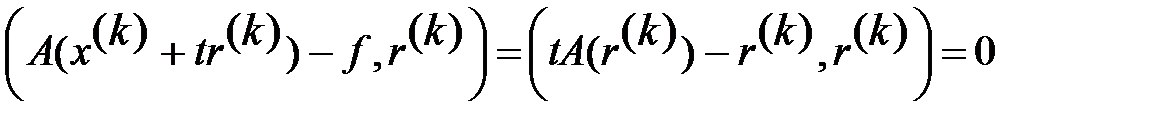 
. Отсюда 
(3)
Очередное приближение в методе скорейшего спуска выч-ся по ф-ле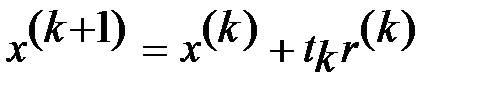 
(4). В методе скорейшего спуска нужно задать нач. приближ. 
к решению сист. (1) и по расчетным форм. (2), (3), (4) вычислять очередные приближения до получения решения с требуемой точностью.
Теорема. Если м-ца A вещественная, сим-ая и полож. определенная, то последовательные приближения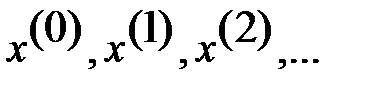 
, построенные по методу покоорд. спуска, сходятся к решению сист. 
при любом нач. приближении со скоростью геометрич. прогрессии.
Степенной метод решения частичной проблемы собств. знач.
Пусть собст. знач. матр. 
удовл. нер-ам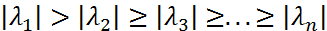 
. Будем считать также, что матрица обладает полной сист. собств. векторов. Возьмем произв-ый вектор 
, разл. его по сист. собст-х вект. 
и обр. последовательность векторов по правилу 
(1)
При этом получаем:
,…, 
.
Компоненты векторов посл-ти можно представить в виде.
(2)
Найдем выражение для отношения компонент соседних векторов в последовательности (1)
Так как 
,отсюда имеем.
(3)
В сист. методе построенная посл. (1) прекращается, когда с заданной точн. для всех 
и 
отнош. 
будет одинаковым, тогда 
, а за собств. вектор можно принять 
, где 
.