Рассм. сис-му лин. алгебр. ур. Ax=b (1), где
 . Будем предполагать, что det(A)≠0, т.е. сист. (1) однозначно разрешима при любой правой части. Перепишем (1) в развернутом виде
. Будем предполагать, что det(A)≠0, т.е. сист. (1) однозначно разрешима при любой правой части. Перепишем (1) в развернутом виде  (2). Идея метода Гаусса в приведении матрицы А в (1) к треугольному виду. После этого нахождение вектора x не будет составлять труда. На (k-1)-ом шаге метода Гаусса сист. (2) приводится к виду:
(2). Идея метода Гаусса в приведении матрицы А в (1) к треугольному виду. После этого нахождение вектора x не будет составлять труда. На (k-1)-ом шаге метода Гаусса сист. (2) приводится к виду:  , (3)
, (3)
 . (4) На k-ом шаге метода Гаусса обрабатыв. только подсист. (4). Вначале приводим 1-ый коэффициент 1-ого ур. в (4) к единице, т.е.
. (4) На k-ом шаге метода Гаусса обрабатыв. только подсист. (4). Вначале приводим 1-ый коэффициент 1-ого ур. в (4) к единице, т.е.  , коэфф. кот. вычис. через коэфф. сист. (4) по расчетной форм.
, коэфф. кот. вычис. через коэфф. сист. (4) по расчетной форм.  (5). Далее из всех ур. подсист. (4) начиная со 2-го исключает неизвестную
(5). Далее из всех ур. подсист. (4) начиная со 2-го исключает неизвестную  ,т.е. все ур. подсист. (4) начинаясо 2-го приводим к виду
,т.е. все ур. подсист. (4) начинаясо 2-го приводим к виду 
Коэфф. сист. рассчитываются по форм.  (6)
(6)
На этом заканчивается k-ый шаг метода и начин. очередной k+1 шаг. Указанные шаги повторяются до тех пор, пока исходная сист. (2) не будет приведена к виду:
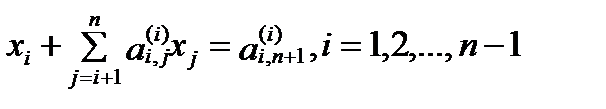 ,(7)
,(7)  (8). На этом заканчивается прямой ход метода Гаусса и начинается обратный. Из последнего ур.(8)
(8). На этом заканчивается прямой ход метода Гаусса и начинается обратный. Из последнего ур.(8)  Далее, двигаясь по сист. снизу-вверх находим
Далее, двигаясь по сист. снизу-вверх находим 
Замечание. При реализации вычислений по ф-лам (5) (6) прдполагаем 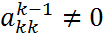 . В случае нарушения этого усл. необходимо соотв. образом переставить ур. в (4). Замечание. В ходе вычислен по (5) определитель м-цы А делится на величину
. В случае нарушения этого усл. необходимо соотв. образом переставить ур. в (4). Замечание. В ходе вычислен по (5) определитель м-цы А делится на величину 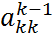 . Определит системы (7)(8) равен
. Определит системы (7)(8) равен  поэтому
поэтому  .
.
28.  - разложение квадратных матриц.
- разложение квадратных матриц.
Пусть  данная квадрат. матрица. Будем строить разложение этой матрицы в виде:
данная квадрат. матрица. Будем строить разложение этой матрицы в виде:  (1), где
(1), где  - нижняя (левая) треугольная матрица,
- нижняя (левая) треугольная матрица,  - верхняя (правая) треугольна матрица.
- верхняя (правая) треугольна матрица.
Теорема: Пусть все главные миноры матрицы  отличны от
отличны от  , тогда (1) существует.
, тогда (1) существует.
При этом, если диагональ одной из матриц 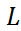 или
или  фиксированы, то такое разложение единственное.
фиксированы, то такое разложение единственное.
Вместо доказательства укажем способ построения разложения (1). Зафиксируем элементы главной диагонали матрицы  положив их равными
положив их равными  . Матричному равенству (1) поставим в соответствие равенство:
. Матричному равенству (1) поставим в соответствие равенство:
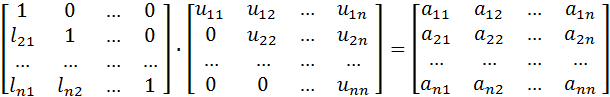 (2)
(2)
Выполнив умножение в левой части (2) получим сист. ур. относительно неизвестных  ,
,  .
.
 (3)
(3)
Специфика данной сист. позволяет решать её след. образом: из 1 строки в (3) находим  ,
,  . Из оставшейся части 1-ого столбца находим,
. Из оставшейся части 1-ого столбца находим,  ,
,  . Далее, из оставшейся части 2-ой строки находим
. Далее, из оставшейся части 2-ой строки находим  ,
, 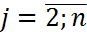 . Из оставшейся части 2-ого столбца находим
. Из оставшейся части 2-ого столбца находим  ,
, 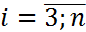 , и т.д. Последним определяем элемент
, и т.д. Последним определяем элемент 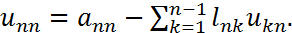
Указанный процесс решения сист. (3) можно описать посредством двух форм.:  ,
,  (4)
(4)
 ,
, 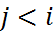 (5)
(5)
При практическом счёте необходимо вовремя переключаться с форм. (4) на форм. (5) в соотв. с указанной выше последовательностью. При выполнении усл. теоремы форм. (5):  . Действительно,
. Действительно, 
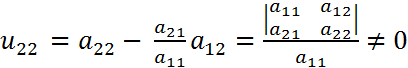 и т.д.
и т.д.
Замечание: Разложение (1) всегда осуществимо, если матрица. А явл. матрицей с диагональным преобраз., т.е. для такой матрицы выполняется 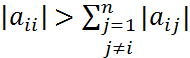 ,
, 
Рассм. сист. линейных алгебраических ур.  (6). Применим к матрице
(6). Применим к матрице 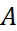
 -разложение. В итоге, будем иметь
-разложение. В итоге, будем иметь 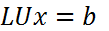 (7)
(7)
Сист. (7) представим в виде двух сист.  (8)
(8)
Поскольку матрицы  и
и 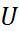 треугольные, то решения каждой из подсист. (8) идентично обратному ходу метода Гаусса.
треугольные, то решения каждой из подсист. (8) идентично обратному ходу метода Гаусса.






