Как видно из выражения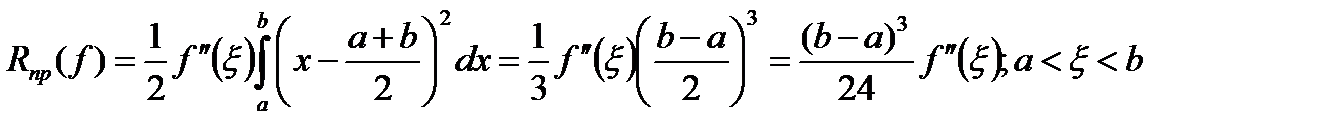 
, погрешн. квадрат. форм. средних прямоугол. есть величина третьего порядка относительно длины 
отр. интегрир. Т.о., при большой длине отр. интегрир. погрешн. указан. квадрат. форм. также может быть большой.На 
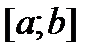введем равномерн. сетку 
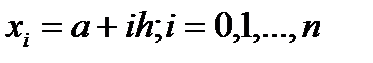с шагом 
. Интеграл по всему отр. равен сумме интегралов по частич. отр. Применяя квадрат. форм. средних прямоугол. в случае четного 
к частич. отр. 
, имеем
.
Полученную квадрат. форм. 
(1) наз. составной квадрат. форм. средних прямоугол.
Для погрешн. составной квадрат. форм. средних прямоугол. получаем
.
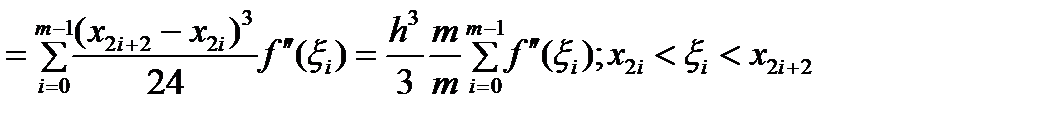Учитывая, что 
и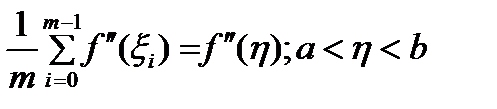 
, отсюда следует искомое равенство 
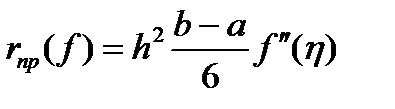. (2)
Используя квадрат. форм. трапеций при интегрир. по частич. отр.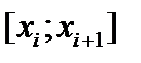 
, имеем
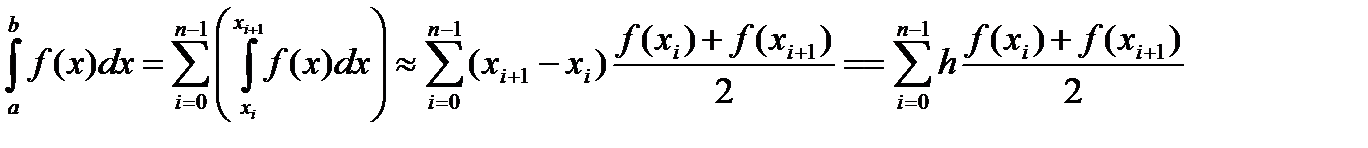Получен. квадрат. форм. 
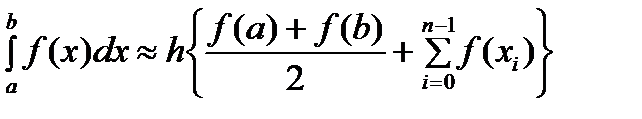(3)
наз. составной квадрат. форм. трапеций.
Для погрешн. составной квадрат. форм. трапеций получаем
.
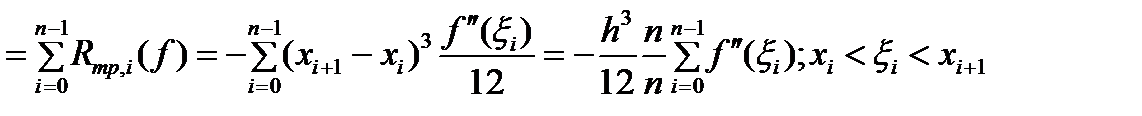Т.к.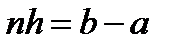 
и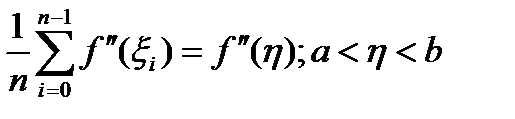 
, то искомая погрешн. представл. в виде 
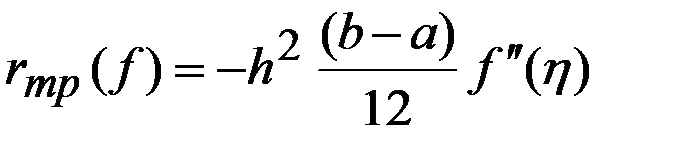. (4)
Применим теперь при четном n к интегрир. на частич. отр. квадрат. форм. парабол. Тогда
. Получ. квадр. форм. 
(5) наз. составной квадрат. форм. парабол (Симпсона).
Найдем выражение для погрешн. расчетной форм. (3).
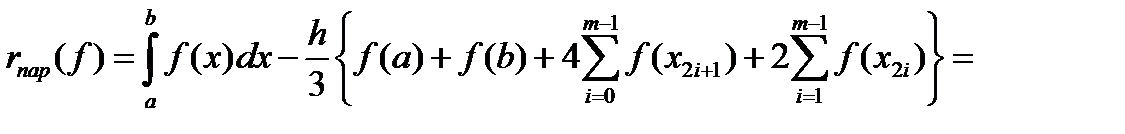
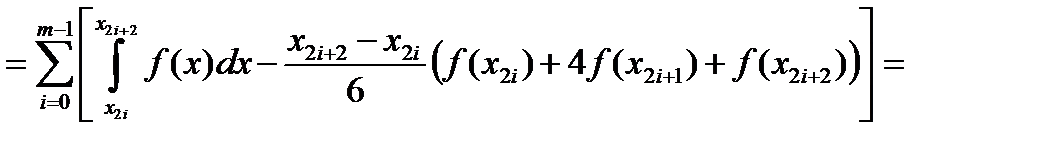
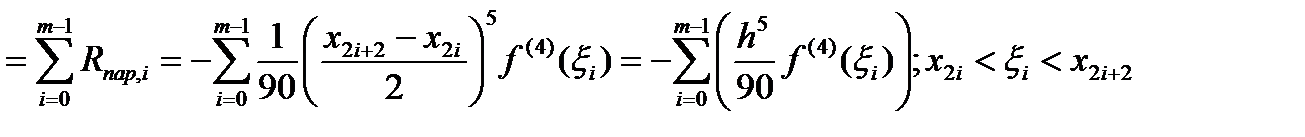Учитывая, что 
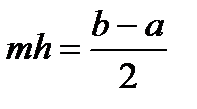и 
, отсюда следует искомое равенство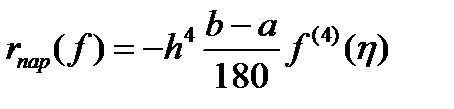 
Как видно из выражений, получ. для остаточ. членов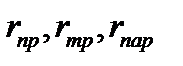 
, погрешн. составных квадрат. форм. можно сделать достаточно малой за счет выбора меньшего шага сетки h. При этом подынтеграл. ф. должна быть достаточно гладкой на .
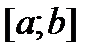Квадрат. форм. Гаусса
Опр. Говорят, что квадрат. форм.
(1)
имеет алгебраическую степень точности m, если она явл. точной для любого мног. степени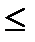 
m и существует мног. степени 
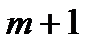, для кот. квадрат. форм. не явл. точной.
Квадрат. форм. наивысшей алгебраической степени точности наз. квадрат. форм. Гаусса (при этом n считается фиксированным). Квадрат. правило имеет алгебраическую степень точности не ниже n тогда и только тогда, когда оно явл. интерполяц. Следовательно, коэфф. квадрат. правил Гаусса определ. форм.
. (2)
Т.о., остается найти оптимал. набор узлов, при кот. интерпол. квадрат. форм. будет иметь наивысшую алгебраическую степень точности. Последняя, равна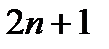 
.
Лемма. Если квадрат. правило (1) имеет алгебраическую степень точности 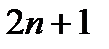, то мног. 
степени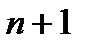 
ортогонален с весом 
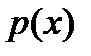на 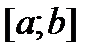любому мног. меньшей степени.
Д-во. Так как квадратурное правило (1) является точным для любого многочлена степен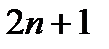и и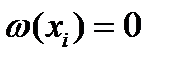 
,то при 
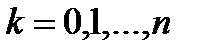имеем 
, что док-ет лемму.
Из леммы следует, что для построения квадрат. правила алгебраической степени точности 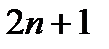необходимо найти мног. степени 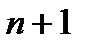, кот. был бы ортогонален любому мног. меньшей степени.
Лемма Если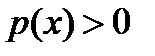 
почти всюду на 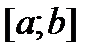, то приведенный мног. степени 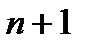, ортогональный на 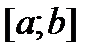с весом 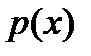любому мног. меньшей степени, существует и явл. единств. При этом все его корни простые и находятся на .
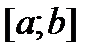Лемма Если узлами интерпол. квадрат. форм. (1) явл. нули ортогонального мног.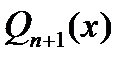 
, то квадрат. форм. точна для любого мног. степени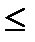 
.
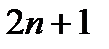Теорема. Если 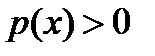почти всюду на 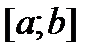, то существует квадрат. правило (1) наивысшей алгебраической степени точности .
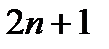Д-во. Существов. квадрат. правила (1) алгебр. степени точности 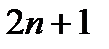непосредственно следует из лемм. Остается доказать, что нельзя построить квадрат. правило (1), точное для любого мног. степени 
. Для мног.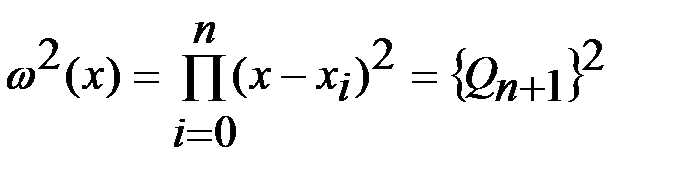 
степени имеем знач. интеграла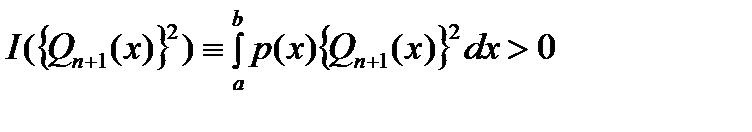 
и знач. квадрат. суммы
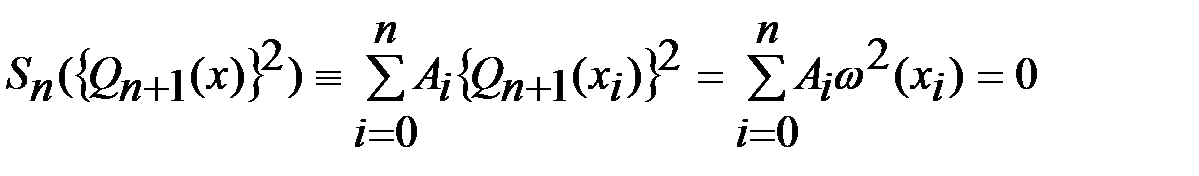
19. Квадрат. форм. Гаусса с постоянной весовой ф. Рассм. интеграл 
, (1) где 
-достат. гладкая ф. Любой конечный отр. интегрир. 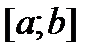линейным преобр. приводится к 
. Поскольку в данном случае весовая ф.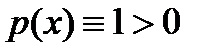 
, то квадрат. правило наивысшей алгебр. степени точности 
(2) существует. Его узлами явл. корни мн-на 
, ортогонального мн-нам меньшей степени с весом 1 на [-1;1].
Обозначим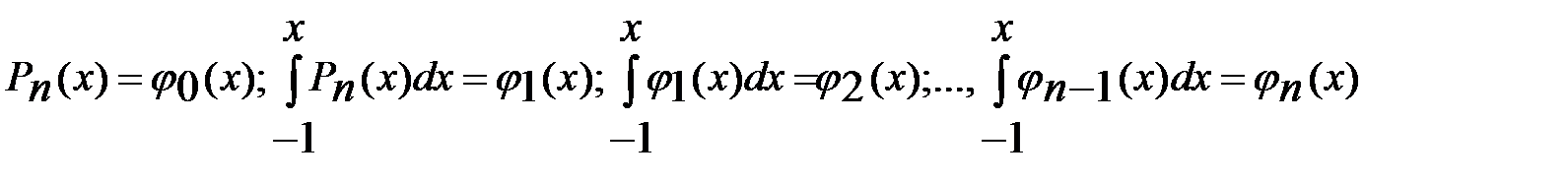 
. Очевидно, 
и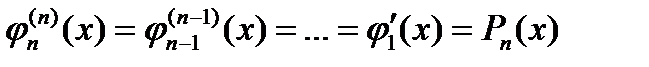 
. Возьмем произвольный мног. 
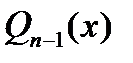степени 
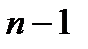. Используя услов. ортогональности и проводя интегрир. по частям, получим 
.
Продолжая процесс интегрир. по частям получим
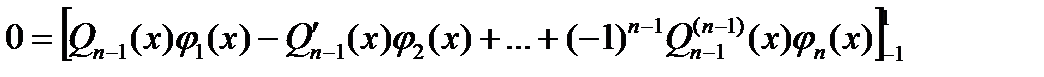Отсюда для, 
следует, что 
. Используя произвольность мног. 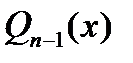, последовательно получаем далее 
.
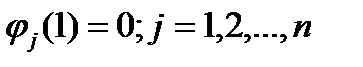Т.о., мног.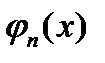 
степени 
, производные кот. определ. форм.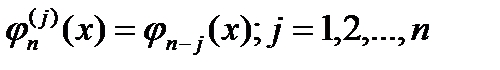 
имеет корни 
, каждый кратности n. Следовательно, этот мног. представл. в виде 
. Для искомого ортогонального мног. в результате получим выражение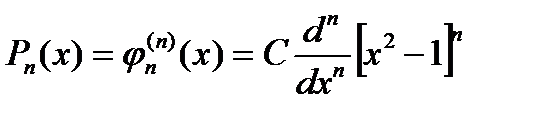 
. (3)
Ортогональные мног., определ. форм. (3) наз. мног. Лежандра. В случае выбора константы по правилу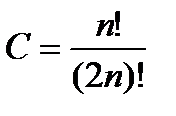 
будут получаться приведенные мног. В практике вычислений для мног. Лежандра использ. форм. Родрига 
.(4)
При этом получается квадрат нормы 
и рекуррентная форм. 
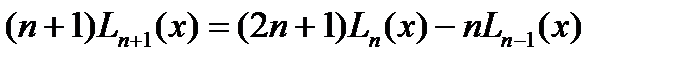.(5)
По форм.(3) находим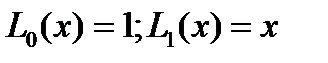 
. По форм. (4) находим 
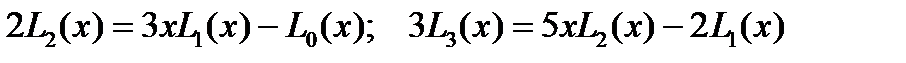. Отсюда определяем последовательно
и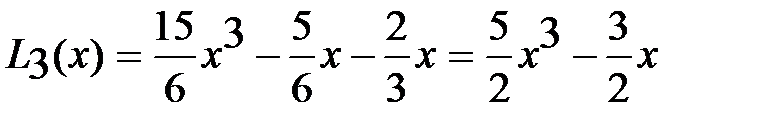 
. Построим несколько квадрат. форм. Гаусса вида (2).
При 
из ур. 
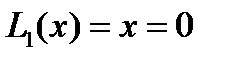получаем один корень 
, 
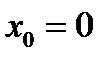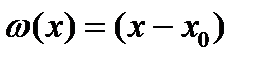и один коэфф. 
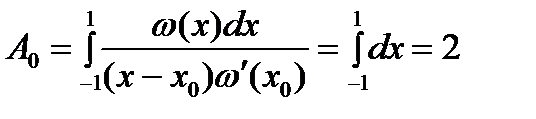. Приходим к квадрат. форм. 
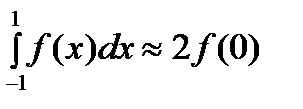, имеющей наивысшую алгебраическую степень точности 1.
При 
из ур. 
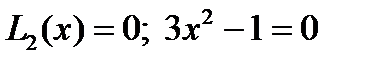получаем два корня 
, 
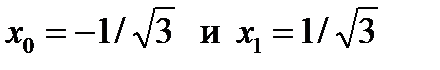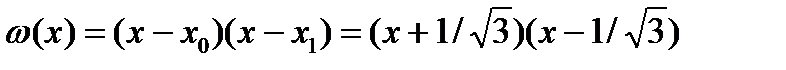и два коэфф. 
и 
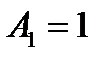. Приходим к квадрат. форм. 
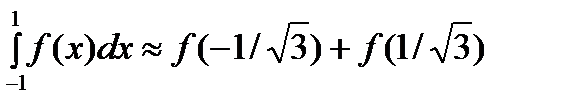, имеющей наивысшую алгебр-скую степень точности 3.
Форм. для вычисления коэфф. квадрат. форм. (2) может быть преобразована к виду 
(6)
При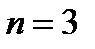 
из ур. 
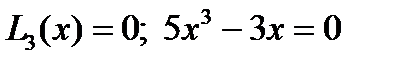получаем три корня 
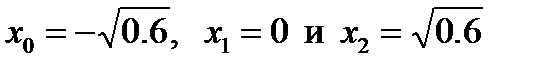и три коэфф. 
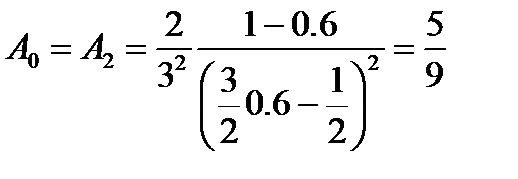и 
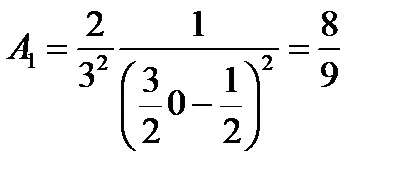. Приходим к квадрат. форм. 
, имеющей наивысшую алгебраическую степень точности 5.
