Расс. алг. ур. степени 
(1) с вещественными коэф-ми. Ур. (1) имеет ровно 
корней с учетом их кратности. Корни алг. ур. степеней 2, 3 и 4 выражаются в радикалах через свои коэфф. Корни могут быть как действительные, так и комплексные. При этом, если ур. (1) имеет корнем комплексное число 
, то корнем ур. будет и комплексно сопряженное ему число 
. Это непосредственно следует из равенства 
, справедливого для любых комплексных чисел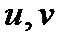 
. Т.о., алг. ур. нечетной степени имеют хотя бы один действительный корень. Для нахождения вещественных корней алг. ур. (1) можно применить методы решения численных ур. Верхнюю и нижнюю оценки модуля корней алг. ур. дает
Теор. Если 
, 
(2)
то все корни ур. (1) распол. в кольце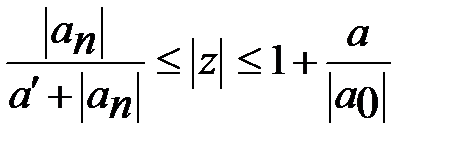 
(3)
Для оценки верхней границы положительного корня может оказаться полезной
Теорема Если 
- максимум абсолютных величин отрицательных коэфф. ур.,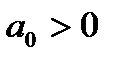 
и первый отрицательный коэфф. в ряду 
есть 
, то все положительные корни ур. меньше 
(если отрицательных коэфф. нет, то нет и положительных корней).
Для оценки верхней границы положительного корня может оказаться полезной
Теорема (теорема Ньютона). Если при 
полином 
и все его производные 
неотрицательны, то 
может быть принято за верхнюю границу положительных корней ур.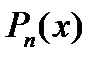 
.
Для отделения действительных корней алгебраического уравнения может быть использована
Теорема (теорема Штурма). Пусть ур. (1) не имеет кратных корней. Обозначим через 
производную 
; через 
остаток от деления 
на 
, взятый с обратнымзнаком; через 
остаток от деления 
на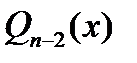 
, взятый с обратным знаком и т.д., до тех пор пока не придем к постоянной. Получим последов. ф.
, (4) наз. рядом Штурма.
Число действительных корней ур.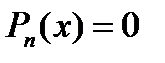 
, расположенных на 
равно разности между числом перемен знаков в последов. (4) при 
и числом перемен знаков в последов. (4) при 
.
При решении ур. (1) приходится многократно вычислять знач. мног..
Для вычисления знач.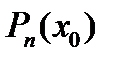 
следует пользоваться схемой Горнера, кот. можно записать в виде
(5)
Вычисления в схеме Горнера можно описать также рекуррентными соотн. 
.(6)
Схема Горнера дает также удобный способ получения частного от деления мног. 
на линейный множитель 
. Действительно, можно убедиться, выражение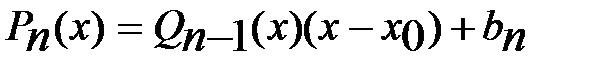 
обращается в тождество мног. 
, коэфф. кот. вычисляются по форм. (6). Нахождение частного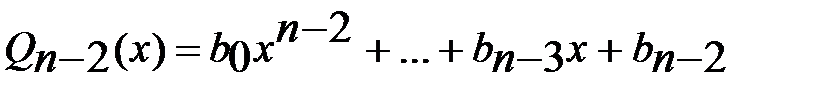 
и остатка 
от деления 
на квадратный трехчлен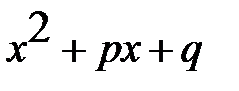 
можно провести с использованием форм.
Эти форм. получ. из тожд. 
сравнением коэфф. при одинаковых степенях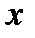 
. Покажем, что вычисление производных мног. 
в точке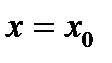 
сводится к последов. делению на линейный множитель 
. Частное от деления мног. 
на 
обозн. через 
. Тогда можно записать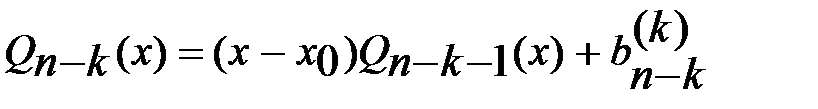 
.
При последов. делении на получаем последов. мног. 
. Коэфф. мног. вычисляются по рекуррентным форм. 
(7). Здесь для симметрии положили 
. В результате получается представление мног.
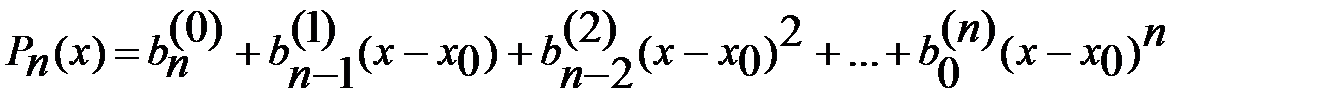. Сравнивая это выражение с разложением 
в ряд Тейлора в окр. точки 
: 
, получаем соотн. 
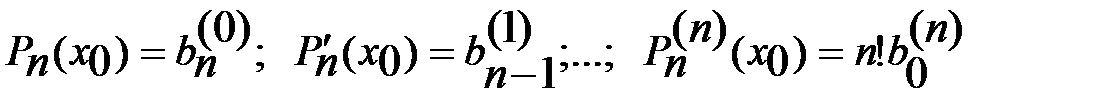. Т.е., используя рекуррентные соотн. (7), можно найти производные мног. 
в точке 
.